הבדלים בין גרסאות בדף "אינפי 1 לתיכוניסטים תש"ע"
(←שאלה) |
יהודה שמחה (שיחה | תרומות) |
||
| (241 גרסאות ביניים של 29 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | =אינפי 1 לתיכוניסטים= | + | =אינפי' 1 לתיכוניסטים= |
| + | כאן יהיה המקום שלנו להיעזר אחד בשני בקורס חשבון אינפיניטסימלי 1. אתם מוזמנים לשאול שאלות ולדון בבעיות הנוגעות לקורס אינפי' 1 - סטודנטים הלומדים בשתי הקבוצות מוזמנים להגיב כאן. | ||
| − | + | =ארכיון= | |
| + | [[אינפי 1 לתיכוניסטים תש"ע - ארכיון 1|ארכיון 1]] | ||
| − | + | [[אינפי 1 לתיכוניסטים תש"ע - ארכיון 2|ארכיון 2]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | - | + | |
| − | = | + | =תרגילי אתגר באינפי'= |
| − | * | + | *מצא סדרה כך שקבוצת הגבולות החלקיים שלה היא כל הממשיים |
| − | * | + | *מצא פונקציה רציפה בקטע <math>(0,1]</math> שאינה חסומה בו מלעיל ואינה חסומה בו מלרע |
| − | + | *מצא פונקציה מונוטונית שאינה רציפה באף סביבה של 0 | |
| + | *מצא פונקציה שאם תגזור אותה תקבל <math>\tan</math> | ||
| + | *הוכח/הפרך: הגבול של הסדרה <math>\sin(n)</math> אינו קיים | ||
| − | ==תרגיל | + | ===תרגיל אתגר מאתגר במיוחד=== |
| − | + | תרגילי האתגר הנ"ל מאתגרים וטריקיים אך ניתן לפתור אותם בעזרה הידע שלכם מקורס אינפי' בלבד. את האתגר הבא צריך לפתור בעזרת ידע מקורסים אחרים שלמדתם בנוסף: (קרדיט ללואי שפתרה את זה) | |
| − | + | *האם קיימת פונקציה מונוטונית שאינה רציפה באף נקודה בקטע <math>[0,1]</math> ? אם כן מצא אותה, אם לא הוכח שלא. | |
| − | + | ||
| − | + | (שוב, זה תרגיל מאד קשה, אל תרגישו רע אם אתם לא מצליחים לפתור אותו) | |
| − | + | ||
| − | === | + | ===פתרונות לאתגרים=== |
| − | + | '''[[פתרונות לאתגר אינפי 1 תיכוניסטים תש"ע|פתרונות]]''' | |
| − | == | + | =שאלות= |
| + | ==מהבוחן== | ||
| + | מישהו זוכר איך מראים שגבול הסדרה <math>\sqrt[n]{\sqrt[n]{n}-1}</math> הוא 1? כאשר (<math>\sqrt[n]{x}</math> זהו השורש ה- <math>n</math>-י של <math>x</math> . ובלינארית (מתוך מבחן של רון עדין), איך מראים שלמטריצות מתחלפות <math>A,B</math> (ז"א ש- <math>AB=BA</math>) קיים ו"ע משותף...? | ||
| − | + | ==שאלה== | |
| − | <math> | + | יש לי שאלה על גבול שאני מנסה למצוא אבל משום מה יש שלב אחד שלכאורה נראה לי נכון אבל הוא לא. נתונה הפונקציה: |
| − | + | :<math>\frac{p\sin(x)-\sin(px)}{x(\cos(x)-\cos(px))}</math> | |
| + | כאשר <math>x</math> שואף ל-0 | ||
| − | = | + | כאשר <math>p=\pi</math> . |
| − | + | ||
| − | + | פירקתי את השבר לשני שברים בצורה הבאה: כל מחובר של המונה לבדו עם המכנה (חיבור שברים עם אותו מכנה הוא שבר עם אותו מכנה כמו של השניים המקוריים כאשר מחברים את המונים שלהם, אם עדיין לא הבנת את כוונתי) | |
| + | ואז בצד אחד היה לי <math>\frac{\sin(x)}{x}</math> וזה שואף ל-1. בצד שני היה לי <math>\frac{\sin(px)}{x}</math> אז פשוט כפלתי וחילקתי ב- <math>p</math> ואז בגלל ש- <math>x</math> שואף ל-0, גם <math>px</math> שואף ל-0 מה שאומר שגם <math>\frac{\sin(px)}{px}</math> שואף ל-1. | ||
| + | |||
| + | ואז כביכול היה יוצא 0 כי שני השברים מצמצמים אחד את השני. | ||
| + | |||
| + | הבעיה היא במה שאמרתי על <math>\sin(px)</math> ו- <math>px</math> כי בדקתי במחשבון ושם זה נתן תוצאה אחרת. | ||
| + | |||
| + | לכן רציתי לדעת איך לפתור את זה באמת. | ||
| + | |||
| + | תודה | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | <math>\frac{\sin(px)}{px}\xrightarrow[x\to0]{}1</math> . קל לראות את זה לפי היינה. אם <math>x_n</math> סדרה ששואפת ל-0 אזי גם <math>\frac{x_n}{p}</math> סדרה ששואפת ל-0, פשוט תציב בפונקציה ותקבל שבזכות ש- <math>\frac{\sin(x)}{x}</math> שואף ל-1, שגם הפונקציה הזו על הסדרה הנ"ל שואפת ל-1. (לא ניסחתי מדויק, אני אשאיר לך לתקן את הפערים). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | מצטער אבל לא ממש הבנתי איך התשובה שלך קשורה לשאלה שלי. | |
| − | + | במחשבון יוצא שהפונ' שואפת ל-1.047 (וממש המספר הזה, לא 1) | |
| − | ( | + | אני אכתוב לך את מה שעשיתי ואני מקווה שתצליח להסביר לי מה היה לא נכון: |
| + | :<math>\lim\limits_{x\to0}\left[\frac{\pi\sin(x)-\sin(\pi x)}{x(\cos(x)-\cos(\pi x))}\right]</math> | ||
| − | + | זה שווה ל: | |
| + | :<math>\lim_{x\to0}\left[\frac{\pi\sin(x)}{x(\cos(x)-\cos(\pi x))}-\frac{\sin(\pi x)}{x(\cos(x)-\cos(\pi x))}\right]</math> | ||
| − | + | ששווה ל: | |
| + | :<math>\lim_{x\to0}\left[\frac{\pi}{\cos(x)-\cos(\pi x)}-\frac{\pi\sin(\pi x)}{\pi x(\cos(x)-\cos(\pi x))}\right]</math> | ||
| + | |||
| + | ששווה ל: | ||
| + | :<math>\lim_{x\to0}\left[\frac{\pi}{\cos(x)-\cos(\pi x)}-\frac{\pi}{(\cos(x)-\cos(\pi x))}\right]=0</math> | ||
| + | |||
| + | וזה אמור להיות 0 זהותית (כלומר ממש 0, לא שואף ל-0...) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | דבר ראשון, אסור בתכלית האיסור, להחליף באמצע התרגיל את חלק מהגבולות למספר אליו הם שואפים. אחרת <math>1^\infty</math> תמיד שווה 1 למרות שאנחנו יודעים שהוא יכול להיות e. ושוב, הייתי פותר את זה באמצעות כלל לופיטל, ולא בטוח איך אפשר אחרת. | |
| − | + | אוקי, אז נניח שהייתי מכניס את ה- <math>\lim</math> גם לשבר השני.. | |
| − | + | אני עדיין לא מבין למה זה לא היה עובד | |
| − | + | ||
| − | + | (ותודה שאתה ממשיך לענות לי למרות החפירה..) | |
| − | + | :מה הכוונה מכניס <math>\lim</math> לשבר השני? אסור לך להחליף במספר, אתה נשאר עם אינסוף פחות אינסוף ולא מצליח לחשב. לא יהיה לך זהותית 0. אסור לך למחוק את <math>\frac{\sin(x)}{x}</math> | |
| − | + | אז זה מה שאני לא מבין, למה אסור למחוק את <math>\frac{\sin(x)}{x}</math> הרי זה אמור להיות 1 כש- <math>x\to0</math> | |
| − | + | :כמו שאמרתי, לפי ההגיון הזה, גם <math>\left(1+\frac{1}{n}\right)^n=1</math> כי <math>1+\frac{1}{n}\to1</math> . במקרה זה, יש לך <math>1\cdot\infty-\infty</math> אסור להשתמש באריתמטיקה של גבולות במקרה זה. דוגמא נגדית פשוטה יותר: <math>\frac{n+1}{n}\cdot n-\frac{n-1}{n}\cdot n</math> בשיטה שלך זה 0 זהותית. במציאות, זה שווה בדיוק 2. | |
| − | + | הבנתי. תודה רבה! (וסליחה על החפירה הארוכה, שוב) | |
| − | ==שאלה | + | ==שאלה== |
| − | אם | + | רציתי לבדוק אם אני צודק: דורשים למצוא נקודות אי-רציפות וסיווגן בפונקציות הבאות: |
| − | + | 1) <math>\frac{\cos(x)}{|\cos(x)|}</math> | |
| − | + | ||
| + | 2) <math>\frac{e^{-\frac{1}{x^2}}}{2+\sin\left(\tfrac{2}{x}\right)}</math> | ||
| − | + | בשתיהן יצא לי 0 אי-רציפות סליקה. זה נכון? | |
| − | + | ||
| − | + | ===תשובה=== | |
| + | בראשון 0 '''אינה''' נקודת אי-רציפות בכלל... יש כמובן נקודות אי-רציפות אחרות, והן תמיד ממין ראשון. שים לב שהפונקציה הזו היא פשוט 1, 1- או לא מוגדרת. | ||
| − | |||
| − | |||
| − | == | + | בשני זה נכון, וזו אכן נקודת אי-הרציפות היחידה. |
| − | + | ||
| + | כן, בראשון התבלבלתי.. | ||
| + | תודה רבה! | ||
| + | |||
| + | ==שאלה== | ||
| + | אפשר בבקשה עזרה בתרגיל? צריך לבדוק האם <math>y=\cos\big(\log(x)\big)</math> רבמ"ש בקטע הפתוח <math>(0,-\infty)</math> . אני לא ממש רואה את זה... (אין גבול בשאיפה ל- <math>0^+</math> , אז ניסיתי להראות ע"י שתי סדרות שואפות ל-0 שאין רבמ"ש, לא ממש הולך לי...) | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | מה לא הולך? <math>x_n=e^{\pi-2\pi n}\ ,\ y_n=e^{-2\pi n}</math> . שתי הסדרות שואפות ל-0, ולכן המרחק ביניהן שואף ל-0. אבל הפונקציה עליהן שווה 1 או 1-. | |
| − | |||
| − | |||
| − | + | (זה לא כותב השאלה) אפשר פשוט לומר שהגבול באפס לא קיים, לכן הפונקציה לא רבמ"ש ב- <math>(0,1)</math> וכמובן שהיא לא רבמ"ש ב- <math>(0,\infty)</math> , לא? | |
| − | + | :(זה לא ארז) אני חושב שאסור, כי אז לפי מה שאתה אומר בגלל שלא קיים לsin x גבול באינסוף אז היא לא רבמ"ש... | |
| + | ::בכל מקרה, הדרך היחידה להוכיח שהגבול אינה קיים היא באמצעות הסדרות, כך שלא חסכת עבודה. באופן כללי, אפשר להוכיח שאם הגבול אינו קיים בצד הסופי, אזי הפונקציה לא רציפה שם במ"ש. זה נכון כי יש 2 אופציות: או שיש 2 סדרות ששואפות לצד הסופי (נגיד a) והפונקציה שואפת עליהן לגבולות שונים (וזה אוטומטית יוצר סתירה לרציפות במ"ש), או שיש סדרה ששואפת לאינסוף ואז הפונקציה אינה חסומה על קטע חסום, ולכן אינה רציפה במ"ש. אבל כמו שאמרתי, כך או כך זה דורש את בניית הסדרות. | ||
| − | = | + | :לאדע, לא עולה לי כל כך מהר הדוגמאות להפרכה. תודה בכל מקרה! יש לי עוד שאלה ממש קטנה, אני מנסה להוכיח שכשX שואף ל0, אז ln sin x / ln x שואף ל1. |
| + | :האם מותר לי להגיע לזה באמצעות המשפט של sin x / x =1 ? כי אז אני מכפיל בX, מפעיל LN על שני האגפים, מחלק בLN X ומקבל את הדרוש... תודה לעונה! | ||
| + | אסור. אין משפט שsinx/x=1 יש משפט שאומר שזה שואף לאחד... אבל לכפול בx זה כמו לכפול באפס וזה בוודאי אסור (אריתמטיקה של גבולות לא עוזרת פה). אפשר לפתור באמצעות כלל לופיטל, כמו שאמרתי אני לא יודע אם זה בחומר או לא. | ||
| − | לא | + | זה לא בחומר, תודה בכל מקרה.! |
| − | == | + | ==שאלה== |
| + | יש משהו שנורא מבלבל אותי. | ||
| + | נניח שיש לי את הפונקציה: <math>f(x)=e^{lnx}</math> | ||
| − | + | מצד אחד הנגזרת שלה היא 1, כי היא שווה ל-X | |
| − | + | ||
| − | + | מצד שני, אם אני מתעלם מהעובדה שהדבר הזה הוא X ואני גוזר רגיל אני מקבל שהגזרת היא 1 חלקי X. | |
| − | + | מה עושים??? | |
| − | + | דרך אגב, ארז כתבתי לך בחזרה משהו בשאלה של ה- <math>\lim_{x\rightarrow 0}\frac{sin(\pi x)}{\pi x}</math> | |
| − | + | אז בבקשה תענה לי. | |
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | לומדים לגזור! | |
| − | ' | + | <math>[e^{lnx}]' =e^{lnx} \cdot \frac{1}{x}=\frac{x}{x}=1</math> |
| − | ==שאלה== | + | חח אופס, סליחה. |
| − | + | ||
| + | ==שאלה - רבמ"ש== | ||
| + | נכון, חפרנו על הנושא למרות שתהיה מקסימום שאלה אחת על זה במבחן, ובכל זאת: | ||
| + | נניח שאני רוצה להוכיח ש- f(x)=xsinx רבמ"ש. האם מותר לי לקחת x,y שמקיימים <math>|x-y|<d</math> ולומר : | ||
| + | <math> | ||
| + | |xsinx-ysiny| \le |2x-2y| < 2d | ||
| + | </math> | ||
| + | (מהסיבה שפונק' הסינוס חסומה ע"י 1 ו-1-) ? | ||
===תשובה=== | ===תשובה=== | ||
| − | + | בוודאי שלא. למשל <math>x=2000\pi, y=2000\pi + \pi/2, d = \pi/2</math> אז יוצא ש<math>|xsinx-ysiny|= 2000\pi + \pi/2</math> | |
| − | |||
| − | + | הטריק הוא בגדול לקחת <math>x_1=x,x_2=x+h</math> ולפתח לפי נוסחאות טריגונומטריות. | |
| + | ==שאלה - טורים== | ||
| + | ישבתי על זה הרבה ולא הצלחתי X: | ||
| + | :נתון שיש טור המוגדר ע"י סכום הסדרה an ובדומה סכום המוגדר ע"י סכום הסדרה bn | ||
| + | :ידוע שסיגמא AN זה A וסיגמא BN זה B | ||
| + | :מגדירים סדרה חדשה, CN שבמקומות האי זוגיים היא מקבלת את b1,b3,b5.... ובמקומות הזוגיים היא מקבלת את a1,a2,a3,... | ||
| + | :האם סיגמא CN מתכנס? | ||
| − | + | ===תשובה=== | |
| + | לא של ארז: | ||
| + | מקווה שזה נכון: | ||
| + | סכום האי זוגיים של הסדרה b מתכנס לפי קריטריון ההשוואה, הסכום של a כמובן מתכנס לפני הנתון | ||
| + | ולכן סכום טורים מתכנסים הוא מתכנס. | ||
| + | |||
| + | |||
| + | :מבחן ההשוואה נכון לטורים חיוביים בלבד. והתשובה היא בוודאי לא, אם לא נתון שהטורים חיוביים. לוקחים את הטור הקלאסי להתכנסות בתנאי <math>b_n=(-1)^n/n</math> ולוקחים כל טור מתכנס אחר להיות a_n... | ||
==שאלה== | ==שאלה== | ||
| − | + | שאלה מהמבחן של ראובן שנה שעברה שלא הצלחתי: | |
| − | + | ||
| − | + | ||
| − | + | תהי an סדרה מתכנסת כך ש: <math>s={an: n - belong - to - N}</math> כאשר N זה המספרים הטבעיים. ואומרים ש-s היא קבוצה סופית. | |
| − | + | צריך להוכיח שהחל מ-N מסויים, לכל n,m שגדולים ממנו, an=am. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | זה נראה לי נכון אבל אני לא יודע איך לכתוב את זה בצורה מתמטית. | ||
| + | ===תשובה=== | ||
| − | + | S הינה קבוצת כל האיברים בסדרה, והיא סופית. כלומר איבר בסדרה יכול להיות אחד מתוך מספר סופי של איברים (איבר מתוך S). | |
| − | + | ||
| − | == | + | כעת, נגדיר את קבוצת ההפרשים <math>D=\{|s_1-s_2| : s_1,s_2 \in S, s_1\neq s_2\}</math> מכיוון שS סופית גם D סופית ולכן יש לה מינימום. נגדיר <math>\epsilon = Min(D)/2>0</math>. כעת, לפי תנאי קושי, קיים <math>n_0</math> כך שלכל <math>n,m>n_0</math> מתקיים <math>|a_m-a_n| < \epsilon</math> |
| − | + | אבל אם <math>a_n \neq a_m </math> אזי <math>|a_m-a_n| \in D</math> אבל | |
| + | |||
| + | <math>|a_n-a_m|<\epsilon < Min(d)</math> וזו סתירה. | ||
| + | |||
| + | :סבבה תודה! | ||
| + | |||
| + | |||
| + | ===מבחן של ראובן=== | ||
| + | איפה יש את המבחן שלו משנה שעברה? | ||
| + | |||
| + | באתר של גיל | ||
| + | |||
| + | איפה זה, אפשר קישור? | ||
| + | |||
| + | http://math.ipnet.co.il | ||
| + | |||
| + | תודה | ||
==שאלה== | ==שאלה== | ||
| − | + | באחת משאלות האתגר שנתתם (זאת עם הגבולות החלקיים שכוללים את כל הממשיים), מותר לי פשוט להגיד ש-an היא הספירה של Q? | |
| − | + | אנחנו יודעים שאפשר לספור את Q אבל האם זה מספיק להסתמך על זה שקיימת ספירה כזאת ואז לרשום שנק' ההצטברות של Q הן כל R ולכן אלו הם הג"חים? | |
| − | == | + | ===תשובה=== |
| − | + | השאלה היא האם משם אתה יכול להוכיח שכל מספר ממשי הוא גבול חלקי של הסדרה הנ"ל. אין משפט על הקשר שבין נקודת הצטברות של קבוצה, לבין הגבולות החלקיים של סדרה המכילה את איברי הקבוצה. האם הסדר לפי תבנה את הסדרה משנה? | |
| − | + | :אוקיי.. יש לי סדרה אחרת שנראה לי שהיא תעבוד. את כל שאר תרגילי האתגר הצלחתי לפתור (חוץ מזה שדורש שימוש בקורס אחר שאין לי מושג מה לעשות שם חוץ מזה שאני בטוח כמעט לגמרי שזו הפרכה..) | |
| − | + | ||
| − | + | ::תשלח לי למייל בקצרה, אני אגיד לך אם צדקת. אגב, מתי המבחן שלכם? | |
| − | + | :::המבחן שלנו מחר :S | |
| − | + | ||
| + | ::::הא, בהצלחה.. יכול להיות שאני אהיה מחר באוניברסיטה.. אבל זה כבר לא יעזור לאף אחד :) | ||
| + | |||
| + | ==שאלה== | ||
| + | הוכח שאם f גזירה ב-(a,b), ונגזרתה חסומה בקטע, אזי f רבמ"ש שם. | ||
| + | (WTF?!) | ||
===תשובה=== | ===תשובה=== | ||
| − | + | נניח בשלילה שהיא אינה רציפה במ"ש, לכן קיים אפסילון, כך שלכל דלתא קיים זוג x,y כך שהמרחק בינהם קטן מדלתא, אבל המרחק בין f(x) לf(y) גדול מאפסילון. ולכן <math>\frac{f(x)-f(y)}{x-y} > \frac{\epsilon}{\delta}</math>. ניקח <math>\delta_n = \frac{1}{n}</math> וניקח את הזוגות המתאימים <math>x_n,y_n</math>. אלה סדרות חסומות ולכן ניתן לקחת תת סדרה של <math>x_n</math> שמתכנסת, ואז תת-תת סדרה של y_n שמתכנסת וביחד נקבל שתי סדרות מתכנסות <math>x_{n_k},y_{n_k}</math> ומכיוון שהמרחק ביניהן הולך וקטן הן מתכנסות לאותו הגבול, נקרא לו L. אבל אז | |
| − | + | <math>\frac{f(x_{n_k})-f(y_{n_k})}{|x_{n_k}-y_{n_k}|} > \frac{\epsilon}{\delta_{n_k}}</math> כלומר שואף לאינסוף, אבל זה חסום על ידי קבוע כפול הנגזרת (לפי תרגיל אחר שנתנו לכם) וזו סתירה. | |
| + | :: אתה יכול בבקשה להסביר למה הכוונה ב"זוגות המתאימים Xn Yn" - הכוונה היא לאותן סדרות שעזרו לך להוכיח או להפריך משהו בהרבה תרגילים אחרים בעמוד זה? | ||
| + | :: ועוד משהו, למה הכוונה חסום ע"י קבוע כפול הנגזרת? | ||
| + | |||
| + | |||
| + | "... כך שלכל דלתא קיים זוג x,y..." הזוג הזה. | ||
| + | |||
| + | חסום ע"י הכוונה "קטן מ.." | ||
==שאלה== | ==שאלה== | ||
| − | + | נניח שאנחנו מקבלים פונקצייה כמו: | |
| − | ( | + | <math>cos\frac{1}{ln(x^2)}</math> . האם מצפים מאתנו להתייחס אליה כמוגדרת גם ב-x<0 (כפי שהיא כתובה), או ללכת צעד אחד קדימה ולהפוך את זה ל: <math>cos\frac{1}{2lnx}</math> ? |
| − | + | שאלה נוספת - כדי להוכיח שלא קיים גבול בנק' x=1, במקרה זה, האם מותר לי להשתמש בנימוק המילולי הבא (?): הפונקצייה מבצעת אינסוף מחזורים בכל סביבה של x=1, לכן הגבול לא קיים. | |
| + | אם לא, איך אחרת אפשר לנמק את אי-קיום הגבול בנק', בלי פשוט לומר שהפונק' שבתוך ה-cos שואפת לאינסוף? | ||
| − | |||
| − | == | + | ===תשובה=== |
| − | + | כמובן שהיא מוגדרת באפס. לא עושים שום צעדים קדימה או אחורה. זה כמו שx/x אינה מוגדרת באפס. | |
| − | + | ||
| + | לא, תקרא את הדוגמאות האחרות (כמעט זהות) בנושא. בונים 2 סדרות ששואפות ל1 אבל הפונקציה עליהן הולכת לפלוס אחד או מינוס אחד ולכן אין גבול לפי היינה. | ||
| + | |||
| + | ==שאלה== | ||
| + | האם זהו משפט נכון? M = SUP A אם"ם לכל e>0 קיים a ששייך לA כך ש M-e<a | ||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | |||
| − | + | לא מדוייק | |
| − | + | M=supA אם"ם '''M חסם עליון''' וגם e>0 קיים a ששייך לA כך ש M-e<a | |
| − | + | M חסם עליון אומר M גדול מכל האיברים בקבוצה, והתנאי עם האפסילון נותן את המינימליות של M. אם הוא לא היה מתקיים, אז M-e היה חסם עליון קטן יותר. | |
| − | ==שאלה | + | ==שאלה== |
| − | + | האם הפו' 1 חלקי n רציפה בקטע [0,1) ? ורבמ"ש? | |
===תשובה=== | ===תשובה=== | ||
| − | + | רציפה שם, ברור, זה פונקציה רציפה חלקי רציפה, כאשר הפונקצה במכנה שונה מאפס. | |
| + | היא אינה רציפה שם במ"ש כי היא אינה חסומה שם. ופונקציה שרציפה במ"ש על קטע <s>סגור</s> חסומה בו. | ||
| + | :אבל זה לא קטע סגור, הוא חצי פתוח O: | ||
| + | ::שגיאה שלי, הכוונה הייתה לקטע '''חסום''' ולא סגור. פונקציה רציפה במ"ש על קטע '''חסום''' חסומה בו. | ||
| + | :::זאת אומרת שהפעם היחידה שאנחנו צריכים ממש להפריך את הרבמ"ש שלא ע"י משפט, זה כשהיא רציפה והגבול באינסוף או מינוס אינסוף אינו קיים? | ||
| + | ::::לא. לפני שנייה הייתה דוגמא של coslogx | ||
| − | + | תודה רבה :) | |
| − | + | ||
| − | + | ==הוכחת משפט ערך הביניים== | |
| + | במייזלר יש הוכחה שמשתמשת בטענת עזר שקשורה בחיתוך עם ציר ה-x של הפונקצייה. למה לא לפשט את זה להוכחה כזו (האם היא תקינה?): | ||
| + | תהי f רציפה ב-[a,b], אזי אם <math>f(a)<y<f(b)</math> נבנה סדרת קטעים <math>I_n=[a_n,b_n]</math> כך ש- <math>f(a_n) \le y \le f(b_n)</math> , כאשר <math>I_1=[a,b], I_n=[a_n,b_n]</math>, ו-<math>c_n</math> מוגדרת: <math>c_n=0.5(a_n+b_n)</math>, כך שאם <math>f(c_n)\le y</math> נגדיר <math>I_{n+1}=[c_n,b_n]</math>, ואחרת <math>I_{n+1}=[a_n,c_n]</math> . לפי קנטור קיימת נק' יחידה <math>x_0</math> באמצע כך ש- <math>lim(a_n)=lim(b_n)=x_0</math> , ובגלל הרציפות של f נקבל ש- <math>f(a_n)</math> ו- <math>f(b_n)</math> שואפים להיות y. | ||
| + | |||
| + | ===תשובה=== | ||
| + | זו הוכחה נכונה, אמנם חסרת כמה פרטים, אבל נכונה. | ||
==שאלה== | ==שאלה== | ||
| − | ארז | + | ארז באחת השאלות למעלה אמרת: |
| + | "אפשר להוכיח שאם הגבול אינו קיים בצד הסופי, אזי הפונקציה לא רציפה שם במ"ש." | ||
| − | + | אבל כפי שמישהו מעלייך אמר, אז sin רציפה במידה שווה בכל R ואין לה גבול באין-סוף | |
| − | + | :באיזה מובן אינסוף הינו "צד סופי"?? | |
| − | + | ||
| − | + | ::אופס, הלחץ מהמבחן עושה את שלו.. | |
| − | + | ||
| − | : | + | :: אם כבר הגענו לנושא הזה: |
| + | :: א) אין אריתמטיקה בין פונקציות רבמ"ש נכון?, לדוגמא כפל פונ' שהן רבמ"ש (נגיד בקטע [a,b]) לא יהיה בהכרח רבמ"ש נכון? | ||
| + | :: ב) איך מוכיחים ש-sin רבמ"ש ע"פ הגדרה (בלשון דלתא ואפסילון)? (מה הטריק השם, איזה איקסים לוקחים?) | ||
| − | |||
| − | |||
| − | = | + | ===תשובה=== |
| − | + | א. יש חצי אריתמטיקה. כפל אין (x כפול x) אבל חיבור יש כמובן. בנוסף יש הרכבה, הרכבה של רציפות במ"ש הינה רציפה במ"ש | |
| − | + | ב. תרגיל כללי הוא להוכיח שכל פונקציה שרציפה על כל הממשיים ומחזורית הינה רציפה במ"ש. סינוס זה מקרה פרטי של המשפט הגדול הזה. בצורה דומה <math>e^{(sinx)^2}</math> הינה רציפה במ"ש למשל.. | |
| − | + | ||
| + | :: ב-ב' זה בגלל ש-sin רציפה בקטע סגור, ואז היא רבמ"ש בו, ובעצם בגלל שהיא מחזורית אז זה מעיין איחוד אין סופי של אותו הקטע נכון? | ||
| − | + | ובדוגמא שנתת - איך מוכיחים שהפונ' הזאת מחזורית? | |
| + | |||
| + | |||
| + | :::לכל פונקציה מחזורית זה נכון. צ"ל להוכיח את זה במדויק, אבל מה שציינת זו אכן הדרך. | ||
| + | ::: פשוט מציבים <math>x+2\pi k</math> ורואים מיידים שזה שווה לערך של x לכל x | ||
| + | |||
| + | ::::אוקי, תודה :) | ||
| + | ==שאלה== | ||
| + | שני דברים: | ||
| + | א) צריך להוכיח במבחן שפונקציה רציפה ומחזורית היא רבמ"ש בכל פעם שמסתמכים על זה? אפשר לתת כאן הוכחה ליתר ביטחון? | ||
| + | ב) ארז, אתה יכול להעלות פתרונות לשאלות אתגר? מחר (חמישי) המבחן ומעניין אותי לדעת איך לפתור את השאלה שקשורה לקורסים אחרים... | ||
===תשובה=== | ===תשובה=== | ||
| − | + | אני לא יודע על מה מותר או אסור לכם להסתמך. אבל ההוכחה הולכת ככה: אתה מחלק את כל הממשיים לקטעים באורך המחזוריות, על כל קטע סגור וחסום הפונקציה רציפה במ"ש. עכשיו, כל שתי נקודות מספיק קרובות יכולות להיות במצב אחד מבין שניים: או ששתיהן באותו קטע, או שהן בקטעים חופפים. לכן נחלק גם את הממשיים לקטעים באורך פעמיים המחזוריות, וגם שם הפונקציה רציפה במ"ש. ולכן ניקח את הדלתא המינימלי בין זה של פעמים הקטע וזה של הקטע, וכל שתי נקודות שקרובות עד כדי הדלתא הזה, יהיה קרובות עד כדי האפסילון. | |
| − | + | אני אשתדל להעלות פתרונות, לא בטוח שאני אספיק מלאים, אבל לפחות אני אתן את העיקר | |
| − | =שאלה= | + | == שאלה == |
| − | + | ארז איך מוכיחים ש <math>\frac{x}{e^x+1}</math> רבמ"ש? | |
| + | :היא לא רבמ"ש, אמנם כשהיא שואפת לאינסוף יש לה גבול והוא 0, אבל כשתשאיף אותה למינוס אינסוף היא תשאף למינוס אינסוף. | ||
| + | ::המשפט בבדיקת אינסוף ומינוס אינסוף הוא לא אם"ם, אלא רק כיוון אחד. היא אפילו כן רבמ"ש, כי היא רבמ"ש בצד החיובי של ציר הx, ובצד השלילי הוא מתנהג כמו x שהוא לינארי ולכן רבמ"ש. (לא הוכחה פורמלית) | ||
| + | :::אפשר בבקשה הוכחה פורמלית | ||
| + | ::::צודק ברעיון של הבדיקה של האינסוף, אבל לא הבנתי למה אתה אומר שבצד השלילי הוא מתנהג כמו x לינארי - הוא הרי שואף למינוס אינסוף בצורה קיצונית, יותר מהר מכל פונקצייה אחרת (אם לא הייתי יודע שזה מוגדר הייתי בטוח שזו אסימפטוטה). | ||
| + | :::::לא, כי במינוס אינסוף המכנה שואף ל1 והמונה הוא x. כלומר ככל שהוא מתקרב למינוס אינסוף, הוא מתקרב (שואף) לx. | ||
| + | :::::בנוסף, ההוכחה הפורמלית רק אפשרית ישירות מההגדרה עם אפסילון ודלטא. | ||
| + | :::::: רגע, אז אפשר לחלק את זה לשני קטעים אפס עד איןסוף ומינוס אינסוף עד אפס ולהגיד שבראשון היא רציפה במ"ש בגלל גבולות בקצוות, ובשני היא מתנהגת כמו הגרף של X, ואז רק נותר להראות מה קורה אם לוקחים X1 מקטע אחד ו-X2 מהקטע השני? | ||
| + | :::::::בעקרון כן, אבל זה לא כל כך פורמלי. הכל מסתמך על זה שאם פונקציה רבמ"ש בשתי קטעים אז היא רבמ"ש באיחוד שלהם. זה נראה נכון הגיונית, אבל אני לא בטוח שמותר להשתמש בזה במבחן. | ||
| + | ::::::::אבל בגלל זה אמרתי שרק צריך לבדוק מה קורה אם X1 מהקע הראשון וX2 מהקטע השני -זאת הבדיקה של האיחוד. אבל האם יש "מבחן השוואה" לרציפות במ"ש? כי אם לא אז איך אני יכול להגיד שמתחת ל-0 הפונ' מתנהגת כמו X? הרי היא מתנהגת בין X/2 ל-X (אמנם שתיהן רציפות, אבל בגלל זה שאלתי על מבחן ההשוואה)... | ||
| − | + | ::::::::: (מישהו אחר) ארז קראתי את מה שנכתב פה, אתה יכול להגיד בקצרה מהי הדרך לומר שזה אכן רבמ"ש (או להפריך את זה..)? | |
| + | :::::::::: אני לא ארז, אבל שוב: אפשר להוכיח ישירות לפי הגדרה עם אפסילון ודלטא. | ||
| − | + | ::::::::::: אני שוב לא בטוח איך הכוונה לפתור את השאלה, כי יש דרכים בעזרת נגזרות (כמו ששאלו באתר, אם הנגזרת חסומה הפונקציה רציפה במ"ש) אבל לא למדנו את המשפטים האלה, לכן אני לא יודע מאיפה השאלה ובאיזה שיטה צריך לפתור... | |
| − | + | ||
| − | + | == תודה! == | |
| + | ארז, אמרנו את זה כבר בלינארית, אבל אתה ממש בן אדם מדהים! לא הייתי מצפה מהמתרגל הכי טוב שיעזור לקבוצה בקורס שהוא לא מלמד, ובטח ובטח לא בכל כך מסירות! תודה רבה על כל העזרה והתמיכה (והאתגרים :P) והלימוד המצויין! בבקשה תתרגל אותנו אינפי 2! אין לי (ולכולנו) מילים להודות לך! | ||
| − | + | איך להגיד את זה שיינר, אם היית וקטור, לא היה אפשר לנרמל אותך כי אתה פשוט לא נורמלי! | |
| + | אם היית פונקציה, היית שואף לאינסוף בכל סביבה של כל נקודה | ||
| + | אם היית קטע, היית כל הישר. | ||
| − | + | אם היית מצחיק אחי אולי ההיתי צוחק | |
| + | *ואם לא היה לך כזה קטן אולי לא היית צריך לרדת על אחרים בשביל לצאת גבר, אחי ;) | ||
| + | בוא בוא תסביר את עצמך כי וואלה לא הבנתי .. | ||
| + | *עזוב, עזוב, אי הבנה, זה הכל | ||
| − | + | :: ארז כל הכבוד! אבסורד שאתה המתרגל שהכי עזר לנו בקורס הזה | |
| − | + | :: אני גם מעדיף שתתרגל אותנו באינפי 2 | |
| − | + | :: בסופו של דבר הוא כן מתרגל (של קבוצה א') :) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | == | + | == הכרזה == |
| − | + | יש ציונים!!! | |
| − | |||
| − | |||
| − | + | == שאלה ברציפות במידה שווה == | |
| + | שלום, רציתי הוכחה בבקשה לתרגיל ברציפות במידה שווה. | ||
| − | + | האם איקס כפול סינוס איקס, רציפה במ"ש בקטע בין מינוס אינסוף לאינסוף.. | |
| − | האם | + | |
| + | תודה רבה!! | ||
===תשובה=== | ===תשובה=== | ||
| − | + | קח 2 סדרות | |
| + | <math>x_n = 2\pi n</math> ו <math>y_n = \frac{1}{n} + 2\pi n</math>. ברור שההפרש בינהן שואף לאפס, אבל <math>f(y_n) - f(x_n) = (\frac{1}{n} + 2\pi n)sin(\frac{1}{n})</math> אבל הביטוי הזה שואף ל<math>2\pi</math> ולכן בוודאי גדול מקבוע שגדול מאפס (למשל אחד) החל משלב מסויים... | ||
| − | + | ::תודה רבה ארז! אתה תותח! | |
| − | ==שאלה== | + | == שאלה בקשר למשפט על רציפות במידה שווה == |
| − | + | קראתי כאן וגם בהרצאה משפט שמדבר על: | |
| + | פונקציה שרציפה בקטע (a,b) (כאשר a ,b או שניהם הם אינסוף או מינוס אינסוף), אז אם הגבולות בהם קיימים וסופיים, הפונקציה רציפה במידה שווה. | ||
| + | אם יש לי קטע פתוח בין 0 לאינסוף, ופונקציה של (סינוס של איקס) חלקי איקס בריבוע, ראיתי שהוא בודק את הגבולות באינסוף וב0 מימין, אבל בדוגמא אחרת, של סינוס של אחד חלקי איקס, בין אחד לאינסוף, הוא בדק רק את הגבול כשאיקס שואף לאינסוף. | ||
| + | למה הוא לא בדק את הגבול כשאיקס שואף לאחד מימין? כי הפונקציה מוגדרת באחד ולכן לא צריך לבדוק את זה? (ולעומת זאת בדוגמא הראשונה, כשאיקס שווה לאפס אז זה תחום ההגדרה ולכן צריך כן לבדוק?). | ||
| + | ושאלה אחרונה בקשר למשפט שאמרתי, בהרצאה הוא לא ציין שa או b חייבים להיות אינסוף, האם זה נכון גם כשהם מספרים ממשיים? | ||
| + | תודה רבה!! | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | <math>sin(1/x)</math> רציפה באחד ולכן ברור שהגבול שם קיים ואין צורך בבדיקה נוספת. כאשר היא לא רציפה (מסיבה של תחום הגדרה או כל סיבה אחרת, אז יש לבדוק מה הגבול. | |
| − | + | ||
| − | + | ||
| − | + | כן, כי אם f רציפה בקטע הפתוח (a,b) ויש לה גבולות חד צדדים בקצות הקטע, אזי '''לפי הגדרה''' f רציפה בקטע הסגור [a,b]. ואז '''לפי משפט''' f רציפה בו במ"ש. | |
| − | : | + | * הבנתי לגמרי עכשיו, תודה ענקית!! :] |
| − | + | == שאלה בנושא רציפות במידה שווה == | |
| − | + | רציתי לדעת בבקשה איך מוכיחים שהפונקציה קוסינוס של שורש של ערך מוחלט של X רציפה במידה שווה בR. אולי להפריד ל2 מקרים כשX>0 וכשX<0.. תודה רבה!!!! | |
| − | + | ||
| − | < | + | |
| − | + | ===תשובה=== | |
| + | כן להפריד למקרים, ואז זו הרכבה של רציפות במ"ש. את שורש איקס אפשר להוכיח לפי ההגדרה באמצעת כפל בצמוד. | ||
| + | |||
| + | * הבנתי, תודה שוב ושיהיה לך לילה טוב.. | ||
| + | |||
| + | == משפט הערך הממוצע == | ||
| + | שלום, רציתי לדעת בבקשה אם נלמד משפט הערך הממוצע בכיתה..? תודה רבה :] | ||
===תשובה=== | ===תשובה=== | ||
| − | + | בהתחשב בעובדה שאינפי 2 כבר התחיל ובמסגרתו למדנו המשפט הזה, השאלה הזו קצת מפתיעה. | |
| − | + | משפט הערך הממוצע הינו משפט לגרנז' ולמדנו אותו בתחילת סימסטר ב' (ולא כחלק מסמיסטר א'...) | |
| + | * לא הסברתי טוב, אני יודע שהוא נלמד, השאלה אם הוא יכול להיות במבחן מועד ב' באינפי 1 אבל הבנתי שלא.. תודה על התשובה.. | ||
| − | |||
| − | + | == תרגיל ברציפות במידה שווה == | |
| + | שלום ארז, יש לי תרגיל שלא הצלחתי לפתור ואני ישמח אם תעזור לי | ||
| + | לבדוק רציפות במידה שווה של (x*cos(1/x^2 בקטע שבין (אינסוף, 0). | ||
| + | לעניות דעתי צריך להפריך. | ||
| + | ועוד שאלה קטנה בקשר להפרכה: צריך לקחת שתי סדרות כך שאחד התנאים הוא שהחיסור ביניהן כשמשאיפים לאינסוף ישאף ל-0. אם הוא שווה ל-0 ולא שואף ל-0, האם התנאי הזה התקיים? (כמובן שצריך לבדוק מה קורה כשמציבים את הסדרות בפונקציה אך אני מדבר רק על התנאי הראשון). | ||
| + | אודה לך על תשובתך! | ||
| − | |||
| − | |||
| − | + | ===תשובה=== | |
| + | אם החיסור בינהן שווה אפס אז זה אותה סדרה, ואז בוודאי שהתנאי על כך שההפרש בין הפונקציות מופעלות על הסדרות צריך להיות גדול מקבוע, לא יתקיים. | ||
| − | + | ודווקא נראה לי שצריך להוכיח, כי הנגזרת חסומה. אני אנסה לפתור את זה מחר. | |
| + | = תודה מקרב לב | ||
| − | + | ==2 הגדרות ו2 שאלות ברבמ"ש== | |
| + | היי ארז מה נשמע? יש לי בבקשה כמה שאלות.. | ||
| − | : | + | 1) בהגדרת היינה בורל במבחן, מספיק לרשום: "S קומפקטית אם ורק אם היא חסומה וסגורה", זה מספיק או שצריך להסביר גם מה זה קומפקטית..? |
| − | + | 2) אם יש שאלה לנסח את משפט בולצ'אנו ויירשטראס, איזה מהם? עבור סדרות, קבוצות או פונקציות? או מה שאני בוחר? | |
| − | + | 3) רבמ"ש: איקס כפול קוסינוס של איקס בין מינוס אינסוף לאינסוף.. (בטח להפריך) | |
| − | + | 4) רבמ"ש: איקס כפול לוג של איקס בין אפס לאינסוף (לפי דעתי צריך להפריך כי מבחינת אינטואיציה, לוג איקס שואף ממינוס אינסוף ואם נכפיל באיקס אז זה עוד יותר מינוס אינסוף..) | |
| + | |||
| + | אלה השאלות האחרונות שאני אשאל.. מקווה שיהיה לך זמן.. תודה רבה רבה רבה, אם נצליח זה רק בזכותך תאמין לי.. ואם להגיד את האמת אז חבל שלא הבנתי את זה בתחילת סמסטר א', העיקר שעכשיו אני מבין.. תודה שוב :] | ||
===תשובה=== | ===תשובה=== | ||
| − | + | 1,2 אלה שאלות למרצה. | |
| + | 3. זה בדיוק כמו xsinx שעניתי עליו | ||
| + | |||
| + | 4. זה להפריך, אפשר עם שתי הסדרות <math>n + \frac{1}{n}</math> ו <math>n</math>. צריך לשחק קצת עם הlog ובעיקר לשים לב שזו הפונקציה <math>xlogx = log(x^x)</math> וההפרש בין שני לוגים הוא לוג של החלוקה. | ||
| + | * * תודה רבה!! אני אנסה את מה שאמרת.. שיהיה בהצלחה לכל מי שניגש.. וארז, תודה על הכל!! | ||
| + | |||
| + | |||
| + | ==שאלה== | ||
| + | במועד ב' באינפי 1, ניתן להשתמש בכלל לופיטל? | ||
| − | + | לא בטוח באיזה קורס, אבל אם לא למדתם את זה באינפי 1 לא ניתן להשתמש בזה במבחן | |
גרסה אחרונה מ־11:06, 22 בספטמבר 2016
תוכן עניינים
- 1 אינפי' 1 לתיכוניסטים
- 2 ארכיון
- 3 תרגילי אתגר באינפי'
- 4 שאלות
- 4.1 מהבוחן
- 4.2 שאלה
- 4.3 שאלה
- 4.4 שאלה
- 4.5 שאלה
- 4.6 שאלה - רבמ"ש
- 4.7 שאלה - טורים
- 4.8 שאלה
- 4.9 שאלה
- 4.10 שאלה
- 4.11 שאלה
- 4.12 שאלה
- 4.13 שאלה
- 4.14 הוכחת משפט ערך הביניים
- 4.15 שאלה
- 4.16 שאלה
- 4.17 שאלה
- 4.18 תודה!
- 4.19 הכרזה
- 4.20 שאלה ברציפות במידה שווה
- 4.21 שאלה בקשר למשפט על רציפות במידה שווה
- 4.22 שאלה בנושא רציפות במידה שווה
- 4.23 משפט הערך הממוצע
- 4.24 תרגיל ברציפות במידה שווה
- 4.25 2 הגדרות ו2 שאלות ברבמ"ש
- 4.26 שאלה
אינפי' 1 לתיכוניסטים
כאן יהיה המקום שלנו להיעזר אחד בשני בקורס חשבון אינפיניטסימלי 1. אתם מוזמנים לשאול שאלות ולדון בבעיות הנוגעות לקורס אינפי' 1 - סטודנטים הלומדים בשתי הקבוצות מוזמנים להגיב כאן.
ארכיון
תרגילי אתגר באינפי'
- מצא סדרה כך שקבוצת הגבולות החלקיים שלה היא כל הממשיים
- מצא פונקציה רציפה בקטע
![(0,1]](/images/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) שאינה חסומה בו מלעיל ואינה חסומה בו מלרע
שאינה חסומה בו מלעיל ואינה חסומה בו מלרע - מצא פונקציה מונוטונית שאינה רציפה באף סביבה של 0
- מצא פונקציה שאם תגזור אותה תקבל
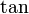
- הוכח/הפרך: הגבול של הסדרה
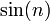 אינו קיים
אינו קיים
תרגיל אתגר מאתגר במיוחד
תרגילי האתגר הנ"ל מאתגרים וטריקיים אך ניתן לפתור אותם בעזרה הידע שלכם מקורס אינפי' בלבד. את האתגר הבא צריך לפתור בעזרת ידע מקורסים אחרים שלמדתם בנוסף: (קרדיט ללואי שפתרה את זה)
- האם קיימת פונקציה מונוטונית שאינה רציפה באף נקודה בקטע
![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) ? אם כן מצא אותה, אם לא הוכח שלא.
? אם כן מצא אותה, אם לא הוכח שלא.
(שוב, זה תרגיל מאד קשה, אל תרגישו רע אם אתם לא מצליחים לפתור אותו)
פתרונות לאתגרים
שאלות
מהבוחן
מישהו זוכר איך מראים שגבול הסדרה ![\sqrt[n]{\sqrt[n]{n}-1}](/images/math/2/c/1/2c1c3f1c9ef7ad55c60a7b1f2b8eea55.png) הוא 1? כאשר (
הוא 1? כאשר (![\sqrt[n]{x}](/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) זהו השורש ה-
זהו השורש ה-  -י של
-י של  . ובלינארית (מתוך מבחן של רון עדין), איך מראים שלמטריצות מתחלפות
. ובלינארית (מתוך מבחן של רון עדין), איך מראים שלמטריצות מתחלפות 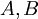 (ז"א ש-
(ז"א ש- 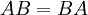 ) קיים ו"ע משותף...?
) קיים ו"ע משותף...?
שאלה
יש לי שאלה על גבול שאני מנסה למצוא אבל משום מה יש שלב אחד שלכאורה נראה לי נכון אבל הוא לא. נתונה הפונקציה:
כאשר  שואף ל-0
שואף ל-0
כאשר 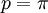 .
.
פירקתי את השבר לשני שברים בצורה הבאה: כל מחובר של המונה לבדו עם המכנה (חיבור שברים עם אותו מכנה הוא שבר עם אותו מכנה כמו של השניים המקוריים כאשר מחברים את המונים שלהם, אם עדיין לא הבנת את כוונתי)
ואז בצד אחד היה לי 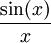 וזה שואף ל-1. בצד שני היה לי
וזה שואף ל-1. בצד שני היה לי 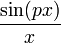 אז פשוט כפלתי וחילקתי ב-
אז פשוט כפלתי וחילקתי ב- 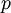 ואז בגלל ש-
ואז בגלל ש-  שואף ל-0, גם
שואף ל-0, גם 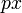 שואף ל-0 מה שאומר שגם
שואף ל-0 מה שאומר שגם 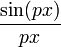 שואף ל-1.
שואף ל-1.
ואז כביכול היה יוצא 0 כי שני השברים מצמצמים אחד את השני.
הבעיה היא במה שאמרתי על 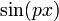 ו-
ו- 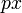 כי בדקתי במחשבון ושם זה נתן תוצאה אחרת.
כי בדקתי במחשבון ושם זה נתן תוצאה אחרת.
לכן רציתי לדעת איך לפתור את זה באמת.
תודה
תשובה
![\frac{\sin(px)}{px}\xrightarrow[x\to0]{}1](/images/math/8/6/c/86cd331396fee34faeb176f6cc3097bb.png) . קל לראות את זה לפי היינה. אם
. קל לראות את זה לפי היינה. אם 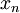 סדרה ששואפת ל-0 אזי גם
סדרה ששואפת ל-0 אזי גם 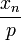 סדרה ששואפת ל-0, פשוט תציב בפונקציה ותקבל שבזכות ש-
סדרה ששואפת ל-0, פשוט תציב בפונקציה ותקבל שבזכות ש- 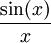 שואף ל-1, שגם הפונקציה הזו על הסדרה הנ"ל שואפת ל-1. (לא ניסחתי מדויק, אני אשאיר לך לתקן את הפערים).
שואף ל-1, שגם הפונקציה הזו על הסדרה הנ"ל שואפת ל-1. (לא ניסחתי מדויק, אני אשאיר לך לתקן את הפערים).
מצטער אבל לא ממש הבנתי איך התשובה שלך קשורה לשאלה שלי.
במחשבון יוצא שהפונ' שואפת ל-1.047 (וממש המספר הזה, לא 1)
אני אכתוב לך את מה שעשיתי ואני מקווה שתצליח להסביר לי מה היה לא נכון:
זה שווה ל:
ששווה ל:
ששווה ל:
וזה אמור להיות 0 זהותית (כלומר ממש 0, לא שואף ל-0...)
תשובה
דבר ראשון, אסור בתכלית האיסור, להחליף באמצע התרגיל את חלק מהגבולות למספר אליו הם שואפים. אחרת 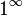 תמיד שווה 1 למרות שאנחנו יודעים שהוא יכול להיות e. ושוב, הייתי פותר את זה באמצעות כלל לופיטל, ולא בטוח איך אפשר אחרת.
תמיד שווה 1 למרות שאנחנו יודעים שהוא יכול להיות e. ושוב, הייתי פותר את זה באמצעות כלל לופיטל, ולא בטוח איך אפשר אחרת.
אוקי, אז נניח שהייתי מכניס את ה- 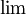 גם לשבר השני..
גם לשבר השני..
אני עדיין לא מבין למה זה לא היה עובד
(ותודה שאתה ממשיך לענות לי למרות החפירה..)
- מה הכוונה מכניס
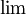 לשבר השני? אסור לך להחליף במספר, אתה נשאר עם אינסוף פחות אינסוף ולא מצליח לחשב. לא יהיה לך זהותית 0. אסור לך למחוק את
לשבר השני? אסור לך להחליף במספר, אתה נשאר עם אינסוף פחות אינסוף ולא מצליח לחשב. לא יהיה לך זהותית 0. אסור לך למחוק את 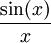
אז זה מה שאני לא מבין, למה אסור למחוק את 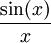 הרי זה אמור להיות 1 כש-
הרי זה אמור להיות 1 כש- 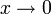
- כמו שאמרתי, לפי ההגיון הזה, גם
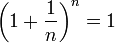 כי
כי 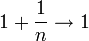 . במקרה זה, יש לך
. במקרה זה, יש לך 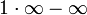 אסור להשתמש באריתמטיקה של גבולות במקרה זה. דוגמא נגדית פשוטה יותר:
אסור להשתמש באריתמטיקה של גבולות במקרה זה. דוגמא נגדית פשוטה יותר: 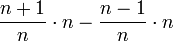 בשיטה שלך זה 0 זהותית. במציאות, זה שווה בדיוק 2.
בשיטה שלך זה 0 זהותית. במציאות, זה שווה בדיוק 2.
הבנתי. תודה רבה! (וסליחה על החפירה הארוכה, שוב)
שאלה
רציתי לבדוק אם אני צודק: דורשים למצוא נקודות אי-רציפות וסיווגן בפונקציות הבאות:
1) 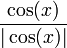
2) 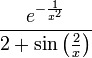
בשתיהן יצא לי 0 אי-רציפות סליקה. זה נכון?
תשובה
בראשון 0 אינה נקודת אי-רציפות בכלל... יש כמובן נקודות אי-רציפות אחרות, והן תמיד ממין ראשון. שים לב שהפונקציה הזו היא פשוט 1, 1- או לא מוגדרת.
בשני זה נכון, וזו אכן נקודת אי-הרציפות היחידה.
כן, בראשון התבלבלתי.. תודה רבה!
שאלה
אפשר בבקשה עזרה בתרגיל? צריך לבדוק האם 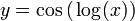 רבמ"ש בקטע הפתוח
רבמ"ש בקטע הפתוח 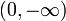 . אני לא ממש רואה את זה... (אין גבול בשאיפה ל-
. אני לא ממש רואה את זה... (אין גבול בשאיפה ל- 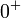 , אז ניסיתי להראות ע"י שתי סדרות שואפות ל-0 שאין רבמ"ש, לא ממש הולך לי...)
, אז ניסיתי להראות ע"י שתי סדרות שואפות ל-0 שאין רבמ"ש, לא ממש הולך לי...)
תשובה
מה לא הולך? 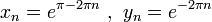 . שתי הסדרות שואפות ל-0, ולכן המרחק ביניהן שואף ל-0. אבל הפונקציה עליהן שווה 1 או 1-.
. שתי הסדרות שואפות ל-0, ולכן המרחק ביניהן שואף ל-0. אבל הפונקציה עליהן שווה 1 או 1-.
(זה לא כותב השאלה) אפשר פשוט לומר שהגבול באפס לא קיים, לכן הפונקציה לא רבמ"ש ב- 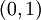 וכמובן שהיא לא רבמ"ש ב-
וכמובן שהיא לא רבמ"ש ב- 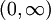 , לא?
, לא?
- (זה לא ארז) אני חושב שאסור, כי אז לפי מה שאתה אומר בגלל שלא קיים לsin x גבול באינסוף אז היא לא רבמ"ש...
- בכל מקרה, הדרך היחידה להוכיח שהגבול אינה קיים היא באמצעות הסדרות, כך שלא חסכת עבודה. באופן כללי, אפשר להוכיח שאם הגבול אינו קיים בצד הסופי, אזי הפונקציה לא רציפה שם במ"ש. זה נכון כי יש 2 אופציות: או שיש 2 סדרות ששואפות לצד הסופי (נגיד a) והפונקציה שואפת עליהן לגבולות שונים (וזה אוטומטית יוצר סתירה לרציפות במ"ש), או שיש סדרה ששואפת לאינסוף ואז הפונקציה אינה חסומה על קטע חסום, ולכן אינה רציפה במ"ש. אבל כמו שאמרתי, כך או כך זה דורש את בניית הסדרות.
- לאדע, לא עולה לי כל כך מהר הדוגמאות להפרכה. תודה בכל מקרה! יש לי עוד שאלה ממש קטנה, אני מנסה להוכיח שכשX שואף ל0, אז ln sin x / ln x שואף ל1.
- האם מותר לי להגיע לזה באמצעות המשפט של sin x / x =1 ? כי אז אני מכפיל בX, מפעיל LN על שני האגפים, מחלק בLN X ומקבל את הדרוש... תודה לעונה!
אסור. אין משפט שsinx/x=1 יש משפט שאומר שזה שואף לאחד... אבל לכפול בx זה כמו לכפול באפס וזה בוודאי אסור (אריתמטיקה של גבולות לא עוזרת פה). אפשר לפתור באמצעות כלל לופיטל, כמו שאמרתי אני לא יודע אם זה בחומר או לא.
זה לא בחומר, תודה בכל מקרה.!
שאלה
יש משהו שנורא מבלבל אותי.
נניח שיש לי את הפונקציה: 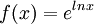
מצד אחד הנגזרת שלה היא 1, כי היא שווה ל-X
מצד שני, אם אני מתעלם מהעובדה שהדבר הזה הוא X ואני גוזר רגיל אני מקבל שהגזרת היא 1 חלקי X. מה עושים???
דרך אגב, ארז כתבתי לך בחזרה משהו בשאלה של ה- 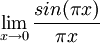 אז בבקשה תענה לי.
אז בבקשה תענה לי.
תשובה
לומדים לגזור!
![[e^{lnx}]' =e^{lnx} \cdot \frac{1}{x}=\frac{x}{x}=1](/images/math/0/3/4/034488632b6d8ac2e7d803ef9a0699bf.png)
חח אופס, סליחה.
שאלה - רבמ"ש
נכון, חפרנו על הנושא למרות שתהיה מקסימום שאלה אחת על זה במבחן, ובכל זאת:
נניח שאני רוצה להוכיח ש- f(x)=xsinx רבמ"ש. האם מותר לי לקחת x,y שמקיימים 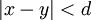 ולומר :
ולומר :
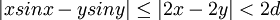 (מהסיבה שפונק' הסינוס חסומה ע"י 1 ו-1-) ?
(מהסיבה שפונק' הסינוס חסומה ע"י 1 ו-1-) ?
תשובה
בוודאי שלא. למשל 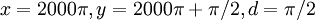 אז יוצא ש
אז יוצא ש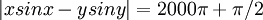
הטריק הוא בגדול לקחת 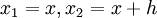 ולפתח לפי נוסחאות טריגונומטריות.
ולפתח לפי נוסחאות טריגונומטריות.
שאלה - טורים
ישבתי על זה הרבה ולא הצלחתי X:
- נתון שיש טור המוגדר ע"י סכום הסדרה an ובדומה סכום המוגדר ע"י סכום הסדרה bn
- ידוע שסיגמא AN זה A וסיגמא BN זה B
- מגדירים סדרה חדשה, CN שבמקומות האי זוגיים היא מקבלת את b1,b3,b5.... ובמקומות הזוגיים היא מקבלת את a1,a2,a3,...
- האם סיגמא CN מתכנס?
תשובה
לא של ארז: מקווה שזה נכון: סכום האי זוגיים של הסדרה b מתכנס לפי קריטריון ההשוואה, הסכום של a כמובן מתכנס לפני הנתון ולכן סכום טורים מתכנסים הוא מתכנס.
- מבחן ההשוואה נכון לטורים חיוביים בלבד. והתשובה היא בוודאי לא, אם לא נתון שהטורים חיוביים. לוקחים את הטור הקלאסי להתכנסות בתנאי
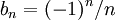 ולוקחים כל טור מתכנס אחר להיות a_n...
ולוקחים כל טור מתכנס אחר להיות a_n...
שאלה
שאלה מהמבחן של ראובן שנה שעברה שלא הצלחתי:
תהי an סדרה מתכנסת כך ש: 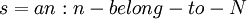 כאשר N זה המספרים הטבעיים. ואומרים ש-s היא קבוצה סופית.
צריך להוכיח שהחל מ-N מסויים, לכל n,m שגדולים ממנו, an=am.
כאשר N זה המספרים הטבעיים. ואומרים ש-s היא קבוצה סופית.
צריך להוכיח שהחל מ-N מסויים, לכל n,m שגדולים ממנו, an=am.
זה נראה לי נכון אבל אני לא יודע איך לכתוב את זה בצורה מתמטית.
תשובה
S הינה קבוצת כל האיברים בסדרה, והיא סופית. כלומר איבר בסדרה יכול להיות אחד מתוך מספר סופי של איברים (איבר מתוך S).
כעת, נגדיר את קבוצת ההפרשים 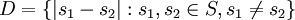 מכיוון שS סופית גם D סופית ולכן יש לה מינימום. נגדיר
מכיוון שS סופית גם D סופית ולכן יש לה מינימום. נגדיר 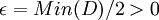 . כעת, לפי תנאי קושי, קיים
. כעת, לפי תנאי קושי, קיים 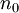 כך שלכל
כך שלכל 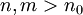 מתקיים
מתקיים 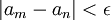 אבל אם
אבל אם 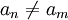 אזי
אזי 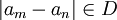 אבל
אבל
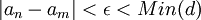 וזו סתירה.
וזו סתירה.
- סבבה תודה!
מבחן של ראובן
איפה יש את המבחן שלו משנה שעברה?
באתר של גיל
איפה זה, אפשר קישור?
תודה
שאלה
באחת משאלות האתגר שנתתם (זאת עם הגבולות החלקיים שכוללים את כל הממשיים), מותר לי פשוט להגיד ש-an היא הספירה של Q? אנחנו יודעים שאפשר לספור את Q אבל האם זה מספיק להסתמך על זה שקיימת ספירה כזאת ואז לרשום שנק' ההצטברות של Q הן כל R ולכן אלו הם הג"חים?
תשובה
השאלה היא האם משם אתה יכול להוכיח שכל מספר ממשי הוא גבול חלקי של הסדרה הנ"ל. אין משפט על הקשר שבין נקודת הצטברות של קבוצה, לבין הגבולות החלקיים של סדרה המכילה את איברי הקבוצה. האם הסדר לפי תבנה את הסדרה משנה?
- אוקיי.. יש לי סדרה אחרת שנראה לי שהיא תעבוד. את כל שאר תרגילי האתגר הצלחתי לפתור (חוץ מזה שדורש שימוש בקורס אחר שאין לי מושג מה לעשות שם חוץ מזה שאני בטוח כמעט לגמרי שזו הפרכה..)
- תשלח לי למייל בקצרה, אני אגיד לך אם צדקת. אגב, מתי המבחן שלכם?
- המבחן שלנו מחר :S
- הא, בהצלחה.. יכול להיות שאני אהיה מחר באוניברסיטה.. אבל זה כבר לא יעזור לאף אחד :)
שאלה
הוכח שאם f גזירה ב-(a,b), ונגזרתה חסומה בקטע, אזי f רבמ"ש שם. (WTF?!)
תשובה
נניח בשלילה שהיא אינה רציפה במ"ש, לכן קיים אפסילון, כך שלכל דלתא קיים זוג x,y כך שהמרחק בינהם קטן מדלתא, אבל המרחק בין f(x) לf(y) גדול מאפסילון. ולכן 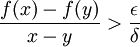 . ניקח
. ניקח 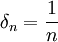 וניקח את הזוגות המתאימים
וניקח את הזוגות המתאימים 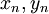 . אלה סדרות חסומות ולכן ניתן לקחת תת סדרה של
. אלה סדרות חסומות ולכן ניתן לקחת תת סדרה של 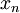 שמתכנסת, ואז תת-תת סדרה של y_n שמתכנסת וביחד נקבל שתי סדרות מתכנסות
שמתכנסת, ואז תת-תת סדרה של y_n שמתכנסת וביחד נקבל שתי סדרות מתכנסות 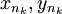 ומכיוון שהמרחק ביניהן הולך וקטן הן מתכנסות לאותו הגבול, נקרא לו L. אבל אז
ומכיוון שהמרחק ביניהן הולך וקטן הן מתכנסות לאותו הגבול, נקרא לו L. אבל אז
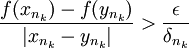 כלומר שואף לאינסוף, אבל זה חסום על ידי קבוע כפול הנגזרת (לפי תרגיל אחר שנתנו לכם) וזו סתירה.
כלומר שואף לאינסוף, אבל זה חסום על ידי קבוע כפול הנגזרת (לפי תרגיל אחר שנתנו לכם) וזו סתירה.
- אתה יכול בבקשה להסביר למה הכוונה ב"זוגות המתאימים Xn Yn" - הכוונה היא לאותן סדרות שעזרו לך להוכיח או להפריך משהו בהרבה תרגילים אחרים בעמוד זה?
- ועוד משהו, למה הכוונה חסום ע"י קבוע כפול הנגזרת?
"... כך שלכל דלתא קיים זוג x,y..." הזוג הזה.
חסום ע"י הכוונה "קטן מ.."
שאלה
נניח שאנחנו מקבלים פונקצייה כמו:
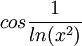 . האם מצפים מאתנו להתייחס אליה כמוגדרת גם ב-x<0 (כפי שהיא כתובה), או ללכת צעד אחד קדימה ולהפוך את זה ל:
. האם מצפים מאתנו להתייחס אליה כמוגדרת גם ב-x<0 (כפי שהיא כתובה), או ללכת צעד אחד קדימה ולהפוך את זה ל: 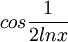 ?
?
שאלה נוספת - כדי להוכיח שלא קיים גבול בנק' x=1, במקרה זה, האם מותר לי להשתמש בנימוק המילולי הבא (?): הפונקצייה מבצעת אינסוף מחזורים בכל סביבה של x=1, לכן הגבול לא קיים. אם לא, איך אחרת אפשר לנמק את אי-קיום הגבול בנק', בלי פשוט לומר שהפונק' שבתוך ה-cos שואפת לאינסוף?
תשובה
כמובן שהיא מוגדרת באפס. לא עושים שום צעדים קדימה או אחורה. זה כמו שx/x אינה מוגדרת באפס.
לא, תקרא את הדוגמאות האחרות (כמעט זהות) בנושא. בונים 2 סדרות ששואפות ל1 אבל הפונקציה עליהן הולכת לפלוס אחד או מינוס אחד ולכן אין גבול לפי היינה.
שאלה
האם זהו משפט נכון? M = SUP A אם"ם לכל e>0 קיים a ששייך לA כך ש M-e<a
תשובה
לא מדוייק
M=supA אם"ם M חסם עליון וגם e>0 קיים a ששייך לA כך ש M-e<a
M חסם עליון אומר M גדול מכל האיברים בקבוצה, והתנאי עם האפסילון נותן את המינימליות של M. אם הוא לא היה מתקיים, אז M-e היה חסם עליון קטן יותר.
שאלה
האם הפו' 1 חלקי n רציפה בקטע [0,1) ? ורבמ"ש?
תשובה
רציפה שם, ברור, זה פונקציה רציפה חלקי רציפה, כאשר הפונקצה במכנה שונה מאפס.
היא אינה רציפה שם במ"ש כי היא אינה חסומה שם. ופונקציה שרציפה במ"ש על קטע סגור חסומה בו.
- אבל זה לא קטע סגור, הוא חצי פתוח O:
- שגיאה שלי, הכוונה הייתה לקטע חסום ולא סגור. פונקציה רציפה במ"ש על קטע חסום חסומה בו.
- זאת אומרת שהפעם היחידה שאנחנו צריכים ממש להפריך את הרבמ"ש שלא ע"י משפט, זה כשהיא רציפה והגבול באינסוף או מינוס אינסוף אינו קיים?
- לא. לפני שנייה הייתה דוגמא של coslogx
- זאת אומרת שהפעם היחידה שאנחנו צריכים ממש להפריך את הרבמ"ש שלא ע"י משפט, זה כשהיא רציפה והגבול באינסוף או מינוס אינסוף אינו קיים?
- שגיאה שלי, הכוונה הייתה לקטע חסום ולא סגור. פונקציה רציפה במ"ש על קטע חסום חסומה בו.
תודה רבה :)
הוכחת משפט ערך הביניים
במייזלר יש הוכחה שמשתמשת בטענת עזר שקשורה בחיתוך עם ציר ה-x של הפונקצייה. למה לא לפשט את זה להוכחה כזו (האם היא תקינה?):
תהי f רציפה ב-[a,b], אזי אם 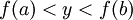 נבנה סדרת קטעים
נבנה סדרת קטעים ![I_n=[a_n,b_n]](/images/math/8/9/6/896f17899a5f55ed35de918753570d00.png) כך ש-
כך ש- 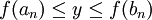 , כאשר
, כאשר ![I_1=[a,b], I_n=[a_n,b_n]](/images/math/c/d/5/cd5f7de6db594058973b76aa3319e12b.png) , ו-
, ו-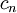 מוגדרת:
מוגדרת: 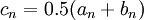 , כך שאם
, כך שאם 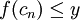 נגדיר
נגדיר ![I_{n+1}=[c_n,b_n]](/images/math/9/3/0/930348e8dc0d854db40dd69b830ac016.png) , ואחרת
, ואחרת ![I_{n+1}=[a_n,c_n]](/images/math/3/9/a/39a8386c84fdd351007db14f80851949.png) . לפי קנטור קיימת נק' יחידה
. לפי קנטור קיימת נק' יחידה  באמצע כך ש-
באמצע כך ש- 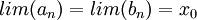 , ובגלל הרציפות של f נקבל ש-
, ובגלל הרציפות של f נקבל ש- 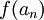 ו-
ו- 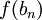 שואפים להיות y.
שואפים להיות y.
תשובה
זו הוכחה נכונה, אמנם חסרת כמה פרטים, אבל נכונה.
שאלה
ארז באחת השאלות למעלה אמרת: "אפשר להוכיח שאם הגבול אינו קיים בצד הסופי, אזי הפונקציה לא רציפה שם במ"ש."
אבל כפי שמישהו מעלייך אמר, אז sin רציפה במידה שווה בכל R ואין לה גבול באין-סוף
- באיזה מובן אינסוף הינו "צד סופי"??
- אופס, הלחץ מהמבחן עושה את שלו..
- אם כבר הגענו לנושא הזה:
- א) אין אריתמטיקה בין פונקציות רבמ"ש נכון?, לדוגמא כפל פונ' שהן רבמ"ש (נגיד בקטע [a,b]) לא יהיה בהכרח רבמ"ש נכון?
- ב) איך מוכיחים ש-sin רבמ"ש ע"פ הגדרה (בלשון דלתא ואפסילון)? (מה הטריק השם, איזה איקסים לוקחים?)
תשובה
א. יש חצי אריתמטיקה. כפל אין (x כפול x) אבל חיבור יש כמובן. בנוסף יש הרכבה, הרכבה של רציפות במ"ש הינה רציפה במ"ש
ב. תרגיל כללי הוא להוכיח שכל פונקציה שרציפה על כל הממשיים ומחזורית הינה רציפה במ"ש. סינוס זה מקרה פרטי של המשפט הגדול הזה. בצורה דומה 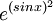 הינה רציפה במ"ש למשל..
הינה רציפה במ"ש למשל..
- ב-ב' זה בגלל ש-sin רציפה בקטע סגור, ואז היא רבמ"ש בו, ובעצם בגלל שהיא מחזורית אז זה מעיין איחוד אין סופי של אותו הקטע נכון?
ובדוגמא שנתת - איך מוכיחים שהפונ' הזאת מחזורית?
- לכל פונקציה מחזורית זה נכון. צ"ל להוכיח את זה במדויק, אבל מה שציינת זו אכן הדרך.
- פשוט מציבים
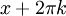 ורואים מיידים שזה שווה לערך של x לכל x
ורואים מיידים שזה שווה לערך של x לכל x
- אוקי, תודה :)
שאלה
שני דברים: א) צריך להוכיח במבחן שפונקציה רציפה ומחזורית היא רבמ"ש בכל פעם שמסתמכים על זה? אפשר לתת כאן הוכחה ליתר ביטחון? ב) ארז, אתה יכול להעלות פתרונות לשאלות אתגר? מחר (חמישי) המבחן ומעניין אותי לדעת איך לפתור את השאלה שקשורה לקורסים אחרים...
תשובה
אני לא יודע על מה מותר או אסור לכם להסתמך. אבל ההוכחה הולכת ככה: אתה מחלק את כל הממשיים לקטעים באורך המחזוריות, על כל קטע סגור וחסום הפונקציה רציפה במ"ש. עכשיו, כל שתי נקודות מספיק קרובות יכולות להיות במצב אחד מבין שניים: או ששתיהן באותו קטע, או שהן בקטעים חופפים. לכן נחלק גם את הממשיים לקטעים באורך פעמיים המחזוריות, וגם שם הפונקציה רציפה במ"ש. ולכן ניקח את הדלתא המינימלי בין זה של פעמים הקטע וזה של הקטע, וכל שתי נקודות שקרובות עד כדי הדלתא הזה, יהיה קרובות עד כדי האפסילון.
אני אשתדל להעלות פתרונות, לא בטוח שאני אספיק מלאים, אבל לפחות אני אתן את העיקר
שאלה
ארז איך מוכיחים ש 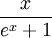 רבמ"ש?
רבמ"ש?
- היא לא רבמ"ש, אמנם כשהיא שואפת לאינסוף יש לה גבול והוא 0, אבל כשתשאיף אותה למינוס אינסוף היא תשאף למינוס אינסוף.
- המשפט בבדיקת אינסוף ומינוס אינסוף הוא לא אם"ם, אלא רק כיוון אחד. היא אפילו כן רבמ"ש, כי היא רבמ"ש בצד החיובי של ציר הx, ובצד השלילי הוא מתנהג כמו x שהוא לינארי ולכן רבמ"ש. (לא הוכחה פורמלית)
- אפשר בבקשה הוכחה פורמלית
- צודק ברעיון של הבדיקה של האינסוף, אבל לא הבנתי למה אתה אומר שבצד השלילי הוא מתנהג כמו x לינארי - הוא הרי שואף למינוס אינסוף בצורה קיצונית, יותר מהר מכל פונקצייה אחרת (אם לא הייתי יודע שזה מוגדר הייתי בטוח שזו אסימפטוטה).
- לא, כי במינוס אינסוף המכנה שואף ל1 והמונה הוא x. כלומר ככל שהוא מתקרב למינוס אינסוף, הוא מתקרב (שואף) לx.
- בנוסף, ההוכחה הפורמלית רק אפשרית ישירות מההגדרה עם אפסילון ודלטא.
- רגע, אז אפשר לחלק את זה לשני קטעים אפס עד איןסוף ומינוס אינסוף עד אפס ולהגיד שבראשון היא רציפה במ"ש בגלל גבולות בקצוות, ובשני היא מתנהגת כמו הגרף של X, ואז רק נותר להראות מה קורה אם לוקחים X1 מקטע אחד ו-X2 מהקטע השני?
- בעקרון כן, אבל זה לא כל כך פורמלי. הכל מסתמך על זה שאם פונקציה רבמ"ש בשתי קטעים אז היא רבמ"ש באיחוד שלהם. זה נראה נכון הגיונית, אבל אני לא בטוח שמותר להשתמש בזה במבחן.
- אבל בגלל זה אמרתי שרק צריך לבדוק מה קורה אם X1 מהקע הראשון וX2 מהקטע השני -זאת הבדיקה של האיחוד. אבל האם יש "מבחן השוואה" לרציפות במ"ש? כי אם לא אז איך אני יכול להגיד שמתחת ל-0 הפונ' מתנהגת כמו X? הרי היא מתנהגת בין X/2 ל-X (אמנם שתיהן רציפות, אבל בגלל זה שאלתי על מבחן ההשוואה)...
- בעקרון כן, אבל זה לא כל כך פורמלי. הכל מסתמך על זה שאם פונקציה רבמ"ש בשתי קטעים אז היא רבמ"ש באיחוד שלהם. זה נראה נכון הגיונית, אבל אני לא בטוח שמותר להשתמש בזה במבחן.
- רגע, אז אפשר לחלק את זה לשני קטעים אפס עד איןסוף ומינוס אינסוף עד אפס ולהגיד שבראשון היא רציפה במ"ש בגלל גבולות בקצוות, ובשני היא מתנהגת כמו הגרף של X, ואז רק נותר להראות מה קורה אם לוקחים X1 מקטע אחד ו-X2 מהקטע השני?
- צודק ברעיון של הבדיקה של האינסוף, אבל לא הבנתי למה אתה אומר שבצד השלילי הוא מתנהג כמו x לינארי - הוא הרי שואף למינוס אינסוף בצורה קיצונית, יותר מהר מכל פונקצייה אחרת (אם לא הייתי יודע שזה מוגדר הייתי בטוח שזו אסימפטוטה).
- אפשר בבקשה הוכחה פורמלית
- המשפט בבדיקת אינסוף ומינוס אינסוף הוא לא אם"ם, אלא רק כיוון אחד. היא אפילו כן רבמ"ש, כי היא רבמ"ש בצד החיובי של ציר הx, ובצד השלילי הוא מתנהג כמו x שהוא לינארי ולכן רבמ"ש. (לא הוכחה פורמלית)
- (מישהו אחר) ארז קראתי את מה שנכתב פה, אתה יכול להגיד בקצרה מהי הדרך לומר שזה אכן רבמ"ש (או להפריך את זה..)?
- אני לא ארז, אבל שוב: אפשר להוכיח ישירות לפי הגדרה עם אפסילון ודלטא.
- (מישהו אחר) ארז קראתי את מה שנכתב פה, אתה יכול להגיד בקצרה מהי הדרך לומר שזה אכן רבמ"ש (או להפריך את זה..)?
- אני שוב לא בטוח איך הכוונה לפתור את השאלה, כי יש דרכים בעזרת נגזרות (כמו ששאלו באתר, אם הנגזרת חסומה הפונקציה רציפה במ"ש) אבל לא למדנו את המשפטים האלה, לכן אני לא יודע מאיפה השאלה ובאיזה שיטה צריך לפתור...
תודה!
ארז, אמרנו את זה כבר בלינארית, אבל אתה ממש בן אדם מדהים! לא הייתי מצפה מהמתרגל הכי טוב שיעזור לקבוצה בקורס שהוא לא מלמד, ובטח ובטח לא בכל כך מסירות! תודה רבה על כל העזרה והתמיכה (והאתגרים :P) והלימוד המצויין! בבקשה תתרגל אותנו אינפי 2! אין לי (ולכולנו) מילים להודות לך!
איך להגיד את זה שיינר, אם היית וקטור, לא היה אפשר לנרמל אותך כי אתה פשוט לא נורמלי! אם היית פונקציה, היית שואף לאינסוף בכל סביבה של כל נקודה אם היית קטע, היית כל הישר.
אם היית מצחיק אחי אולי ההיתי צוחק
- ואם לא היה לך כזה קטן אולי לא היית צריך לרדת על אחרים בשביל לצאת גבר, אחי ;)
בוא בוא תסביר את עצמך כי וואלה לא הבנתי ..
- עזוב, עזוב, אי הבנה, זה הכל
- ארז כל הכבוד! אבסורד שאתה המתרגל שהכי עזר לנו בקורס הזה
- אני גם מעדיף שתתרגל אותנו באינפי 2
- בסופו של דבר הוא כן מתרגל (של קבוצה א') :)
הכרזה
יש ציונים!!!
שאלה ברציפות במידה שווה
שלום, רציתי הוכחה בבקשה לתרגיל ברציפות במידה שווה.
האם איקס כפול סינוס איקס, רציפה במ"ש בקטע בין מינוס אינסוף לאינסוף..
תודה רבה!!
תשובה
קח 2 סדרות
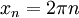 ו
ו 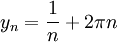 . ברור שההפרש בינהן שואף לאפס, אבל
. ברור שההפרש בינהן שואף לאפס, אבל 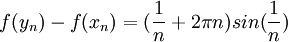 אבל הביטוי הזה שואף ל
אבל הביטוי הזה שואף ל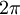 ולכן בוודאי גדול מקבוע שגדול מאפס (למשל אחד) החל משלב מסויים...
ולכן בוודאי גדול מקבוע שגדול מאפס (למשל אחד) החל משלב מסויים...
- תודה רבה ארז! אתה תותח!
שאלה בקשר למשפט על רציפות במידה שווה
קראתי כאן וגם בהרצאה משפט שמדבר על: פונקציה שרציפה בקטע (a,b) (כאשר a ,b או שניהם הם אינסוף או מינוס אינסוף), אז אם הגבולות בהם קיימים וסופיים, הפונקציה רציפה במידה שווה. אם יש לי קטע פתוח בין 0 לאינסוף, ופונקציה של (סינוס של איקס) חלקי איקס בריבוע, ראיתי שהוא בודק את הגבולות באינסוף וב0 מימין, אבל בדוגמא אחרת, של סינוס של אחד חלקי איקס, בין אחד לאינסוף, הוא בדק רק את הגבול כשאיקס שואף לאינסוף. למה הוא לא בדק את הגבול כשאיקס שואף לאחד מימין? כי הפונקציה מוגדרת באחד ולכן לא צריך לבדוק את זה? (ולעומת זאת בדוגמא הראשונה, כשאיקס שווה לאפס אז זה תחום ההגדרה ולכן צריך כן לבדוק?). ושאלה אחרונה בקשר למשפט שאמרתי, בהרצאה הוא לא ציין שa או b חייבים להיות אינסוף, האם זה נכון גם כשהם מספרים ממשיים? תודה רבה!!
תשובה
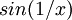 רציפה באחד ולכן ברור שהגבול שם קיים ואין צורך בבדיקה נוספת. כאשר היא לא רציפה (מסיבה של תחום הגדרה או כל סיבה אחרת, אז יש לבדוק מה הגבול.
רציפה באחד ולכן ברור שהגבול שם קיים ואין צורך בבדיקה נוספת. כאשר היא לא רציפה (מסיבה של תחום הגדרה או כל סיבה אחרת, אז יש לבדוק מה הגבול.
כן, כי אם f רציפה בקטע הפתוח (a,b) ויש לה גבולות חד צדדים בקצות הקטע, אזי לפי הגדרה f רציפה בקטע הסגור [a,b]. ואז לפי משפט f רציפה בו במ"ש.
- הבנתי לגמרי עכשיו, תודה ענקית!! :]
שאלה בנושא רציפות במידה שווה
רציתי לדעת בבקשה איך מוכיחים שהפונקציה קוסינוס של שורש של ערך מוחלט של X רציפה במידה שווה בR. אולי להפריד ל2 מקרים כשX>0 וכשX<0.. תודה רבה!!!!
תשובה
כן להפריד למקרים, ואז זו הרכבה של רציפות במ"ש. את שורש איקס אפשר להוכיח לפי ההגדרה באמצעת כפל בצמוד.
- הבנתי, תודה שוב ושיהיה לך לילה טוב..
משפט הערך הממוצע
שלום, רציתי לדעת בבקשה אם נלמד משפט הערך הממוצע בכיתה..? תודה רבה :]
תשובה
בהתחשב בעובדה שאינפי 2 כבר התחיל ובמסגרתו למדנו המשפט הזה, השאלה הזו קצת מפתיעה.
משפט הערך הממוצע הינו משפט לגרנז' ולמדנו אותו בתחילת סימסטר ב' (ולא כחלק מסמיסטר א'...)
- לא הסברתי טוב, אני יודע שהוא נלמד, השאלה אם הוא יכול להיות במבחן מועד ב' באינפי 1 אבל הבנתי שלא.. תודה על התשובה..
תרגיל ברציפות במידה שווה
שלום ארז, יש לי תרגיל שלא הצלחתי לפתור ואני ישמח אם תעזור לי לבדוק רציפות במידה שווה של (x*cos(1/x^2 בקטע שבין (אינסוף, 0). לעניות דעתי צריך להפריך. ועוד שאלה קטנה בקשר להפרכה: צריך לקחת שתי סדרות כך שאחד התנאים הוא שהחיסור ביניהן כשמשאיפים לאינסוף ישאף ל-0. אם הוא שווה ל-0 ולא שואף ל-0, האם התנאי הזה התקיים? (כמובן שצריך לבדוק מה קורה כשמציבים את הסדרות בפונקציה אך אני מדבר רק על התנאי הראשון). אודה לך על תשובתך!
תשובה
אם החיסור בינהן שווה אפס אז זה אותה סדרה, ואז בוודאי שהתנאי על כך שההפרש בין הפונקציות מופעלות על הסדרות צריך להיות גדול מקבוע, לא יתקיים.
ודווקא נראה לי שצריך להוכיח, כי הנגזרת חסומה. אני אנסה לפתור את זה מחר. = תודה מקרב לב
2 הגדרות ו2 שאלות ברבמ"ש
היי ארז מה נשמע? יש לי בבקשה כמה שאלות..
1) בהגדרת היינה בורל במבחן, מספיק לרשום: "S קומפקטית אם ורק אם היא חסומה וסגורה", זה מספיק או שצריך להסביר גם מה זה קומפקטית..?
2) אם יש שאלה לנסח את משפט בולצ'אנו ויירשטראס, איזה מהם? עבור סדרות, קבוצות או פונקציות? או מה שאני בוחר?
3) רבמ"ש: איקס כפול קוסינוס של איקס בין מינוס אינסוף לאינסוף.. (בטח להפריך)
4) רבמ"ש: איקס כפול לוג של איקס בין אפס לאינסוף (לפי דעתי צריך להפריך כי מבחינת אינטואיציה, לוג איקס שואף ממינוס אינסוף ואם נכפיל באיקס אז זה עוד יותר מינוס אינסוף..)
אלה השאלות האחרונות שאני אשאל.. מקווה שיהיה לך זמן.. תודה רבה רבה רבה, אם נצליח זה רק בזכותך תאמין לי.. ואם להגיד את האמת אז חבל שלא הבנתי את זה בתחילת סמסטר א', העיקר שעכשיו אני מבין.. תודה שוב :]
תשובה
1,2 אלה שאלות למרצה.
3. זה בדיוק כמו xsinx שעניתי עליו
4. זה להפריך, אפשר עם שתי הסדרות 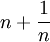 ו
ו  . צריך לשחק קצת עם הlog ובעיקר לשים לב שזו הפונקציה
. צריך לשחק קצת עם הlog ובעיקר לשים לב שזו הפונקציה 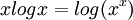 וההפרש בין שני לוגים הוא לוג של החלוקה.
וההפרש בין שני לוגים הוא לוג של החלוקה.
- * תודה רבה!! אני אנסה את מה שאמרת.. שיהיה בהצלחה לכל מי שניגש.. וארז, תודה על הכל!!
שאלה
במועד ב' באינפי 1, ניתן להשתמש בכלל לופיטל?
לא בטוח באיזה קורס, אבל אם לא למדתם את זה באינפי 1 לא ניתן להשתמש בזה במבחן
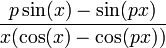
![\lim\limits_{x\to0}\left[\frac{\pi\sin(x)-\sin(\pi x)}{x(\cos(x)-\cos(\pi x))}\right]](/images/math/c/e/c/cec1773dd7a78cfc7680f54fbd6f3477.png)
![\lim_{x\to0}\left[\frac{\pi\sin(x)}{x(\cos(x)-\cos(\pi x))}-\frac{\sin(\pi x)}{x(\cos(x)-\cos(\pi x))}\right]](/images/math/b/c/0/bc0a68a9139593509ffc4938e751ae81.png)
![\lim_{x\to0}\left[\frac{\pi}{\cos(x)-\cos(\pi x)}-\frac{\pi\sin(\pi x)}{\pi x(\cos(x)-\cos(\pi x))}\right]](/images/math/d/1/1/d113ca4a619ef11cb4608c6ce7bc7fe1.png)
![\lim_{x\to0}\left[\frac{\pi}{\cos(x)-\cos(\pi x)}-\frac{\pi}{(\cos(x)-\cos(\pi x))}\right]=0](/images/math/f/7/6/f765b3743a3188f538eefb87555d89e0.png)