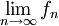
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
ארכיון
ארכיון 1 - תרגיל 1 ו2
ארכיון 2 - תרגיל 3
ארכיון 3 - תרגיל 3
ארכיון 4 - תרגיל 4
ארכיון 5 - תרגיל 4,5
ארכיון 6 - תרגיל 6
ארכיון 7 - (מי עוקב)
ארכיון 9 - לקראת הבוחן
ארכיון 10 - פוסט בוחן
ארכיון 11 - תרגיל 9
ארכיון 12 - תרגיל 9
ארכיון 13 - תרגיל 10
ארכיון 14 - תרגיל 10
ארכיון 15 - תרגיל 10
שאלה
בבוחן, בשאלה 1, היה אפשר גם להוכיח את האי השיוויון הימני עם טיילור עבור x0=0,n=2 לא?
- לא נראה לי... מאיפה אנחנו יודעים איך השארית משפיעה?
שאלה
אם אני רוצה לחשב את סכום הטור : 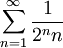 , אבל כשאני מפרק אותו לאינטגרל לפי רימן (חלוקה של
, אבל כשאני מפרק אותו לאינטגרל לפי רימן (חלוקה של  ) אז אני מקבל שזה שווה לאינטגרל:
) אז אני מקבל שזה שווה לאינטגרל: 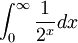 וזה יוצא
וזה יוצא 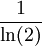 , למרות שהסכום לפי מה שבדקתי אמור לצאת
, למרות שהסכום לפי מה שבדקתי אמור לצאת 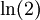 . איפה הטעות שלי? אני מניח שהיא איפה שהמרתי סכום לאינטגרל לא אמיתי... איך אפשר לחשב את זה בכל מקרה?
. איפה הטעות שלי? אני מניח שהיא איפה שהמרתי סכום לאינטגרל לא אמיתי... איך אפשר לחשב את זה בכל מקרה?
תשובה
קודם כל אין פה כלל חלוקת רימן (שכן המרחק בין נקודות הדגימה הוא אספוננציאלי עולה, ואילו האורכים הולכים ויורדים לאפס). אפילו אם הייתה, זו חלוקה אינסופית אחת ולא גבול של חלוקות.
פותרים את זה בדיוק כפי שפתרנו אתמול בכיתה. נגדיר 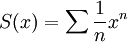 קל לראות שרדיוס ההתכנסות הוא אחד ולכן זה טור חזקות שמתכנס במ"ש בסביבה של חצי. ברור שסכום הטור שמעניין אותנו הוא
קל לראות שרדיוס ההתכנסות הוא אחד ולכן זה טור חזקות שמתכנס במ"ש בסביבה של חצי. ברור שסכום הטור שמעניין אותנו הוא 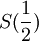 . מכיוון שההתכנסות היא במ"ש מותר לגזור איבר איבר ולקבל
. מכיוון שההתכנסות היא במ"ש מותר לגזור איבר איבר ולקבל 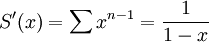 .
.
לכן 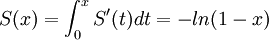 ולכן
ולכן 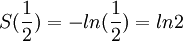
עד כדי טעות...
הערה: זה תרגיל נחמד שנותן לנו נוסחא לחישוב lnx עם דיוק אספוננטציאלי עבור x>1 (עבור x>1 ניקח את). הנוסחא
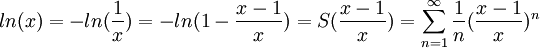
נחמד מאוד, הבנתי! על הטריק עם ה-ln שכתבת בהערה אני לא חושב שהייתי מצליח לעלות, אבל אני אזכור אותו עכשיו, תודה רבה!!
שאלה
יהי 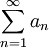 טור חיובי מתכנס, ו-
טור חיובי מתכנס, ו- 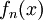 סדרת פונקציות, כך שלכל n טבעי מתקיים:
סדרת פונקציות, כך שלכל n טבעי מתקיים: 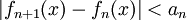 . הוכח או הפרך :
. הוכח או הפרך :  מתכנסת במידה שווה.
מתכנסת במידה שווה.
אני מתקשה להבין את הבעייה של ההתכנסות במ"ש במקרה הזה... אז אחרי שלא הצלחתי להפריך, ניסיתי להוכיח, וראיתי שזה קרוב יותר לקריטריון של קושי להתכנסות במ"ש, אז מספיק להראות שאם לכל k יש n טבעי שעבורו 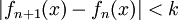 , אז גם נובע שלכל m>n מתקיים התנאי של קושי, אבל זה בדיוק מה שאני לא מצליח להראות... איך אני יכול להפריך ע"י מציאת סדרת פונקציות שהפרש של כל פונקציות קרובות שואף לאפס, אבל כשה-n גדל הפונקציות החדשות שנוצרות רחוקות יותר עד כדי חוסר התכנסות במידה שווה או אפילו חוסר התכנסות?
, אז גם נובע שלכל m>n מתקיים התנאי של קושי, אבל זה בדיוק מה שאני לא מצליח להראות... איך אני יכול להפריך ע"י מציאת סדרת פונקציות שהפרש של כל פונקציות קרובות שואף לאפס, אבל כשה-n גדל הפונקציות החדשות שנוצרות רחוקות יותר עד כדי חוסר התכנסות במידה שווה או אפילו חוסר התכנסות?
תשובה
זה תרגיל מאינפי 1 בתכלס.
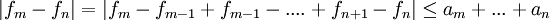
אבל לפי תנאי קושי להתכנסות טורים הצד הימני קטן מאפסילון.
- אהההה, הבנתי, וזה מתקיים עבור n,m גדולים מספיק (כלומר שגדולים מ-n0 התחלתי)... יפה! הייתי צריך לנסות לקשר את זה לסכום הטור... תודה רבה :) !!!
שאלה
אני מוכרח להבין, מה בעצם המשמעות של "התכנסות במידה שווה" של סדרת פונקציות? ז"א, מה המשמעות הגרפית של זה, בלי שימוש באפסילון וכ'ו? מה בעצם ה"מידה שווה" כאן?
תשובה
המשמעות היא שבכל נקודה בפונקציה ההתכנסות היא באותה מהירות פחות או יותר. גרפית, אתה מעתיק את פונקצית הגבול אפסילון למעלה ואפסילון למטה, ואז החלק מn_0 מסויים כל הפונקציות בסדרה מצויירות בגרף בין שתי ההזזות של פונקצית הגבול.
במילים אחרות, הפונקציות נמצאות במרחק 'קבוע' מפונקצית הגבול ללא תלות באיקס. למה זה עוזר? למשל רציפות. תהי סדרת פונקציות רציפות. ניקח פונקציה f_n מהסדרה עבור n מספיק גדול, ונקח סביבה קטנה של x_0 כלשהו. מתוך רציפות, f_n שולחת את סביבה של x_0 קרוב מאד לf(x_0). אבל, כל f_n שולחת כל נקודה בסביבה קרוב מאד לפונקצית הגבול באותה נקודה והמרחק לא תלוי בבחירת הנקודה. לכן גם כל הסביבה של פונקצית הגבול קרובה מאד לf(x_0( ויוצא שגם פונקצית הגבול רציפה.