שאלה
בבוחן, בשאלה 1, היה אפשר גם להוכיח את האי השיוויון הימני עם טיילור עבור x0=0,n=2 לא?
- לא נראה לי... מאיפה אנחנו יודעים איך השארית משפיעה?
שאלה
אם אני רוצה לחשב את סכום הטור : 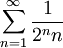 , אבל כשאני מפרק אותו לאינטגרל לפי רימן (חלוקה של
, אבל כשאני מפרק אותו לאינטגרל לפי רימן (חלוקה של  ) אז אני מקבל שזה שווה לאינטגרל:
) אז אני מקבל שזה שווה לאינטגרל: 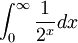 וזה יוצא
וזה יוצא 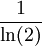 , למרות שהסכום לפי מה שבדקתי אמור לצאת
, למרות שהסכום לפי מה שבדקתי אמור לצאת 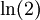 . איפה הטעות שלי? אני מניח שהיא איפה שהמרתי סכום לאינטגרל לא אמיתי... איך אפשר לחשב את זה בכל מקרה?
. איפה הטעות שלי? אני מניח שהיא איפה שהמרתי סכום לאינטגרל לא אמיתי... איך אפשר לחשב את זה בכל מקרה?
תשובה
קודם כל אין פה כלל חלוקת רימן (שכן המרחק בין נקודות הדגימה הוא אספוננציאלי עולה, ואילו האורכים הולכים ויורדים לאפס). אפילו אם הייתה, זו חלוקה אינסופית אחת ולא גבול של חלוקות.
פותרים את זה בדיוק כפי שפתרנו אתמול בכיתה. נגדיר 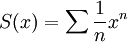 קל לראות שרדיוס ההתכנסות הוא אחד ולכן זה טור חזקות שמתכנס במ"ש בסביבה של חצי. ברור שסכום הטור שמעניין אותנו הוא
קל לראות שרדיוס ההתכנסות הוא אחד ולכן זה טור חזקות שמתכנס במ"ש בסביבה של חצי. ברור שסכום הטור שמעניין אותנו הוא 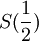 . מכיוון שההתכנסות היא במ"ש מותר לגזור איבר איבר ולקבל
. מכיוון שההתכנסות היא במ"ש מותר לגזור איבר איבר ולקבל 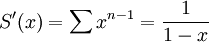 .
.
לכן 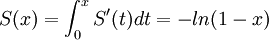
ולכן 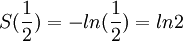
עד כדי טעות...
הערה: זה תרגיל נחמד שנותן לנו נוסחא לחישוב lnx עם דיוק אספוננטציאלי עבור x>1 (עבור x<1 ניקח את). הנוסחא
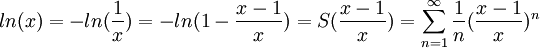
נחמד מאוד, הבנתי! על הטריק עם ה-ln שכתבת בהערה אני לא חושב שהייתי מצליח לעלות, אבל אני אזכור אותו עכשיו, תודה רבה!!
שאלה
יהי 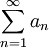 טור חיובי מתכנס, ו-
טור חיובי מתכנס, ו- 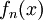 סדרת פונקציות, כך שלכל n טבעי מתקיים:
סדרת פונקציות, כך שלכל n טבעי מתקיים: 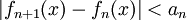 . הוכח או הפרך :
. הוכח או הפרך :  מתכנסת במידה שווה.
מתכנסת במידה שווה.
אני מתקשה להבין את הבעייה של ההתכנסות במ"ש במקרה הזה... אז אחרי שלא הצלחתי להפריך, ניסיתי להוכיח, וראיתי שזה קרוב יותר לקריטריון של קושי להתכנסות במ"ש, אז מספיק להראות שאם לכל k יש n טבעי שעבורו 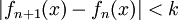 , אז גם נובע שלכל m>n מתקיים התנאי של קושי, אבל זה בדיוק מה שאני לא מצליח להראות... איך אני יכול להפריך ע"י מציאת סדרת פונקציות שהפרש של כל פונקציות קרובות שואף לאפס, אבל כשה-n גדל הפונקציות החדשות שנוצרות רחוקות יותר עד כדי חוסר התכנסות במידה שווה או אפילו חוסר התכנסות?
, אז גם נובע שלכל m>n מתקיים התנאי של קושי, אבל זה בדיוק מה שאני לא מצליח להראות... איך אני יכול להפריך ע"י מציאת סדרת פונקציות שהפרש של כל פונקציות קרובות שואף לאפס, אבל כשה-n גדל הפונקציות החדשות שנוצרות רחוקות יותר עד כדי חוסר התכנסות במידה שווה או אפילו חוסר התכנסות?
תשובה
זה תרגיל מאינפי 1 בתכלס.
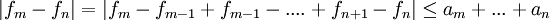
אבל לפי תנאי קושי להתכנסות טורים הצד הימני קטן מאפסילון.
- אהההה, הבנתי, וזה מתקיים עבור n,m גדולים מספיק (כלומר שגדולים מ-n0 התחלתי)... יפה! הייתי צריך לנסות לקשר את זה לסכום הטור... תודה רבה :) !!!
שאלה
אני מוכרח להבין, מה בעצם המשמעות של "התכנסות במידה שווה" של סדרת פונקציות? ז"א, מה המשמעות הגרפית של זה, בלי שימוש באפסילון וכ'ו? מה בעצם ה"מידה שווה" כאן?
תשובה
המשמעות היא שבכל נקודה בפונקציה ההתכנסות היא באותה מהירות פחות או יותר. גרפית, אתה מעתיק את פונקצית הגבול אפסילון למעלה ואפסילון למטה, ואז החלק מn_0 מסויים כל הפונקציות בסדרה מצויירות בגרף בין שתי ההזזות של פונקצית הגבול.
במילים אחרות, הפונקציות נמצאות במרחק 'קבוע' מפונקצית הגבול ללא תלות באיקס. למה זה עוזר? למשל רציפות. תהי סדרת פונקציות רציפות. ניקח פונקציה f_n מהסדרה עבור n מספיק גדול, ונקח סביבה קטנה של x_0 כלשהו. מתוך רציפות, f_n שולחת את סביבה של x_0 קרוב מאד לf(x_0). אבל, f_n שולחת כל נקודה בסביבה לגובה קרוב מאד לפונקצית הגבול באותה נקודה כאשר המרחק לא תלוי בבחירת הנקודה. לכן גם כל הסביבה של פונקצית הגבול קרובה מאד לf(x_0( ויוצא שגם פונקצית הגבול רציפה.
שאלות
קודם כל, בקשר לאינטגרביליות. לפי הגדרת רימן, מותר לדלתא להיות תלויה במס' הקטעים - n?
- עוד שאלה. באחד המשפטים בכיתה, רוני כתב משהו כמו "g אינטגרבילית ולכן לכל אפסילון>0 קיימת דלתא, כך שלכל חלוקה T המקיימת שפרמטר החלוקה שלה קטן מדלתא, יתקיים: s(t) עליון פחות s(t) תחתון קטן מאפסילון (סליחה על הכתיבה המסורבלת..)
זה לא אמור להיות, שלכל אפסילון קיימת חלוקה 'אחת' T שמקיימת את זה? זה לא עירבוב של 2 הגדרות? תודה רבה (:
תשובה
מה זאת אומרת מותר לדלתא? יש פרמטר חלוקה - אורך הקטע הגדול ביותר. הסכומים מתכנסים אם על כל החלוקות החל מפרמטר חלוקה מספיק קטן (דלתא) הסכום קרוב לגבול עד כדי אפסילון. אין פה שום קשר למספר הקטעים בחלוקה. דלתא תלוי בלבד באפסילון, בפונקציה ובקטע.
קודם כל תבדיל בין הגדרה לבין משפט. הגדרה להתכנסות יש רק אחת. כל שאר התנאים להתכנסות שקולים.
בוודאי שאין חלוקה יחידה כזו, הרי כל עידון של החלוקה יקיים את התנאי גם כן. יכול להיות שבהוכחה שלו הוא יכל לרשום פחות דברים, אבל אין ספק שזה מוכיח.
- זה נכון שעידון של החלוקה יקיים את התנאי, אבל הוא טען שכל T שיקיים שפרמטר החלוקה שלו יהיה קטן מדלתא, יקיים את החלוקה. למה זה נכון? אני מסכים שלעידון זה יהיה נכון, אבל לא בהכרח לכל T כנ"ל.
- אני מניח שאחר כך הוא הוכיח שבמקרה המסויים זה מתקיים. כמו שאמרתי, יכול להיות שהוא הוכיח יותר ממה שצריך, אבל אם הוא הוכיח, מה רע? שנית, עבור פרמטר חלוקה מספיק קטן המרחק בין הסכום העליון לגבול והמרחק בין הסכום התחתון לגבול הם אפסילון חלקי שתים. לכן המרחק ביניהם הוא אפסילון.
- בקשר למשפט הראשון - הוא לא ניסה להוכיח כלום בהתחלה. הוא פשוט הסיק מהנתון, שאם G אינטגרלית אז בוודאי מתקיים מה שכתבתי למעלה..
- אוקיי. כמו שהסברתי, זה נכון.
- בקשר למשפט הראשון - הוא לא ניסה להוכיח כלום בהתחלה. הוא פשוט הסיק מהנתון, שאם G אינטגרלית אז בוודאי מתקיים מה שכתבתי למעלה..
- אני מניח שאחר כך הוא הוכיח שבמקרה המסויים זה מתקיים. כמו שאמרתי, יכול להיות שהוא הוכיח יותר ממה שצריך, אבל אם הוא הוכיח, מה רע? שנית, עבור פרמטר חלוקה מספיק קטן המרחק בין הסכום העליון לגבול והמרחק בין הסכום התחתון לגבול הם אפסילון חלקי שתים. לכן המרחק ביניהם הוא אפסילון.
שאלה
בתרגיל 3 פה: http://www.math.tau.ac.il/~boazslom/hedva2/Exercises/ex-02.pdf בפתרונות הם טוענים שמכיוון שf גזירה, ניתן להציב x=f(t). לא ממש הבנתי את הקשר, מישהו יכול להסביר?
תשובה
strictly monotonic כלומר מונוטונית ממש. זה התנאי לכך שתהיה לה הופכית ואז תוכל לבצע את ההצבה. כמובן שגם העובדה שהפונקציה גזירה נחוצה (על מנת שההופכית תהיה גזירה, חוץ אולי מנקודה אחת).
- אופס, התכוונתי לכתוב מונוטונית ממש מלכתחילה ובטעות כתבתי גזירה. בכל מקרה תודה רבה (:
שאלה
האם גזירה ברציפות משמעותה: 1)יש נגזרת 2)הנגזרת רציפה בלבד? תודה
תומר - כמו שאמרת - יש נגזרת והנגזרת הזו היא פונקציה רציפה .
ארז ותומר- אתם יכולים להגיד כבר מעכשיו אם יותר השימוש במחשבונים במבחן? בבקשה תרשו- מה אכפת לכם? זה לא יכול להזיק לכם, ואותנו זה מרגיע..... תודה.
- זה מבחן לא בוחן. החלטה של המרצים. מוזמנים לשאול אותם...
תומר - יש סיבה לא להרשות שימוש במחשבון ... יש שאלות שנראה ששימוש במחשבון יכול לעזור לפתור אותן ( כמו במועד ב בבוחן שהיה...) אבל פיתרון מבוסס על חישוב במחשבון לא התקבל ! הנימוקים צריכים להיות מבוססי הוכחה מתמטית ולא חישוב נקודתי .
ארז - מצטרף. מחשבון, מייפל, מטלב, וספרי לימוד הם כלים מאד חשובים למתמטיקאים. בשעת מבחן נבדקת היכולת המתמטית ללא חומרי עזר. שאלתי את רוני-יהיו מחשבונים.
בקשר למבחן שהעליתם
קודם כל, תודה רבה :) אבל לא מצאתי אלא שאלה אחת (אם בכלל) על כל החצי הראשון של הקורס, שחשוב לא פחות מהחצי השני (אינטגרלים לא אמיתיים, טורי חזקות וכו'). יש מבחנים שכוללים גם את החומר הזה? אם לא - האם הבוחן הוא אינדיקטור טוב להבנת החומר? כלומר, השאלות שם סה"כ מסכמות את החומר ברמה די גבוהה? ובנוסף, לגבי המועד ב' שהעליתם, שאלה אחת. הוכחנו לפי משפט לבג בדיוק את אותו המשפט, רק שלא נדרש שהנגזרת תהיה רציפה. למה דורשים את זה כאן? בכלל בפתרונות, הם אומרים שg*f (הרכבה) היא הרכבה של פונק' רציפות, אבל לא בטוח בכלל שf רציפה..
תשובה
איך היית מגדיר את שאלות 5 ו6 במועד א' ושאלה 5 במועד ב'?
אני רואה שהם למדו גם חומר שאנחנו לא למדנו, מן הסתם המבחן יהיה על מה שכן למדנו. אי אפשר להסיק ממבחן של שנה מסוימת בדיוק מה יהיה או לא יהיה במבחן. על מנת שמבחנים לא ימשכו שעות תמיד משמיטים חומר מסוים, והחומר הזה יכול להתחלף משנה לשנה וממועד למועד.
למעשה, אי אפשר בכלל לדעת מראש מה יהיה במבחן :)
לגבי השאלה השנייה, יכול להיות שהם לא לימדו לבג בשנה שעברה, ולכן נתנו שאלה חלשה יותר אבל פתירה.
שנית, אתה צודק f אינה רציפה, אחרת זו שאלה טריוויאלית לחלוטין (כל פונקציה רציפה על קטע סגור אינטגרבילית שם)
- תראו איזה מהירות, שלחתי לרוני את הבעייה שרשמת, והוא כבר החזיר לי גרסא מתוקנת. העלאתי אותה...
- תודה רבה :). בכל מקרה, אני רוצה לומר תודה על כל הפורום הזה וההשקעה האינסופית..
תרגיל
- נגדיר
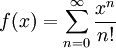 . הוכיחו ש
. הוכיחו ש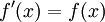
(לא ארז/תומר) קודם כל- זהו טור חזקות שמתכנס במ"ש לכל x ממשי. לכן ניתן לגזור איבר איבר.
ואז.
השוויון השני נכון כי עבור n=0 נקבל אפס. בשוויון הלפני אחרון החלפתי משתנה: 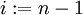
- זה שאתה לא אני זה לא מפתיע, כי אני רשמתי את השאלה :) רק דילגת על חלק עיקרי בהוכחה, מדוע הטור מתכנס במ"ש לכל x ממשי? זה נכון בכלל?
(מישהו אחר) זה נכון כי לפי המבחן של קושי עם הגבול העליון, הגבול של שורש nי של n! הוא אינסוף, ולכן הגבול של 1 חלקי זה הוא 0, ולכן הרדיוס הוא אינסוף. ואז אפשר להמשיך כמו שהבחור הקודם הראה, או להראות שan שווה בדיוק לפיתוח לטור חזקות של e^x שמקימת שהנגזרת שווה לפונקציה
- נתבונן בפונקציה
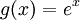 בקטע הסגור
בקטע הסגור ![[-r,r]](/images/math/4/1/b/41b4ab49507fdfa895adf70e230ce557.png) .
.
- נתבונן בפונקציה
לכל x בקטע ולכל n טבעי מתקיים
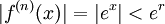
לכן בכל קטע סגור כזה ניתן לפתח את הפונקציה לטור חזקות, שזה בדיוק הטור בשאלה. הטור מתכנס בכל קטע סגור כזה, לכן הוא מתכנס (נקודתית) על כל הישר הממשי, כלומר יש לו רדיוס התכנסות אינסוף. לכן הוא מתכנס במ"ש בכל קטע סגור על הישר. לכן ניתן לגזור איבר איבר כמו למעלה.
- אי אפשר להשתמש בפיתוח של e^x ובעובדה שהוא הנגזרת של עצמו, הרי זה מה שאתם מתבקשים להוכיח.
- רדיוס ההתכנסות הוא אכן אינסוף ולכן טור החזקות מתכנס במ"ש על כל קטע סופי, ולכן מותר לגזור איבר איבר על כל קטע סופי. זו אכן התשובה. (זה לא אומר שהטור מתכנס במ"ש על כל הממשיים).
למה אי אפשר? אם אני מראה שאת e^x אפשר לפתח לטור חזקות והרדיוס התכנסות שלו זה אינסוף, ומראה שהטור חזקות זה בדיוק הטור הזה. זה לא אומר שהנגזרת שווה לפונקציה כמו e^x?
- הנחת שהנגזרת של e^x הינה e^x כאשר הראת שהטור הזה הוא הפיתוח של e^x. אבל זה מה שצריך להוכיח...
- איך מראים שרדיוס ההתכנסות הוא אינסוף?
![\overline{\lim_{n\rightarrow \infty}} \frac{1}{\frac{1}{\sqrt[n]{n!}}}=\infty](/images/math/2/9/d/29db1bc016652dfee7d9223eff67d21a.png) מכיוון ש
מכיוון ש![\lim \sqrt[n]{n!}=\infty](/images/math/e/9/1/e919ed310773d28aa0944415b69ec4c8.png)
- יש לי סתם שאלה, בלי קשר לתרגיל הזה - אם, באותו אופן, היה יוצא שהרדיוס הוא 0, האם זה מספיק, וכל שנותר הוא לבדוק התכנסות בנק' x=0?
- מספיק בשביל מה? זה אומר שהטור לא מתכנס בשום מקום פרט לנקודה. לכן הוא לא רציף ולא גזיר ולא מעניין. אין מה לבדוק התכנסות בנקודה אפס, זה תמיד מתכנס שם לקבוע a_0
- אבל איך חישבת את הגבול הזה?
- זה תרגיל מאינפי אחד. אתה מקטין את חצי מהאיברים של n! לאחד, ואת החצי השני אתה מקטין לn/2 וסה"כ אתה מקבל
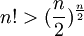 ולכן
ולכן ![\sqrt[n]{n!}>\sqrt[n]{(\frac{n}{2})^{\frac{n}{2}}}=\sqrt{\frac{n}{2}}\rightarrow \infty](/images/math/3/3/4/334384bff9671465545c55cd274a7f1c.png)
דבר אחר, ניתן להראות שלכל x0 ממשי טור המספרים שמתקבל ממנו מתכנס, ולכן הטור מתכנס נקודתית בכל הישר, ובפרט במ"ש בכל קטע סגור בו.
- איך התכנסות בכל נקודה גוררת התכנסות במ"ש? זה מאד לא נכון. ההתנכסות על כל קטע סופי היא במ"ש מכיוון שזה טור חזקות עם רדיוס אינסוף. טור חזקות מתכנס במ"ש על כל קטע סופי שקטן ממש מהרדיוס שלו.
-אבל אם הטור מתכנס בכל נקודה, זה בדיוק כמו לאמר שהרדיוס שלו הוא אינסוף...
- כן. אם זו הכוונה שלך אז אתה צודק. (חשוב לפרט שזה טור חזקות, ולכן הרדיוס הוא אינסוף ולכן הוא מתכנס במ"ש על כל קטע סופי).
-
- אפשר לומר שהגבול שצריך לחשב הוא הממוצע הגיאומטרי של הסדרה
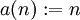 , ולכן שאיפת הסדרה לאינסוף גוררת את שאיפת הממוצע לאינסוף לפי משפט, לא?.
, ולכן שאיפת הסדרה לאינסוף גוררת את שאיפת הממוצע לאינסוף לפי משפט, לא?.
- אפשר לומר שהגבול שצריך לחשב הוא הממוצע הגיאומטרי של הסדרה
-
- אני לא זוכר משפט כזה, יכול להיות שאתה צודק..
שאלה - טורי חזקות
יש איזו נקודה שלא לגמרי נגענו בה בתרגול ההשלמה - טורי חזקות, כאשר החזקה היא, למשל, 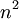 , או
, או 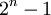 . מתי כדאי להפריד למקרים של מקדמים (ואז הסופרימום הוא מתי שיש מקדם), ומתי כדאי להציב, למשל,
. מתי כדאי להפריד למקרים של מקדמים (ואז הסופרימום הוא מתי שיש מקדם), ומתי כדאי להציב, למשל, 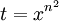 ? (בתרגיל יש רק דוגמא לזוגיים ואי-זוגיים)
? (בתרגיל יש רק דוגמא לזוגיים ואי-זוגיים)
- קשה קצת לענות בלי לראות דוגמא, צריך להשתמש בשיטה שבעזרתה תצליח לפתור את התרגיל.
- תומר - עשינו דוגמאות בהן למשל החזקות היו רק האי זוגיים למשל , והצגנו דרך להתייחסות למקרים כאלו - מופיע בסיכום תירגול ההשלמה הסרוק . בנוסף נשים לכם דוגמאות נוספות .
- אוקיי, יש לי דוגמא טובה - הטור:
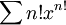 - כשפותרים אותו לפי מבחן השורש, מקבלים:
- כשפותרים אותו לפי מבחן השורש, מקבלים: 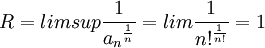
- אוקיי, יש לי דוגמא טובה - הטור:
(limsup זה גבול עליון)
- או מה לגבי :
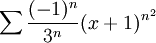 - אני הרי לא יכול לפרק את זה ל:
- אני הרי לא יכול לפרק את זה ל: 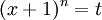 , אז אני חייב להגדיר את המקדמים כאפס כשזה לא "ריבוע שלם", וכ-
, אז אני חייב להגדיר את המקדמים כאפס כשזה לא "ריבוע שלם", וכ-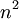 בריבוע שלם. במקרה הזה, כשמגדירים t=x+1, קבלתי: ש-
בריבוע שלם. במקרה הזה, כשמגדירים t=x+1, קבלתי: ש-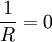 , ולכן זה תמיד מתכנס.
, ולכן זה תמיד מתכנס.
- או מה לגבי :
תשובה
לגבי הטור הראשון החישוב שלך נכון. בטור השני לא הבנתי איך פתרת אבל התשובה שגוייה. הרי אם תציב אפילו x=2 תקבל סדרה שאינה חסומה (ולכן וודאי הטור מתבדר. אבל אם תחשב שוב limsup תקבל:
![\limsup \sqrt[n^2]{|\frac{(-1)^n}{3^n}|} = \limsup \frac{1}{\sqrt[n]{3}} = 1](/images/math/3/e/5/3e5976a5b5a95f9f54f18e094e0d8f88.png) לכן רדיוס ההתכנסות הוא 1/1=1.
לכן רדיוס ההתכנסות הוא 1/1=1.
לכן הטור מתכנס עבור 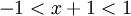 . מה הסיבה? הרי
. מה הסיבה? הרי 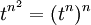 אם t>1 מתישהו t^n יהיה גדול מ3 ומאותו רגע הסדרה גדולה בערך מוחלט מאחד ולכן לא שואפת כלל לאפס.
אם t>1 מתישהו t^n יהיה גדול מ3 ומאותו רגע הסדרה גדולה בערך מוחלט מאחד ולכן לא שואפת כלל לאפס.
בקצוות הטור הראשון כמובן מתבדר אבל הטור השני מתכנס.
- אני מבין, ובחישוב שלי הגעתי לאותה תשובה, רק שמאיזשהי סיבה הייתי משוכנע ששלוש בחזקת אחת חלקיי אן שואף לאפס... תודה!
תרגיל 8 שאלה 2
בתרגיל 8 שאלה 2: לא היה אפשרי לפתור כך?: f רציפה ולכן יש לה קדומה,נסמנה g. האינטגרל של f מa עד b הוא בעצם הערך של g בנקודה b פחות ערכה בנקודה a. הפונקציה g היא גזירה, ולכן מתקיים עבודה תנאי לגראנז',(f היא הנגזרת של g): ולכן קיימת נקודה c עבורה ערך הפונקציה f בנקודה שווה לערך של g בנקודה b פחות ערכה בנקודה a חלקי b-a. מ.ש.ל.
לא יותר קל להוכיח ככה?
- זו הוכחה תקינה.
שאלה- לגבי נושאי הקורס שהעלתם
האם למדנו בקורס את פונקציה בעלת השתנות חסומה, ומשפט ז'ורדן? לא זכור לי שלמדנו...
- הקבוצה של רוני למדה. הקבוצה של שיין לא?
למיטב ידיעתי, ולאחר בדיקה בקלסר, לא למדנו את שני הנושאים הנ"ל, אשמח אם עוד מישהו יוכל לאשר זאת...
אכן, לא למדנו את הנושאים האלו.
אז מה נסגר? האם החומר ירד מהמבחן? לא נוכל ללמוד אותו לבד?! נשמח לקבל עדכון בעניין... תודה!
- מה שלא למדתם בהרצאה, לא יופיע במבחן.
במבחן שהועלה לאתר, במועד ב', לא היה אפשרי ויותר קל לפתור בדרך הבאה?:
הפונקציה רציפה ולכן חסומה- כמו שכתוב בפתרון.
ואז- אם הפונקציה רציפה בקטע סגור ולכן חסומה- אז נסמן בp את ההפרש בין הערך הכי גדול לערך הכי קטן שלה. ואז צריך להוכיח שלכל a>0 ולכל חלוקה T קיים r שגדול מדלתא T כך ש:סיגמה, כאשר i רץ מ1 עד n של Mi-mi כפול דלתא Xi קטן מa, נכון?
ואז נגיד שMi-mi קטן מp ודלתא Xi קטן מr. ולכן הסיגמה היא בעצם קטנה מ- n*r*p. ולכן נבחר את r להיות a/n*p. ואז זה שווה לa וסיימנו. שיניתי את האותיות המקובלות אבל זה אותה כוונה....
ההוכחה הזאת לא אומרת שכל פונקציה חסומה היא אינטגרבילית??? משהו כאן בטוח לא נכון, אבל מה? גם פונקצית דיריכלה יוצאת כאן אינטגרבילית, פשוט להציב p=1.......
- אני לא לגמרי מצליח לעקוב אחרי דרך הרישום הזו אבל:
- הכותב מעליי צודק, כביכול הוכחת שכל חסומה היא אינטגרבילית
- אני חושב שהבעייה היא שאתה מגדיר את r להיות תלוי בn. אני לא בטוח מה זה r אבל אני דיי בטוח שהוא לא צריך להיות תלוי בn :)
r הוא דלתא, המספר שגדול מאורך הקטע הגדול ביותר של החלוקה T.... מה הבעיה בלהגדיר אותו תלוי במספר האיברים בחלוקה T?
- כי ההגדרה לגבול סכומי רימן תלוייה בלבד בפרמטר החלוקה ואין קשר למספר הקטעים בחלוקה.
שאלה
תהי f פונקציה רציפה ב[a,b] ונניח שקיימת חלוקה P של [a,b] שעבורה הסכום העליון שווה לאינטגרל מa עד B של הפונקציה. צריך להראות כי בהכרח f קבועה ב[a,b]. רעיון ?
- נניח בשלילה שפונקציה אינה קבועה. נותר להראות שאם קיימת חלוקה כזו, קיים עידון שלה בעל סכום עליון קטן ממש יותר בסתירה.
- (לא ארז/תומר)אם אתה רוצה הוכחה מלאה: נתבונן בקטע החלוקה ה-i-י. נניח בשלילה שקיימת בקטע זה נקודה שערך הפונקציה בה קטן ממש מערך הפונקציה המקסימלי בקטע. ערך הפונקציה בכל x בקטע קטן שווה לערך המקסימום בקטע, וכיוון שיש נקודה בה אי השיוויון חזק, נקבל בתוספת הנתון על הרציפות שיש אי שיוויון חזק באינטגרלים. כלומר, אינטגרל על הערך המקסימלי גדול ממש מאינטגרל על הפונקציה, בקטע המדובר. כיוון שבכל קטע חלוקה אחר מתקיים שערך הפונקציה המקסימלי באותו קטע גדול שווה לכל ערך אחר בקטע (לפי הגדרת המקסימום, שקיים כי זו פונקציה רציפה בקטע סגור), אם נסכום את כל אי השוויונות האלו בתוספת אי השוויון החזק בקטע ה-i-י, נקבל שהאינטגרל על הפונקציה ב [a,b] קטן ממש מהסכום העליון של החלוקה P, בסתירה לנתון. לכן בקטע ה-i-י החלוקה קבועה. זה נכון לכל i ולכן בכל אחד מקטעי החלוקה הפונקציה קבועה. כעת נתבונן בנקודות החלוקה של P. לכל נקודה כזו (חוץ מהקיצוניות) מתקיים שהגבול של הפונקציה כש-x שואף לנקודה מימין הוא הערך הקבוע של הפונקציה בקטע שמימין לנקודה. ובאותו אופן הגבול משמאל יהיה הערך הקבוע בקטע שמשמאל לנקודה. הפונקציה רציפה בפרט בנקודות החלוקה, לכן הגבולות החד-צדדיים שווים כלומר הערכים הקבועים של הפונקציה בקטעי החלוקה הימני והשמאלי לנקודה שווים. זה נכון לכל נקודה בחלוקה ולכן הפונקציה קבועה. מש"ל.
- קודם כל, תודה רבה על ההשקעה! לא ממש הבנתי למה אתה מתכוון כשאתה אומר "כלומר, אינטגרל על הערך המקסימלי.." מה הכוונה?
- הוא מתכוון (אני מניח) לאינטגרל על הפונקציה הקבועה שערכה הוא ערך המקסימום שהפונקציה מקבלת
- ממש ממש תודה! :) עזרתם לי מאוד.
שאלה- גזירת טור חזקות
הוכחנו בהרצאה משפט שאומר שניתן לגזור טור חזקות איבר-איבר בכל נקודה בתחום התכנסותו. הניסוח של המשפט לא דורש התכנסות במ"ש, רק עושים בזה שימוש בהוכחה. לאור המשפט הזה- האם בתרגיל שהועלה לאתר (שצריך להוכיח שהפונקציה שווה לנגזרת), אפשר פשוט לגזור איבר איבר (כי זה טור חזקות)?
תשובה
יש בזה משהו, כי הרי כל נקודה בתחום ההתכנסות של טור חזקות מוכלת בסביבה סגורה בה ההתכנסות הינה במ"ש. (אני לא בטוח מה קורה אבל באופן כללי בנקודות הקצה של ההתכנסות, עם הנגזרת החד צדדית. במקרה שלנו זה לא משנה כי ההתכנסות הייתה בכל הממשיים)
התרגיל היה המצאה שלי על מנת לתרגל אתכם, המשפט שאתה מדבר עליו הוא מה שרציתי שתראו בתכלס...
שאלה
נתונה פונק' f החסומה ב[a,b]. הוכח כי אם f(x) אינטגרבילית ב[a,b] אז גם f^2(x) אינטגרבילית שם. זה לא נובע ישירות מהמשפט לגבי מכפלת פונק' אינטגרביליות?
תשובה
לא בטוח באיזה הקשר הגיעה השאלה, אבל דרך אחרת לפתור אותה היא לומר שזו הרכבה של הרציפה x^2 על פונקציה אינטגרבילית
- כן, אבל אין שום משפט על הרכבת פונ'...
- לימדנו אתכם את זה בתרגיל
אינטגרל לא אמיתי מסוג ראשון
איך ניתן להוכיח שהאינטגרל מ1 עד אינסוף, של x^a * sin(x) qqqq כאשר a הוא פרמטר שגדול מ0, הוא מתבדר?
תשובה
אפשר למשל לפי מבחן קושי להתכנסות טורים. הרי x^a שואף לאינסוף, והsin גדול מאיזה ערך חיובי באינסוף קטעים באורך קבוע. לכן כל אינטגרל על הקטעים האלה ישאף לאינסוף בסתירה לתנאי קושי.
- מבחן קושי להתכנסות טורים? כלומר, להשתמש במבחן האינטגרל?
- לא מבחן האינטגרל. הכוונה היא שהחל מM מספיק גדול כל אינטגרל מסויים על הפונקציה בין a,b>M קטן מאפסילון
- כשאני חושב על זה אולי אפשר לפתור את זה יותר בקלות עם מבחן ההשוואה הגבולי
- מבחן קושי להתכנסות טורים? כלומר, להשתמש במבחן האינטגרל?
(לא ארז/תומר) דבר ראשון, אני לא בטוח שאפשר לעשות פה מבחון ההשוואה הגבולי בכלל, כי ה- sin גורם שזו בכלל לא פונקצייה אי שלילית ב-R.. ובנוגע לפתרון, אני לא בטוח אם לזה התכוון מי שכתב על קריטריון קושי (וגם אם כן, אז אני לא בטוח שמה שהוא כתב כ"כ ברור) אז אני אראה את איך שאני חשבתי לפתור את זה- יהי E>0 ולכל M>0: נתבונן בפונקצייה f(x)=x^a*sin(x בקטע [2k*pi ,2k*pi+pi/4] כשלכל M חיובי יש קטע כזה כך שכל x בקטע גדול ממנו, ונשים לב לב לישר שעובר בנקודות x=2k*pi+pi/4,2k*pi ולא רק שהשטח שהוא יוצר עם ציר ה-X שואף לאינסוף ולכן בפרט גדול (החל מ-K מסויים) מ-E אלא גם שניתן להראות (ע"י גזירה ובדיקה פשוטה) כי לכל נקודה בקטע מתקבל ש f(x)-g(x) גדול שווה מ-0* ובסה"כ לפי קריטריון קושי הראינו שהאינטגרל בלא אמיתי מ-1 עד אינסוף מתבדר
- כש g הוא הישר שמחבר בין שתי נקודות הקצה..
שאלה
איך אפשר להוכיח שהפוקנצייה שמייצגת את האינטגרל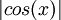 חסומה? (או אפילו לחשב את האינטגרל הזה)
חסומה? (או אפילו לחשב את האינטגרל הזה)
תשובה
היא לא חסומה, והאינטגרל דיי פשוט לחישוב. פשוט צריך להפריד למקרים בהם הקוסינוס שלילי והמקרים בו הוא חיובי.
- היא כן חסומה - הרצתי במייפל, וקבלתי שזה שווה ל:
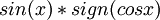 (וזה נראה הגיוני גם לפי ההפרדה למקרים)
(וזה נראה הגיוני גם לפי ההפרדה למקרים)
- אבל השטח מתחת ל'גבעה' של קוסינוס הוא ערך מסוים, אם תסכום אינסוף כאלה תקבל אינסוף. לכן הקדומה אינה חסומה. איפה הטעות שלך לדעתך?
- הבנתי, אתה צודק! תראה, התרגיל המקורי שלי הוא חישוב האינטגרל :
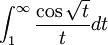 , ואחרי הצבה קבלתי שזה שווה לפעמיים האינטגרל:
, ואחרי הצבה קבלתי שזה שווה לפעמיים האינטגרל: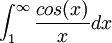 , וזה כמובן מתכנס לפי דיריכלה. עכשיו נשאר לי לבדוק התכנסות בהחלט, ואני לא יודע איך לעשות את זה
, וזה כמובן מתכנס לפי דיריכלה. עכשיו נשאר לי לבדוק התכנסות בהחלט, ואני לא יודע איך לעשות את זה
- הבנתי, אתה צודק! תראה, התרגיל המקורי שלי הוא חישוב האינטגרל :
- רק על מנת שכולם ידעו - הבעייה בפונקציה הקדומה שהצעת היא שהפונקציה
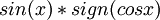 אינה רציפה. משמאל ל
אינה רציפה. משמאל ל היא אחד ומימין מינוס אחד. על מנת שהיא תהיה רציפה צריך להוסיף מספר שלם לכל 'מדרגה' כזו ואז הפונקציה אכן לא תהיה חסומה.
היא אחד ומימין מינוס אחד. על מנת שהיא תהיה רציפה צריך להוסיף מספר שלם לכל 'מדרגה' כזו ואז הפונקציה אכן לא תהיה חסומה.
- רק על מנת שכולם ידעו - הבעייה בפונקציה הקדומה שהצעת היא שהפונקציה
- בקשר לאינטגרל, ראה תרגיל 9 שאלה 6
שאלה
באינטגרלים לא אמיתיים: אפשר לומר שהאינטגרל של f+g [באותו תחום כמובן] שווה לאינטגרל של f ועוד האינטגרל של g?
ושהאינטגרל של g ב[a,b] + האינטגרל של g ב[b,c] שווה לאינטגרל מa עד b? (נניח שאחד מהם לא אמיתי)
תשובה
אם כולם מתכנסים אז כן
שאלה
בתרגיל 11 , הלינקים ששמתם שם לא עובדים. יש סיכוי שתוכלו לפרסם פה לינקים תקינים?
http://ocw.openu.ac.il/opus/Static/binaries/Upload/Bank116/mmn-16_0.pdf
http://ocw.openu.ac.il/opus/Static/binaries/Upload/Bank116/solution-16_0.pdf
(עדיף להעתיק את הלינקים ולא ללחוץ עליהם)
יש אפשרות לקבל את הפתרונות של תרגיל 11?