אי-שוויון הממוצעים

"נהוג לומר כי אם פותרים בעיה מסוימת אחת באופן מסוים אז זה תיחכום, ואם פותרים שתיים בעזרת אותו רעיון אז זו כבר שיטה."

(אסטרטגיות לפתרון בעיות מתמטיות, פרופ' בנו ארבל.)

אי-שוויון הממוצעים

יהיו מספרים חיוביים [math]\displaystyle{ 0\lt a_1,...,a_n\in\mathbb{R} }[/math] אזי:

[math]\displaystyle{ \frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\leq \sqrt[n]{a_1\cdots a_n}\leq \frac{a_1+...+a_n}{n} }[/math]

כאשר משמאל מופיע הממוצע ההרמוני, במרכז הממוצע ההנדסי (גאומטרי) ומימין הממוצע החשבוני (אלגברי).

שיוויון מתקיים אם ורק אם כל המספרים שווים [math]\displaystyle{ a_1=...=a_n }[/math].

טענת עזר

ראשית, נוכיח את הטענה הבאה:

יהיו [math]\displaystyle{ x_1,...,x_n }[/math] ממשיים חיוביים המקיימים [math]\displaystyle{ x_1\cdots x_n=1 }[/math].

אזי [math]\displaystyle{ x_1+...+x_n\geq n }[/math], ושיוויון מתקיים אם ורק אם כולם שווים 1.

עבור n=1 הטענה טריוויאלית.

יהי n עבורו הטענה נכונה, ונוכיח אותה עבור n+1.

יהיו [math]\displaystyle{ x_1\lt ...\lt x_{n+1} }[/math] ממשיים חיוביים המקיימים [math]\displaystyle{ x_1\cdots x_{n+1}=1 }[/math].

כיוון ש[math]\displaystyle{ x_1 }[/math] הינו המספר הקטן ביותר, ואילו [math]\displaystyle{ x_{n+1} }[/math] הינו המספר הגדול ביותר נובע כי [math]\displaystyle{ x_1\leq 1 }[/math] ואילו [math]\displaystyle{ x_{n+1}\geq 1 }[/math].

נסמן [math]\displaystyle{ x_1\cdot x_{n+1}=y_n }[/math], אזי [math]\displaystyle{ x_2\cdots x_n\cdot y_n = 1 }[/math], ולפי הנחת האינדוקציה מתקיים כי [math]\displaystyle{ x_2+...+x_n+y_n\geq n }[/math] ושיוויון אם"ם כולם שווים 1.

לכן אם נוכיח [math]\displaystyle{ x_1+...+x_{n+1}-1\geq x_2+...+x_n+x_1\cdot x_{n+1} }[/math], נקבל [math]\displaystyle{ x_1+...+x_{n+1}-1\geq n }[/math].

כעת נוכיח את אי השיוויון הרצוי

[math]\displaystyle{ x_1+...+x_{n+1}-1\geq x_2+...+x_n+x_1\cdot x_{n+1} }[/math].

זה נכון אם"ם

[math]\displaystyle{ x_1+x_{n+1}-1\geq x_1\cdot x_{n+1} }[/math]

זה שקול לאי השיוויון

[math]\displaystyle{ (x_1-1)(x_{n+1}-1)\leq 0 }[/math]

הוא נכון כיוון ש[math]\displaystyle{ x_1\leq 1 }[/math] ואילו [math]\displaystyle{ x_{n+1}\geq 1 }[/math].

כעת שיוויון [math]\displaystyle{ x_1+...+x_{n+1}=n+1 }[/math] גורר כי [math]\displaystyle{ x_1+...+x_{n+1}-1= x_2+...+x_n+x_1\cdot x_{n+1}=n }[/math] ולכן [math]\displaystyle{ (x_1-1)(x_{n+1}-1)= 0 }[/math].

לכן [math]\displaystyle{ x_1=x_{n+1}=1 }[/math] וביחד עם הנחת האינדוקציה נקבל כי [math]\displaystyle{ x_2=...=x_n=1 }[/math].

הוכחת אי שיוויון הממוצעים

נגדיר [math]\displaystyle{ x_i=\frac{a_i}{\sqrt[n]{a_1\cdots a_n}} }[/math] ונבחין כי:

[math]\displaystyle{ x_1\cdots x_n = \frac{a_1}{\sqrt[n]{a_1\cdots a_n}}\cdots \frac{a_n}{\sqrt[n]{a_1\cdots a_n}}=1 }[/math]

לכן לפי טענת העזר נקבל כי:

[math]\displaystyle{ x_1+...+x_n = \frac{a_1+...+a_n}{\sqrt[n]{a_1\cdots a_n}}\geq n }[/math]

ולכן [math]\displaystyle{ \sqrt[n]{a_1\cdots a_n}\leq \frac{a_1+...+a_n}{n} }[/math] ושיוויון אם"ם [math]\displaystyle{ x_1=...=x_n=1 }[/math].

כלומר שיוויון אם"ם [math]\displaystyle{ a_1=...=a_n=\sqrt[n]{a_1\cdots a_n} }[/math]

כעת נציב את המספרים [math]\displaystyle{ \frac{1}{a_1},...,\frac{1}{a_n} }[/math] ונקבל כי:

[math]\displaystyle{ \sqrt[n]{\frac{1}{a_1}\cdots \frac{1}{a_n}}\leq \frac{\frac{1}{a_1}+...+\frac{1}{a_n}}{n} }[/math]

כלומר

[math]\displaystyle{ \frac{n}{\frac{1}{a_1}\cdots \frac{1}{a_n}}\leq \sqrt[n]{a_1\cdots a_n} }[/math]

ושיוויון אם"ם [math]\displaystyle{ \frac{1}{a_1}=...=\frac{1}{a_n} }[/math].

שימושים

דוגמאות גאומטריות

היקפי מלבן וריבוע בעלי שטח זהה

יהיו מלבן וריבוע בעלי שטח זהה, אזי היקף המלבן גדול מהיקף הריבוע.

נסמן את שטח הצורות בs, ואת צלעות המלבן ב[math]\displaystyle{ a\neq b }[/math].

אזי היקף המלבן הינו [math]\displaystyle{ 2(a+b) }[/math] ואילו היקף הריבוע הינו [math]\displaystyle{ 4\sqrt{s} }[/math].

לפי אי שיוויון הממוצעים נקבל כי:

[math]\displaystyle{ 2(a+b)=4\frac{a+b}{2}\gt 4\sqrt{ab}=4\sqrt{s} }[/math]

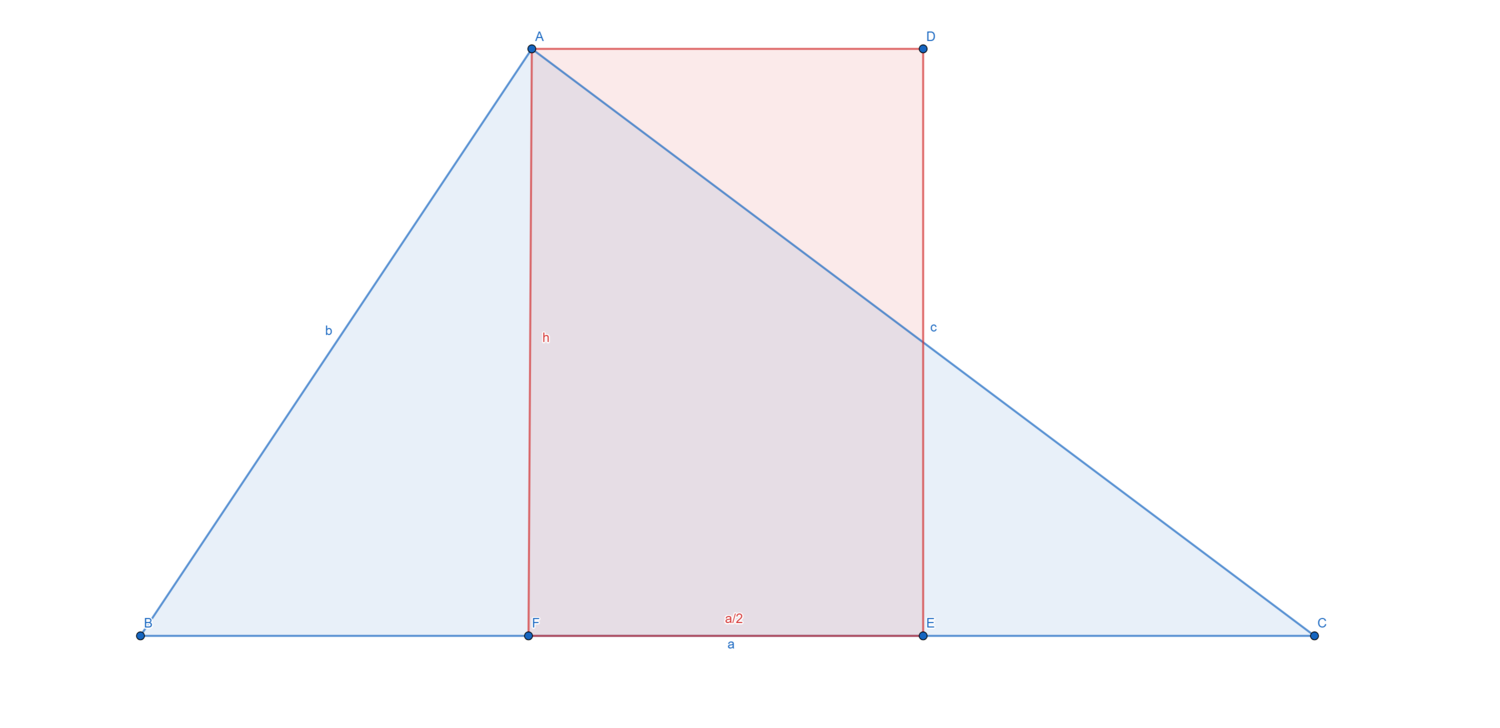
היקפי ריבוע ומשולש בעלי שטח זהה

יהיו משולש וריבוע בעלי שטח זהה, אזי היקף המשולש גדול מהיקף הריבוע.

נביט בבניית העזר הבאה:

(נבנה באמצעות גאוגברה.)

שטח המשולש זהה לשטח המלבן ושניהם שווים ל[math]\displaystyle{ \frac{h\cdot a}{2} }[/math].

היקף המשולש הינו [math]\displaystyle{ a+b+c }[/math] והיקף המלבן [math]\displaystyle{ 2(h+\frac{a}{2})=2h+a }[/math], שהוא כאמור גדול מהיקף הריבוע (או שווה לו במקרה ש[math]\displaystyle{ h=\frac{a}{2} }[/math]).

כעת צלעות המשלוש גדולות או שווה לגובה, ולפחות אחת מהן גדולה ממש (במקרה שמדובר במשולש ישר זוית, הגובה שווה לאחת הצלעות).

[math]\displaystyle{ a+b+c\gt h+h+a = 2h+a }[/math]

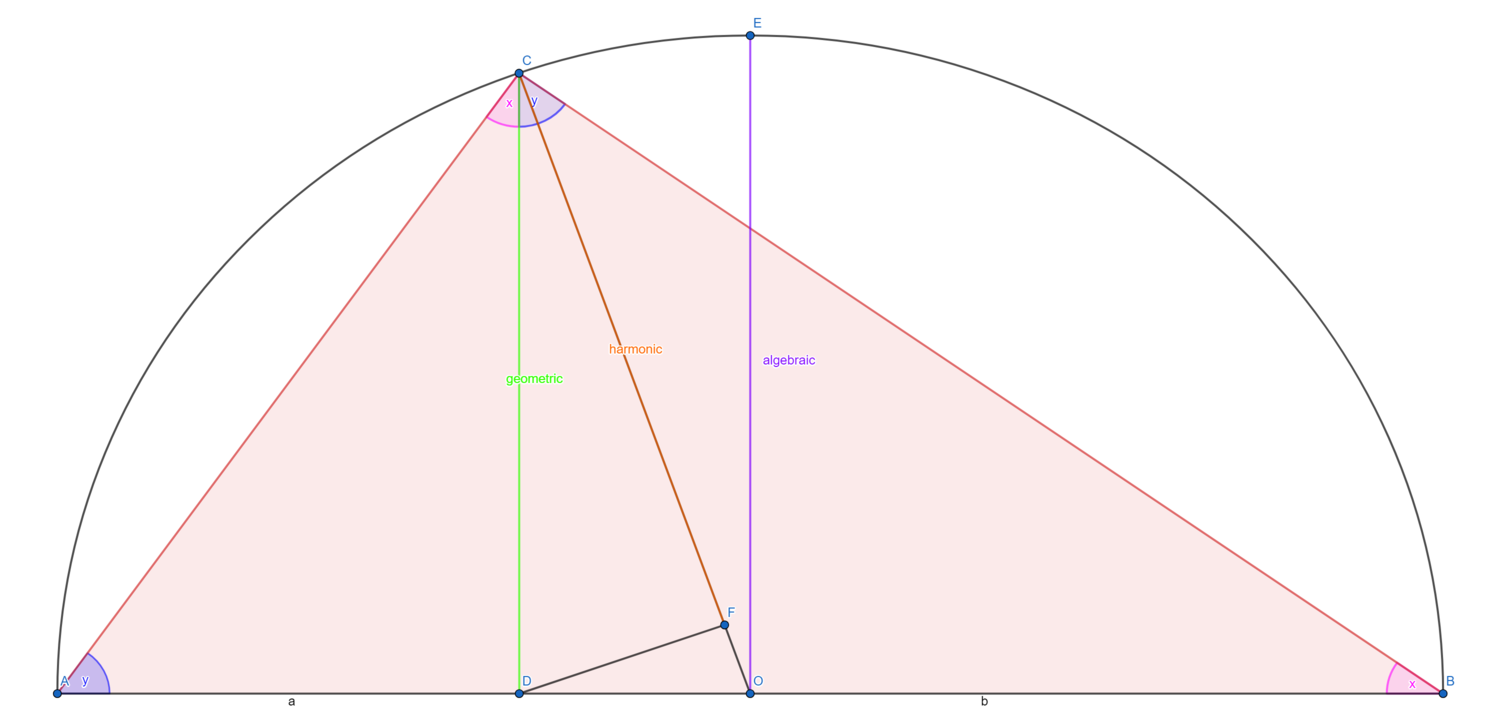
המחשה גאומטרית

נביט בשרטוט הבא:

(נבנה באמצעות גאוגברה.)

נניח כי אורך הקטע AD הינו a ואורך הקטע DB הינו b.

הנקודה O הינה מרכז המעגל, שרדיוסו [math]\displaystyle{ \frac{a+b}{2} }[/math] הרי הוא הממוצע החשבוני.

נרים את הגובה CD.

נשים לב כי הזוית C היא ישרה כיוון שהיא מונחת על הקוטר, ולכן המשולשים ADC ו CDB דומים.

מכאן [math]\displaystyle{ \frac{CD}{DB}=\frac{CD}{AD} }[/math].

לכן [math]\displaystyle{ CD^2=a\cdot b }[/math] וקיבלנו ש [math]\displaystyle{ CD=\sqrt{ab} }[/math] הרי הוא הממוצע ההנדסי.

לבסוף, נעביר גובה DF, ונקבל כי המשולשים CFD ו CDO דומים.

לכן [math]\displaystyle{ \frac{CF}{CD}=\frac{CD}{CO} }[/math]

ולכן [math]\displaystyle{ CF=\frac{CD^2}{CO}=\frac{ab}{\frac{a+b}{2}}=\frac{2}{\frac{1}{a}+\frac{1}{b}} }[/math] הרי הוא הממוצע ההרמוני.

משולש שווה צלעות

יהי משולש בעל צלעות באורך a,b,c.

הוכיחו כי המשולש שווה צלעות אם ורק אם [math]\displaystyle{ \frac{a}{b} + \frac{b}{c} + \frac{c}{a} =3 }[/math].

ראשית, [math]\displaystyle{ \sqrt[3]{\frac{a}{b} \cdot \frac{b}{c} \cdot \frac{c}{a}}\leq \frac{\frac{a}{b} + \frac{b}{c} + \frac{c}{a}}{3} }[/math] ושיוויון אם"ם כולם שווים.

לכן [math]\displaystyle{ \frac{a}{b} + \frac{b}{c} + \frac{c}{a} \geq 3 }[/math] ושיוויון רק אם [math]\displaystyle{ \frac{a}{b} = \frac{b}{c} = \frac{c}{a}=1 }[/math], כלומר [math]\displaystyle{ a=b=c }[/math]

כלל המנה

תהי סדרה חיובית [math]\displaystyle{ 0\lt a_n }[/math] כך ש [math]\displaystyle{ \frac{a_{n+1}}{a_n}\to L }[/math] אזי [math]\displaystyle{ \sqrt[n]{a_n}\to L }[/math].

הממוצע החשבוני

תהי סדרה [math]\displaystyle{ a_n\to L }[/math] אזי [math]\displaystyle{ \frac{a_1+...+a_n}{n}\to L }[/math].

כלומר הממוצע החשבוני של סדרה מתכנסת במובן הרחב, מתכנס לאותו הגבול.

הוכחה עבור [math]\displaystyle{ L\in \mathbb{R} }[/math]:

יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math].

קיים [math]\displaystyle{ n_1 }[/math] כך שלכל [math]\displaystyle{ n\gt n_1 }[/math] מתקיים כי [math]\displaystyle{ |a_n-L|\lt \frac{\varepsilon}{2} }[/math]

נסמן [math]\displaystyle{ M=|a_1-L|+...+|a_{n_1}-L| }[/math].

אזי [math]\displaystyle{ \left|\frac{a_1+...+a_n}{n}-L\right| = \left|\frac{(a_1-L)+...+(a_n-L)}{n}\right|\leq \frac{M+(n-n1)\frac{\varepsilon}{2}}{n}\leq\frac{M+n\frac{\varepsilon}{2}}{n} }[/math]

נבחר [math]\displaystyle{ n_2\gt n_1 }[/math] כך שלכל [math]\displaystyle{ n\gt n_2 }[/math] מתקיים כי [math]\displaystyle{ \frac{M}{n}\lt \frac{\varepsilon}{2} }[/math].

סה"כ, לכל [math]\displaystyle{ n\gt n_2 }[/math] מתקיים כי [math]\displaystyle{ \left|\frac{a_1+...+a_n}{n}-L\right|\lt \varepsilon }[/math] כפי שרצינו.

הוכחה עבור [math]\displaystyle{ L=\infty }[/math]:

יהי [math]\displaystyle{ M\gt 0 }[/math].

קיים [math]\displaystyle{ n_1 }[/math] כך שלכל [math]\displaystyle{ n\gt n_1 }[/math] מתקיים כי [math]\displaystyle{ a_n\gt 2M }[/math].

נסמן [math]\displaystyle{ x=a_1+...+a_{n_1} }[/math].

אזי [math]\displaystyle{ \frac{a_1+...+a_n}{n}\gt \frac{x+(n-n_1)2M}{n} = 2M + \frac{x-n_1}{n} }[/math]

נבחר [math]\displaystyle{ n_2\gt n_1 }[/math] כך שלכל [math]\displaystyle{ n\gt n_2 }[/math] מתקיים כי [math]\displaystyle{ \frac{x-n_1}{n}\gt -M }[/math]

וביחד נקבל כי לכל [math]\displaystyle{ n\gt n_2 }[/math] מתקיים [math]\displaystyle{ \frac{a_1+...+a_n}{n}\gt M }[/math]

הממוצע ההרמוני

תהי סדרה [math]\displaystyle{ 0\lt a_n\to L }[/math] אזי [math]\displaystyle{ \frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to L }[/math]

כלומר הממוצע ההרמוני של סדרה מתכנסת במובן הרחב, מתכנס לאותו הגבול.

שימו לב שדרשנו שהסדרה חיובית, אחרת ייתכן צמצום שיוביל לאפס במכנה.

הוכחה עבור [math]\displaystyle{ 0\neq L\in\mathbb{R} }[/math]:

[math]\displaystyle{ a_n\to L }[/math], לכן [math]\displaystyle{ \frac{1}{a_n}\to \frac{1}{L} }[/math].

לכן [math]\displaystyle{ \frac{\frac{1}{a_1}+...+\frac{1}{a_n}}{n}\to \frac{1}{L} }[/math]

ולכן [math]\displaystyle{ \frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to L }[/math]

הוכחה עבור [math]\displaystyle{ L=0 }[/math]:

[math]\displaystyle{ \frac{1}{a_n}\to \infty }[/math]

לכן [math]\displaystyle{ \frac{\frac{1}{a_1}+...+\frac{1}{a_n}}{n}\to \infty }[/math]

ולכן [math]\displaystyle{ \frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to 0 }[/math]

הוכחה עבור [math]\displaystyle{ L=\infty }[/math]:

[math]\displaystyle{ \frac{1}{a_n}\to 0 }[/math]

לכן [math]\displaystyle{ 0\lt \frac{\frac{1}{a_1}+...+\frac{1}{a_n}}{n}\to 0 }[/math]

ולכן [math]\displaystyle{ \frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to \infty }[/math]

הממוצע ההנדסי

לפי אי שיוויון הממוצעים, נובע כי אם [math]\displaystyle{ 0\lt a_n\to L }[/math] אזי [math]\displaystyle{ \sqrt[n]{a_1\cdots a_n}\to L }[/math]

הוכחת כלל המנה

תהי סדרה חיובית [math]\displaystyle{ 0\lt a_n }[/math] כך ש [math]\displaystyle{ \frac{a_{n+1}}{a_n}\to L }[/math].

נגדיר את הסדרה [math]\displaystyle{ b_n }[/math] ע"י [math]\displaystyle{ b_1=a_1 }[/math] ולכל [math]\displaystyle{ n\gt 1 }[/math] מתקיים [math]\displaystyle{ b_n=\frac{a_n}{a_{n-1}} }[/math]

לכן הממוצע ההנדסי של הסדרה [math]\displaystyle{ b_n }[/math] מקיים

[math]\displaystyle{ \sqrt[n]{a_1\cdot\frac{a_2}{a_1}\cdot\frac{a_3}{a_2}\cdots\frac{a_n}{a_{n-1}}}\to L }[/math]

לכן בעצם [math]\displaystyle{ \sqrt[n]{a_n}\to L }[/math] כפי שרצינו.

המספר e

נוכיח כי הסדרה [math]\displaystyle{ a_n=\left(1+\frac{1}{n}\right)^n }[/math] מונוטונית עולה ממש.

[math]\displaystyle{ \left(1+\frac{1}{n}\right)^n= \left(1+\frac{1}{n}\right)\cdots \left(1+\frac{1}{n}\right)\cdot 1 }[/math]

[math]\displaystyle{ \sqrt[n+1]{\left(1+\frac{1}{n}\right)^n}\lt \frac{\left(1+\frac{1}{n}\right)+...+\left(1+\frac{1}{n}\right)+1}{n+1}=\frac{n+2}{n+1}=1+\frac{1}{n+1} }[/math]

ולכן

[math]\displaystyle{ \left(1+\frac{1}{n}\right)^n\lt \left(1+\frac{1}{n+1}\right)^{n+1} }[/math]

נוכיח כי הסדרה [math]\displaystyle{ b_n=\left(1+\frac{1}{n}\right)^{n+1} }[/math] מונוטונית יורדת ממש.

[math]\displaystyle{ \sqrt[n+2]{\left(1+\frac{1}{n}\right)^{n+1}}\gt \frac{n+2}{\frac{1}{\left(1+\frac{1}{n}\right)} + ...+\frac{1}{\left(1+\frac{1}{n}\right)}+1 } }[/math]

[math]\displaystyle{ \left(1+\frac{1}{n}\right)^{n+1}\gt \left(\frac{n+2}{\frac{n+1}{1+\frac{1}{n}}+1}\right)^{n+2} = \left(\frac{n+2}{\frac{n+1}{\frac{n+1}{n}}+1}\right)^{n+2} =\left(\frac{n+2}{n+1}\right)^{n+2} = \left(1+\frac{1}{n+1}\right)^{n+2} }[/math]

לכן סה"כ לכל [math]\displaystyle{ n }[/math] מתקיים כי [math]\displaystyle{ a_1\lt a_n\lt b_n\lt b_1 }[/math] ושתי הסדרות מונוטוניות וחסומות ולכן מתכנסות.

נגדיר את המספר e להיות הגבול של הסדרה [math]\displaystyle{ a_n }[/math].

לכן [math]\displaystyle{ b_n=a_n\left(1+\frac{1}{n}\right)\to e\cdot 1 = e }[/math]

ומתקיים לכל n כי [math]\displaystyle{ a_n\lt e\lt b_n }[/math].

למשל עבור n=1 מקבלים כי [math]\displaystyle{ 2\lt e\lt 4 }[/math].

אי שיוויון ברנולי

יהי [math]\displaystyle{ \epsilon\gt -1 }[/math], אזי לכל [math]\displaystyle{ n\in\mathbb{N} }[/math] מתקיים כי [math]\displaystyle{ \left(1+\epsilon\right)^n\geq 1+n\cdot \epsilon }[/math]

אמנם לא מסובך במיוחד להוכיח את אי שיוויון ברנולי באינדוקציה, אנחנו נוכיח אותו באמצעות אי שיוויון הממוצעים.

למעשה באמצעות אי שיוויון הממוצעים, נוכיח גרסא רציונלית של אי השיוויון:

אם [math]\displaystyle{ \frac{m}{n}\geq 1 }[/math] אזי [math]\displaystyle{ \left(1+\epsilon\right)^{\frac{m}{n}}\geq 1 + \frac{m}{n}\cdot \epsilon }[/math]

ראשית, אם [math]\displaystyle{ 1+\frac{m}{n}\cdot\epsilon \lt 0 }[/math] אי השיוויון ברור.

לכן נניח כי [math]\displaystyle{ 1+\frac{m}{n}\cdot\epsilon\geq 0 }[/math].

לכן אי השיוויון שקול ל

[math]\displaystyle{ 1+\epsilon\geq \sqrt[m]{\left(1+\frac{m}{n}\epsilon\right)^n} }[/math]

כעת

[math]\displaystyle{ \sqrt[m]{\left(1+\frac{m}{n}\epsilon\right)^n\cdot 1^{m-n}}\leq \frac{n\cdot (1+\frac{m}{n}\epsilon) + (m-n)}{m} = 1+\epsilon }[/math]

שימוש באי שיוויון ברנולי

יהי [math]\displaystyle{ a\gt 1 }[/math] אזי [math]\displaystyle{ a^n\to \infty }[/math].

נסמן [math]\displaystyle{ a=1+\epsilon }[/math], כאשר [math]\displaystyle{ \epsilon\gt 0 }[/math].

לכן [math]\displaystyle{ a^n=(1+\epsilon)^n\geq 1+n\epsilon\to \infty }[/math].

יהי [math]\displaystyle{ 0\lt a\lt 1 }[/math] אזי [math]\displaystyle{ a^n\to 0 }[/math].

כיוון ש [math]\displaystyle{ 0\lt a\lt 1 }[/math] נובע כי [math]\displaystyle{ \frac{1}{a}\gt 1 }[/math].

לכן, [math]\displaystyle{ a^n = \frac{1}{\left(\frac{1}{a}\right)^n}\to \frac{1}{\infty}=0 }[/math]

אי שיוויון קושי-שוורץ

עבור [math]\displaystyle{ \mathbb{R}^n }[/math]

לכל [math]\displaystyle{ a_1,...,a_n,b_1,...,b_n\in\mathbb{R} }[/math] מתקיים

[math]\displaystyle{ |a_1b_1+...+a_nb_n|\leq \sqrt{a_1^2+...+a_n^2}\sqrt{b_1^2+...+b_n^2} }[/math]

קל לראות שמספיק להוכיח את הטענה למספרים אי שליליים, וכך נעשה.

ראשית, אם נציב את [math]\displaystyle{ x^2,y^2 }[/math] באי שיוויון הממוצעים נקבל [math]\displaystyle{ xy\leq \frac{x^2+y^2}{2} }[/math].

לכן,

[math]\displaystyle{ \sum_{k=1}^n x_ky_k\leq \frac{\sum_{k=1}^nx_k^2 + \sum_{k=1}^ny_k^2}{2} }[/math]

כעת נציב [math]\displaystyle{ x_k=\frac{a_k}{\sqrt{a_1^2+...+a_n^2}} }[/math] ו[math]\displaystyle{ y_k=\frac{b_k}{\sqrt{b_1^2+...+b_n^2}} }[/math] לכל k ונקבל

[math]\displaystyle{ \frac{\sum_{k=1}^n a_kb_k}{\sqrt{a_1^2+...+a_n^2}\sqrt{b_1^2+...+b_n^2}}\leq 1 }[/math]

וזהו בדיוק אי שיוויון קושי שוורץ.

עבור מכפלה פנימית כללית

האם אותה הוכחה מתרגמת עבור מכפלה פנימית כללית?

ובכן, [math]\displaystyle{ \langle v,w \rangle }[/math]

ביבליוגרפיה

• אסטרטגיות לפתרון בעיות מתמטיות, בנו ארבל.
• The Cauchy-Schwarz Master Class, J. Michael Steele.