אלגברה לינארית 1/הוכחות - דרגת שורות שווה דרגת עמודות
הוכחה שדרגת העמודות שווה לדרגת השורות
נזכור כי דרגת העמודות של מטריצה  היא מימד מרחב העמודות (המרחב הנפרש על ידי עמודות
היא מימד מרחב העמודות (המרחב הנפרש על ידי עמודות  ).
).
ודרגת השורות של מטריצה  היא מימד מרחב השורות (המרחב הנפרש על ידי שורות
היא מימד מרחב השורות (המרחב הנפרש על ידי שורות  ).
).
הוכחה לכך שדרגת העמודות של מטריצה שווה לדרגת השורות של מטריצה:
תהי 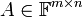 מטריצה כלשהיא ונניח שדרגת העמודות שלה היא
מטריצה כלשהיא ונניח שדרגת העמודות שלה היא  .
.
כלומר 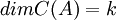 .
.
ההוכחה מחולקת לכמה שלבים.
שלב א': למצוא מטריצות 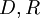 כך שמספר העמודות ב
כך שמספר העמודות ב 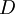 ומספר השורות ב
ומספר השורות ב  הם
הם  . ומתקיים
. ומתקיים 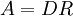 .
.
יהיה 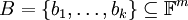 בסיס עבור
בסיס עבור 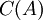 .
.
נסמן ב 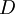 את המטריצה שעמודותיה הם איברי
את המטריצה שעמודותיה הם איברי  .
.
כלומר
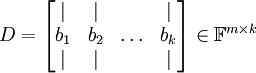
נשים לב שבגלל ש  בסיס ל
בסיס ל  הוא פורש כל עמודה של
הוא פורש כל עמודה של  .
.
כלומר לכל עמודה  מתקיים ש
מתקיים ש 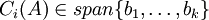 .
.
נסמן ![[C_i(A)]_B=\begin{bmatrix} \alpha_{1,i} \\ \alpha_{2,i} \\ \vdots \\ \alpha_{k,i} \end{bmatrix}](/images/math/1/9/7/197a5389dfa395310e515516883c55d9.png)
כלומר 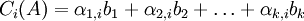
כלומר 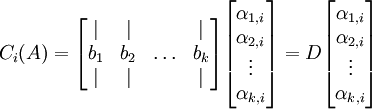
נגדיר מטריצה 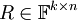 לפי
לפי
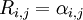 .
.
נשים לב ש הכפל 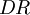 מוגדר היות ומספר העמודות ב
מוגדר היות ומספר העמודות ב 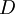 ומספר השורות ב
ומספר השורות ב  הם
הם  .
.
נקבל ש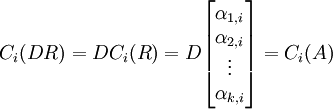
כלומר 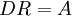 .
.
סוף שלב א'.
שלב ב': לראות ש 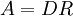 אומר שדרגת השורות של
אומר שדרגת השורות של  קטנה מדרגת השורות של
קטנה מדרגת השורות של  ולהסיק מסקנות.
ולהסיק מסקנות.
לפי כפל שורה שורה
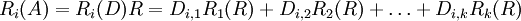
כלומר
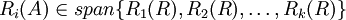
לכן 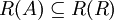
ולכן 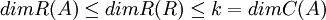
(מרחב השורות של המטריצה  לא יכול להיות יותר מ
לא יכול להיות יותר מ  כי יש ב
כי יש ב  רק
רק  שורות.)
שורות.)
זה מוכיח שלכל מטריצה  מתקיים ש
מתקיים ש 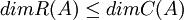 .
.
סוף שלב ב'
שלב ג': סיום.
נשים לב ש 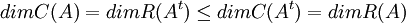
בסה"כ קיבלנו 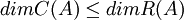 וגם
וגם 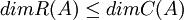 ולכן
ולכן
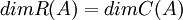 מש"ל.
מש"ל.