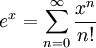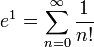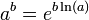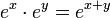הבדלים בין גרסאות בדף "פונקצית האקספוננט"
(יצירת דף עם התוכן "בערך זה נגדיר את פונקצית האקספוננט ונוכיח תכונות חשובות שלה. אמנם יש דרכים אחרות להגדיר...") |
(אין הבדלים)
|
גרסה מ־18:42, 20 ביוני 2021
בערך זה נגדיר את פונקצית האקספוננט ונוכיח תכונות חשובות שלה.
אמנם יש דרכים אחרות להגדיר את e וחזקות של מספרים, אנחנו נציג גרסא מבוססת על כלים מתקדמים (טורי חזקות) המתאימה גם לשדה המספרים המרוכבים.
הקדמה
לכל 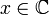 נגדיר את פונקצית האקספוננט
נגדיר את פונקצית האקספוננט
(קל לוודא כי טור החזקות הנ"ל מתכנס בכל שדה המרוכבים.)
נגדיר את המספר e להיות
הקוראים עשויים להזדעק ולומר שהסימון 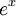 שמור לחזקה של שני מספרים; ובכן, אנחנו נגדיר חזקה של שני מספרים באמצעות האקספוננט ונוכיח את התכונות המוכרות של פעולת החזקה.
שמור לחזקה של שני מספרים; ובכן, אנחנו נגדיר חזקה של שני מספרים באמצעות האקספוננט ונוכיח את התכונות המוכרות של פעולת החזקה.
כלומר נגדיר לכל 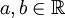 כך ש
כך ש 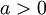 כי
כי
כאשר 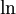 היא הפונקציה ההופכית לאקספוננט בממשיים. (כמובן שעלינו להוכיח כי פונקצית האקספוננט
היא הפונקציה ההופכית לאקספוננט בממשיים. (כמובן שעלינו להוכיח כי פונקצית האקספוננט 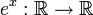 הפיכה.)
הפיכה.)
כפל אקספוננטים
אחת התכונות הבסיסיות והחשובות ביותר של האקספוננט היא
כיוון שעדיין לא הגדרנו חזקות, בוודאי לא ניתן להשתמש בחוקי חזקות על מנת להוכיח תכונה זו.
עלינו להוכיח אותה ישירות על ידי ההגדרה של האקספוננט כטור חזקות.