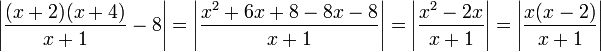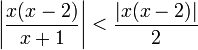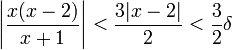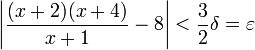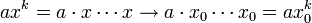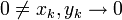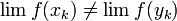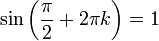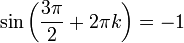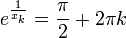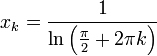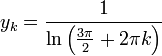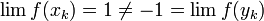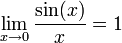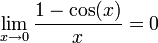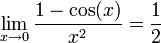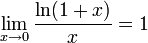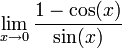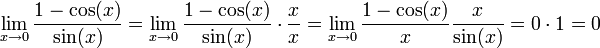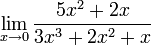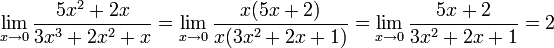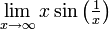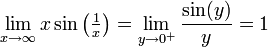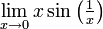הבדלים בין גרסאות בדף "גבול פונקציה"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
 
(2 גרסאות ביניים של אותו משתמש אינן מוצגות)
שורה 6: שורה 6:
 
<videoflash>Jp5FqgylIak</videoflash>
 
<videoflash>Jp5FqgylIak</videoflash>
  
−
<font size=4 color=#3c498e>'''הגדרה.''' </font>
+
;<font size=4 color=#3c498e>הגדרה.</font>
−
<math>L</math> נקרא '''הגבול של <math>f</math> בנקודה <math>a</math>''' אם <math>f</math> מוגדרת בסביבה מנוקבת של <math>a</math> וגם לכל <math>\epsilon>0</math> קיים <math>\delta>0</math> כך שלכל <math>x</math> המקיים <math>0<|x-a|<\delta</math> מתקיים <math>\Big|f(x)-L\Big|<\epsilon</math>
+
<math>L</math> נקרא '''הגבול של <math>f</math> בנקודה <math>a</math>''' אם <math>f</math> מוגדרת בסביבה מנוקבת של <math>a</math> וגם לכל <math>\varepsilon>0</math> קיים <math>\delta>0</math> כך שלכל <math>0<|x-a|<\delta</math> מתקיים <math>\Big|f(x)-L\Big|<\varepsilon</math> .
  
−
(הערה: סביבה מנוקבת של <math>a</math> הנה סביבה של <math>a</math> שמוציאים ממנה את <math>a</math>.)
+
(הערה: סביבה מנוקבת של <math>a</math> הנה סביבה של <math>a</math> שמוציאים ממנה את <math>a</math> .)
  
−
הסבר ההגדרה: לכל מרחק על ציר <math>y</math> שנבחר (אפסילון) יש מרחק על ציר <math>x</math> (דלתא) כך שאם הנקודות על ציר <math>x</math> קרובות מספיק ל- <math>a</math> אזי הפונקציה עליהן קרובה מספיק ל- <math>L</math> .
+
הסבר ההגדרה: לכל מרחק על ציר <math>y</math> שנבחר (אפסילון) יש מרחק על ציר <math>x</math> (דלתא) כך שאם הנקודות על ציר <math>x</math> קרובות מספיק ל-<math>a</math> אזי הפונקציה עליהן קרובה מספיק ל-<math>L</math> .
  
  
−
<font size=4 color=#a7adcd>'''תרגיל.''' </font>
+
;<font size=4 color=#a7adcd>תרגיל.</font>
−
הוכח לפי ההגדרה כי <math>\lim\limits_{x\to 2}\frac{(x+2)(x+4)}{x+1}=8</math>
+
הוכח לפי ההגדרה כי <math>\lim\limits_{x\to2}\dfrac{(x+2)(x+4)}{x+1}=8</math>
  
−
'''פתרון.'''
+
;פתרון
−
יהי <math>\epsilon>0</math> . צריך להוכיח כי קיים <math>\delta>0</math> , כך שאם <math>0<|x-2|<\delta</math> אזי מתקיים  
+
יהי <math>\varepsilon>0</math> . צריך להוכיח כי קיים <math>\delta>0</math> , כך שאם <math>0<|x-2|<\delta</math> אזי מתקיים  
−
<math>\left|\frac{(x+2)(x+4)}{x+1}-8\right|<\epsilon</math>
+
<math>\left|\dfrac{(x+2)(x+4)}{x+1}-8\right|<\varepsilon</math>
  
 
נפתח את הביטוי:
 
נפתח את הביטוי:
−
 
 
:<math>\left|\frac{(x+2)(x+4)}{x+1}-8\right|=\left|\frac{x^2+6x+8-8x-8}{x+1}\right|=\left|\frac{x^2-2x}{x+1}\right|=\left|\frac{x(x-2)}{x+1}\right|</math>
 
:<math>\left|\frac{(x+2)(x+4)}{x+1}-8\right|=\left|\frac{x^2+6x+8-8x-8}{x+1}\right|=\left|\frac{x^2-2x}{x+1}\right|=\left|\frac{x(x-2)}{x+1}\right|</math>
−
 
+
אנו רואים כי כאשר <math>x\to2</math> המונה שואף ל-0 והמכנה ל-3. נרצה, אם כך, לחסום את המכנה מלמטה על-ידי קבוע גדול מ-0, כך נוכל להקטין את המכנה, ולהגדיל את הביטוי.
−
 
+
−
אנו רואים כי כאשר <math>x\to 2</math> המונה שואף לאפס, והמכנה ל- <math>3</math> . נרצה, אם כך, לחסום את המכנה מלמטה על-ידי קבוע גדול מאפס, כך נוכל להקטין את המכנה, ולהגדיל את הביטוי.
+
  
 
כאשר <math>\delta<1</math> , עבור <math>0<|x-2|<\delta<1</math> מתקיים <math>2<x+1</math> ולכן:
 
כאשר <math>\delta<1</math> , עבור <math>0<|x-2|<\delta<1</math> מתקיים <math>2<x+1</math> ולכן:
−
:<math>\left|\frac{x(x-2)}{x+1}\right|<\frac{|x(x-2)|}{2}</math>
+
:<math>\left|\dfrac{x(x-2)}{x+1}\right|<\dfrac{|x(x-2)|}{2}</math>
 
כמו כן, מתקיים <math>x<3</math> ולכן:
 
כמו כן, מתקיים <math>x<3</math> ולכן:
−
:<math>\left|\frac{x(x-2)}{x+1}\right|<\frac{3|x-2|}{2}<\frac{3}{2}\delta</math>
+
:<math>\left|\dfrac{x(x-2)}{x+1}\right|<\dfrac{3|x-2|}{2}<\dfrac32\delta</math>
−
לסיכום, קיים דלתא כך ש- <math>\delta<1</math> וגם <math>\delta<\frac{2}{3}\epsilon</math> עבורו מתקיים:
+
לסיכום, קיים דלתא כך ש- <math>\delta<1</math> וגם <math>\delta<\dfrac23\varepsilon</math> עבורו מתקיים:
−
:<math>\left|\frac{(x+2)(x+4)}{x+1}-8\right|<\frac{3}{2}\delta=\epsilon</math>
+
:<math>\left|\dfrac{(x+2)(x+4)}{x+1}-8\right|<\dfrac32\delta=\varepsilon</math>
  
 
==גבול פונקציה לפי היינה==
 
==גבול פונקציה לפי היינה==
שורה 40: שורה 37:
 
בהגדרת קושי לגבול פונקציה הכללנו את הרעיון של גבול של סדרה, אך לא השתמשנו בו. בהגדרת הגבול לפי היינה נסתמך על הגדרת הגבול של סדרה.
 
בהגדרת קושי לגבול פונקציה הכללנו את הרעיון של גבול של סדרה, אך לא השתמשנו בו. בהגדרת הגבול לפי היינה נסתמך על הגדרת הגבול של סדרה.
  
 +
<font size=4 color=#3c498e>'''הגדרה.''' </font>
 +
<math>L</math> נקרא '''הגבול של <math>f</math> בנקודה <math>a</math>''' אם <math>f</math> מוגדרת בסביבה מנוקבת של <math>a</math> וגם לכל סדרה <math>x_n</math> המקיימת את שני התנאים הבאים:
 +
*<math>\forall n:x_n\ne a</math>
 +
*<math>\lim_{n\to\infty}x_n=a</math> (כאשר זהו גבול של סדרות)
  
−
<font size=4 color=#3c498e>
+
מתקיים כי הסדרה <math>f(x_n)</math> שואפת ל- <math>L</math> (שוב, גבול של סדרות).
−
'''הגדרה.'''
+
−
</font>
+
−
L נקרא '''הגבול של f בנקודה a''' אם f מוגדרת בסביבה מנוקבת של a וגם לכל סדרה <math>x_n</math> המקיימת את שני התנאים הבאים:
+
−
*<math>\forall n:x_n\neq a</math>
+
−
*<math>\lim_{n\rightarrow\infty}x_n=a</math> (כאשר זהו גבול של סדרות)
+
  
−
מתקיים כי הסדרה <math>f(x_n)</math> שואפת ל-L (שוב, גבול של סדרות).
+
<font size=4 color=#a7adcd>'''תרגיל.'''</font>
−
 
+
−
<font size=4 color=#a7adcd>
+
−
'''תרגיל.'''  
+
−
</font>
+
−
 
+
−
הוכח כי <math>\lim_{x\rightarrow x_0}ax^k=ax_0^k</math>
+
  
 +
הוכח כי <math>\lim\limits_{x\to x_0}ax^k=ax_0^k</math>
  
 
'''פתרון.'''
 
'''פתרון.'''
−
לכל סדרה <math>x_0\neq x_n\rightarrow x_0</math> מתקיים לפי אריתמטיקת גבולות של סדרות כי  
+
לכל סדרה <math>x_0\ne x_n\to x_0</math> מתקיים לפי אריתמטיקת גבולות של סדרות כי
 +
:<math>ax^k=a\cdot x\cdots x\to a\cdot x_0\cdots x_0=ax_0^k</math>
  
−
::<math>ax^k=a\cdot x \cdots x\rightarrow a\cdot x_0 \cdots x_0 = ax_o^k</math>
+
'''מסקנה.''' קל להראות כי לכל פולינום p מתקיים <math>\lim\limits_{x\to x_0}p(x)=p(x_0)</math>
  
 +
<font size=4 color=#a7adcd>'''תרגיל.'''</font>
  
−
'''מסקנה.''' קל להראות כי לכל פולינום p מתקיים <math>\lim_{x\rightarrow x_0}p(x)=p(x_0)</math>
+
הוכח כי לא קיים הגבול <math>\lim\limits_{x\to 0}\sin(e^{\frac{1}{x}})</math>
−
 
+
−
<font size=4 color=#a7adcd>
+
−
'''תרגיל.'''
+
−
</font>
+
−
 
+
−
הוכח כי לא קיים הגבול <math>\lim_{x\rightarrow 0}sin(e^{\frac{1}{x}})</math>
+
−
 
+
  
 
'''הוכחה.''' נראה כי קיימות סדרות
 
'''הוכחה.''' נראה כי קיימות סדרות
−
::<math>0\neq x_k,y_k\rightarrow 0</math>
+
:<math>0\ne x_k,y_k\to 0</math>
−
 
+
−
כך ש
+
−
::<math>\lim f(x_k)\neq \lim f(y_k)</math>
+
  
 +
כך ש-
 +
:<math>\lim f(x_k)\ne\lim f(y_k)</math>
  
 
נזכר בעובדה שלכל מספר שלם k מתקיים:
 
נזכר בעובדה שלכל מספר שלם k מתקיים:
−
::<math>sin\Big(\frac{\pi}{2}+2\pi k\Big)=1</math>
+
:<math>\sin\left(\frac{\pi}{2}+2\pi k\right)=1</math>
−
 
+
−
::<math>sin\Big(\frac{3\pi}{2}+2\pi k\Big)=-1</math>
+
−
 
+
  
 +
:<math>\sin\left(\frac{3\pi}{2}+2\pi k\right)=-1</math>
 
נרצה סדרה המקיימת
 
נרצה סדרה המקיימת
−
 
+
:<math>e^\frac{1}{x_k}=\frac{\pi}{2}+2\pi k</math>
−
::<math>e^{\frac{1}{x_k}}=\frac{\pi}{2}+2\pi k</math>
+
−
 
+
 
ולכן ניקח
 
ולכן ניקח
−
 
+
:<math>x_k=\frac{1}{\ln\Big(\frac{\pi}{2}+2\pi k\Big)}</math>
−
::<math>x_k=\frac{1}{ln\Big(\frac{\pi}{2}+2\pi k\Big)}</math>
+
−
 
+
 
באופן דומה ניקח
 
באופן דומה ניקח
−
::<math>y_k=\frac{1}{ln\Big(\frac{3\pi}{2}+2\pi k\Big)}</math>
+
:<math>y_k=\frac{1}{\ln\Big(\frac{3\pi}{2}+2\pi k\Big)}</math>
−
 
+
−
 
+
 
ואז נקבל  
 
ואז נקבל  
−
 
+
:<math>\lim f(x_k)=1\ne -1=\lim f(y_k)</math>
−
::<math>\lim f(x_k)=1\neq -1 =\lim f(y_k)</math>
+
  
 
==גבולות ידועים==
 
==גבולות ידועים==
−
::<math>\lim_{x\rightarrow 0}\frac{sin(x)}{x}=1</math>
+
:<math>\lim_{x\to 0}\frac{\sin(x)}{x}=1</math>
  
 +
:<math>\lim_{x\to 0}\frac{1-\cos(x)}{x}=0</math>
  
−
::<math>\lim_{x\rightarrow 0}\frac{1-cos(x)}{x}=0</math>
+
:<math>\lim_{x\to 0}\frac{1-\cos(x)}{x^2}=\frac{1}{2}</math>
  
−
 
+
:<math>\lim_{x\to 0}\frac{\ln(1+x)}{x}=1</math>
−
::<math>\lim_{x\rightarrow 0}\frac{1-cos(x)}{x^2}=\frac{1}{2}</math>
+
−
 
+
−
 
+
−
::<math>\lim_{x\rightarrow 0}\frac{ln(1+x)}{x}=1</math>
+
  
 
==דוגמאות==
 
==דוגמאות==
 
חשב את הגבולות הבאים:
 
חשב את הגבולות הבאים:
−
 
+
*<math>\lim_{x\to 0}\frac{1-\cos(x)}{\sin(x)}</math>
−
*<math>\lim_{x\rightarrow 0}\frac{1-cos(x)}{sin(x)}</math>
+
−
 
+
−
 
+
 
'''פתרון''':
 
'''פתרון''':
−
 
+
:<math>\lim_{x\to 0}\frac{1-\cos(x)}{\sin(x)}=\lim_{x\to 0}\frac{1-\cos(x)}{\sin(x)}\cdot\frac{x}{x}=\lim_{x\to 0}\frac{1-\cos(x)}{x}\frac{x}{\sin(x)}=0\cdot 1=0</math>
−
::<math>\lim_{x\rightarrow 0}\frac{1-cos(x)}{sin(x)}=\lim_{x\rightarrow 0}\frac{1-cos(x)}{sin(x)}\cdot\frac{x}{x} = \lim_{x\rightarrow 0}\frac{1-cos(x)}{x}\frac{x}{sin(x)}=0\cdot 1 = 0</math>
+
−
 
+
−
 
+
−
 
+
−
*<math>\lim_{x\rightarrow 0}\frac{5x^2+2x}{3x^3+2x^2+x}</math>
+
  
  
 +
*<math>\lim_{x\to 0}\frac{5x^2+2x}{3x^3+2x^2+x}</math>
 
'''פתרון''':
 
'''פתרון''':
−
 
+
:<math>\lim_{x\to 0}\frac{5x^2+2x}{3x^3+2x^2+x}=\lim_{x\to 0}\frac{x(5x+2)}{x(3x^2+2x+1)}=\lim_{x\to 0}\frac{5x+2}{3x^2+2x+1}=2</math>
−
::<math>\lim_{x\rightarrow 0}\frac{5x^2+2x}{3x^3+2x^2+x}=\lim_{x\rightarrow 0}\frac{x(5x+2)}{x(3x^2+2x+1)}=\lim_{x\rightarrow 0}\frac{5x+2}{3x^2+2x+1}=2</math>
+
  
 
'''הערה''': שימו לב שכאשר המשתנה שואף לאפס, החזקה המשמעותית היא דווקא '''הנמוכה''' בניגוד לכאשר המשתנה שואף לאינסוף.
 
'''הערה''': שימו לב שכאשר המשתנה שואף לאפס, החזקה המשמעותית היא דווקא '''הנמוכה''' בניגוד לכאשר המשתנה שואף לאינסוף.
  
  
−
*<math>\lim_{x\rightarrow \infty}xsin\Big(\frac{1}{x}\Big)</math>
+
*<math>\lim_{x\to\infty}x\sin\left(\tfrac{1}{x}\right)</math>
 +
'''פתרון''': נבצע הצבה <math>y=\frac{1}{x}</math> ולכן זה בעצם שווה לגבול
 +
:<math>\lim_{x\to\infty}x\sin\left(\tfrac{1}{x}\right)=\lim_{y\to 0^+}\frac{\sin(y)}{y}=1</math>
  
  
−
'''פתרון''':
+
*<math>\lim_{x\to 0}x\sin\left(\tfrac{1}{x}\right)</math>
−
 
+
'''פתרון''': שואפת לאפס כפול חסומה, לכן הגבול הנו <math>0</math> .
−
נבצע הצבה <math>y=\frac{1}{x}</math> ולכן זה בעצם שווה לגבול
+
−
 
+
−
::<math>\lim_{x\rightarrow \infty}xsin\Big(\frac{1}{x}\Big)=\lim_{y\rightarrow 0^+}\frac{1}{y}sin(y) = 1</math>
+
−
 
+
−
 
+
−
*<math>\lim_{x\rightarrow 0}xsin\Big(\frac{1}{x}\Big)</math>
+
−
 
+
−
'''פתרון''':
+
−
 
+
−
שואפת לאפס כפול חסומה, לכן הגבול הינו אפס
+
  
  
−
*<math>f(x)=\begin{cases}x^2 & x\in\mathbb{Q}\\ 0 & x\notin\mathbb{Q}\end{cases}</math>
+
*<math>f(x)=\begin{cases}x^2 & x\in\Q \\ 0 & x\notin\Q\end{cases}</math>
  
−
הראנו בסרטון על הגדרת הגבול לפי סדרות (לעיל) כי גבול פונקציה זו קיים אך ורק בנקודה אפס וערכו שם הוא אפס
+
הראנו בסרטון על הגדרת הגבול לפי סדרות (לעיל) כי גבול פונקציה זו קיים אך ורק בנקודה <math>0</math> וערכו שם הוא <math>0</math> .

גרסה אחרונה מ־01:35, 16 ביוני 2017

חזרה לפונקציות

כאשר למדנו גבולות של סדרות, היה רק כיוון אחד להתקדמות הסדרה - האינדקס שאף לאינסוף דרך הטבעיים. כאשר מדובר על פונקציה, x יכול לשאוף לכל מספר ממשי וגם לפלוס ומינוס אינסוף. בנוסף הוא עשוי לשאוף אליהם דרך מספרים רציונאליים, אי רציונאליים או גם וגם. עלינו להתאים את הגדרת הגבול של פונקציה בהתאם.

גבול פונקציה לפי קושי

הגדרה.

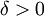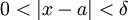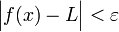L נקרא הגבול של f בנקודה a אם f מוגדרת בסביבה מנוקבת של a וגם לכל \varepsilon>0 קיים \delta>0 כך שלכל 0<|x-a|<\delta מתקיים \Big|f(x)-L\Big|<\varepsilon .

(הערה: סביבה מנוקבת של a הנה סביבה של a שמוציאים ממנה את a .)

הסבר ההגדרה: לכל מרחק על ציר y שנבחר (אפסילון) יש מרחק על ציר x (דלתא) כך שאם הנקודות על ציר x קרובות מספיק ל-a אזי הפונקציה עליהן קרובה מספיק ל-L .


תרגיל.

הוכח לפי ההגדרה כי 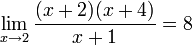\lim\limits_{x\to2}\dfrac{(x+2)(x+4)}{x+1}=8

פתרון

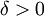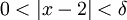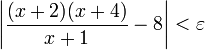
יהי \varepsilon>0 . צריך להוכיח כי קיים \delta>0 , כך שאם 0<|x-2|<\delta אזי מתקיים \left|\dfrac{(x+2)(x+4)}{x+1}-8\right|<\varepsilon

נפתח את הביטוי:

\left|\frac{(x+2)(x+4)}{x+1}-8\right|=\left|\frac{x^2+6x+8-8x-8}{x+1}\right|=\left|\frac{x^2-2x}{x+1}\right|=\left|\frac{x(x-2)}{x+1}\right|

אנו רואים כי כאשר 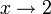x\to2 המונה שואף ל-0 והמכנה ל-3. נרצה, אם כך, לחסום את המכנה מלמטה על-ידי קבוע גדול מ-0, כך נוכל להקטין את המכנה, ולהגדיל את הביטוי.

כאשר 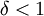\delta<1 , עבור 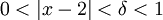0<|x-2|<\delta<1 מתקיים 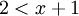2<x+1 ולכן:

\left|\dfrac{x(x-2)}{x+1}\right|<\dfrac{|x(x-2)|}{2}

כמו כן, מתקיים 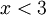x<3 ולכן:

\left|\dfrac{x(x-2)}{x+1}\right|<\dfrac{3|x-2|}{2}<\dfrac32\delta

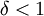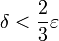לסיכום, קיים דלתא כך ש- \delta<1 וגם \delta<\dfrac23\varepsilon עבורו מתקיים:

\left|\dfrac{(x+2)(x+4)}{x+1}-8\right|<\dfrac32\delta=\varepsilon

גבול פונקציה לפי היינה

בהגדרת קושי לגבול פונקציה הכללנו את הרעיון של גבול של סדרה, אך לא השתמשנו בו. בהגדרת הגבול לפי היינה נסתמך על הגדרת הגבול של סדרה.

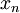הגדרה. L נקרא הגבול של f בנקודה a אם f מוגדרת בסביבה מנוקבת של a וגם לכל סדרה x_n המקיימת את שני התנאים הבאים:

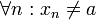
  • \forall n:x_n\ne a
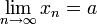  • \lim_{n\to\infty}x_n=a (כאשר זהו גבול של סדרות)

מתקיים כי הסדרה 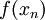f(x_n) שואפת ל- L (שוב, גבול של סדרות).

תרגיל.

הוכח כי 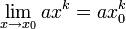\lim\limits_{x\to x_0}ax^k=ax_0^k

פתרון. לכל סדרה 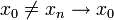x_0\ne x_n\to x_0 מתקיים לפי אריתמטיקת גבולות של סדרות כי

ax^k=a\cdot x\cdots x\to a\cdot x_0\cdots x_0=ax_0^k

מסקנה. קל להראות כי לכל פולינום p מתקיים 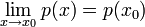\lim\limits_{x\to x_0}p(x)=p(x_0)

תרגיל.

הוכח כי לא קיים הגבול 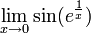\lim\limits_{x\to 0}\sin(e^{\frac{1}{x}})

הוכחה. נראה כי קיימות סדרות

0\ne x_k,y_k\to 0

כך ש-

\lim f(x_k)\ne\lim f(y_k)

נזכר בעובדה שלכל מספר שלם k מתקיים:

\sin\left(\frac{\pi}{2}+2\pi k\right)=1
\sin\left(\frac{3\pi}{2}+2\pi k\right)=-1

נרצה סדרה המקיימת

e^\frac{1}{x_k}=\frac{\pi}{2}+2\pi k

ולכן ניקח

x_k=\frac{1}{\ln\Big(\frac{\pi}{2}+2\pi k\Big)}

באופן דומה ניקח

y_k=\frac{1}{\ln\Big(\frac{3\pi}{2}+2\pi k\Big)}

ואז נקבל

\lim f(x_k)=1\ne -1=\lim f(y_k)

גבולות ידועים

\lim_{x\to 0}\frac{\sin(x)}{x}=1
\lim_{x\to 0}\frac{1-\cos(x)}{x}=0
\lim_{x\to 0}\frac{1-\cos(x)}{x^2}=\frac{1}{2}
\lim_{x\to 0}\frac{\ln(1+x)}{x}=1

דוגמאות

חשב את הגבולות הבאים:

  • \lim_{x\to 0}\frac{1-\cos(x)}{\sin(x)}

פתרון:

\lim_{x\to 0}\frac{1-\cos(x)}{\sin(x)}=\lim_{x\to 0}\frac{1-\cos(x)}{\sin(x)}\cdot\frac{x}{x}=\lim_{x\to 0}\frac{1-\cos(x)}{x}\frac{x}{\sin(x)}=0\cdot 1=0


  • \lim_{x\to 0}\frac{5x^2+2x}{3x^3+2x^2+x}

פתרון:

\lim_{x\to 0}\frac{5x^2+2x}{3x^3+2x^2+x}=\lim_{x\to 0}\frac{x(5x+2)}{x(3x^2+2x+1)}=\lim_{x\to 0}\frac{5x+2}{3x^2+2x+1}=2

הערה: שימו לב שכאשר המשתנה שואף לאפס, החזקה המשמעותית היא דווקא הנמוכה בניגוד לכאשר המשתנה שואף לאינסוף.


  • \lim_{x\to\infty}x\sin\left(\tfrac{1}{x}\right)

פתרון: נבצע הצבה 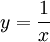y=\frac{1}{x} ולכן זה בעצם שווה לגבול

\lim_{x\to\infty}x\sin\left(\tfrac{1}{x}\right)=\lim_{y\to 0^+}\frac{\sin(y)}{y}=1


  • \lim_{x\to 0}x\sin\left(\tfrac{1}{x}\right)

פתרון: שואפת לאפס כפול חסומה, לכן הגבול הנו 0 .


  • f(x)=\begin{cases}x^2 & x\in\Q \\ 0 & x\notin\Q\end{cases}

הראנו בסרטון על הגדרת הגבול לפי סדרות (לעיל) כי גבול פונקציה זו קיים אך ורק בנקודה 0 וערכו שם הוא 0 .

מקור: https://math-wiki.com/index.php?title=גבול_פונקציה&oldid=71853