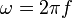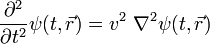הבדלים בין גרסאות בדף "גלים עומדים במיתר"

גרסה מ־13:01, 11 בפברואר 2015

גל הינו תופעה נפוצה המתארת הפרעה המתפשטת במרחב. גלים קיימים ונחקרים בתחומים שונים בפיזיקה למשל, גלים אלקטרומגנטיים, גלי קול, גלי מים ועוד. במעבדה זו נחקור גלים עומדים במיתר, תופעה זו מתקבל מתוך תכונותיו הבסיסיות של הגל ההרמוני. במהלך הניסוי יומחש המושג "גלים עומדים" בעזרת צפייה בגלים במיתר, מדידה של נקודות הצומת וחישוב מהירות הגל.

רקע תיאורטי

באוויר, במוצק ובנוזל נוצרים גלים מכניים הודות לכוחות אלסטיים, היוצרים קשרים בין חלקי גוף שונים. בתהליך יצירת גלים בתווך מסויים כמו מים או מיתר משתתפים כוחות כבידה וכוחות מתיחות.

גל במיתר ניתן לתיאור כמו כל גל אחר בעזרת משוואת גלים:

 $\ \frac{\partial^2 }{\partial t^2} \psi(t,\vec{r}) = v^2 \ \nabla ^2 \psi(t,\vec{r})$

זוהי משוואה דיפרנציאלית , שבה:

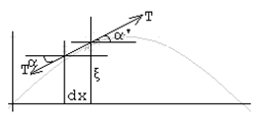
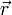$\vec{r}$ הוא המקום במרחב.
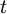$\ t$ הוא הזמן.
הפונקציה 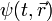$\ \psi (t,\vec{r})$ היא פונקציית הגל, המתארת מהי משרעת הגל בכל נקודה ובכל זמן.
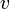$\ v$ היא מהירות התקדמות הגל.
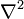$\ \nabla ^2$ הוא האופרטור לפלסיאן.

נחקור מיתר המתנודד ונקבל את משוואת הגלים עבורו בחד מימד.

איור 1 - סכמת כוחות על מיתר מתנודד

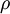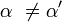נתון מיתר גמיש וגל עובר בו. נניח כי אמפליטודת הגל קטנה, הצפיפות $\rho$ , אורך המיתר $L$ והמתיחות $T$ (בשווי משקל). כעת נעוות את המיתר וניצור בו הפרעה, ראו איור 1. העיוות יהיה קטן כדי לא לשנות את המתיחות. נבחר קטע על המיתר ונתייחס רק אליו. קבענו כתנאי קודם שהמתיחות בשני הקצוות שווה והיא T. מתיחויות אלו אינן פועלות בכיוונים מנוגדים אלא בסטייה קטנה ( $\alpha\ \ne\alpha^\prime$ ), ולכן נוכל לכתוב משוואה לסכום הכוחות על הקטע שלנו:

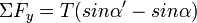
$\Sigma F_y=T(sin \alpha^\prime -sin \alpha)$

כיוון שמדובר בזוויות קטנות נחליף sin ב- tan ונקבל:

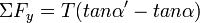$\Sigma F_y=T(tan \alpha^\prime -tan \alpha)$ .

זהו הפרש של tan, לכן נכתוב את המשוואה:

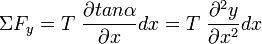
$\Sigma F_y=T\ \frac{\partial tan \alpha}{\partial x} dx=T\ \frac{\partial^2 y}{\partial x^2} dx$

כעת, נכתוב את החוק השני של ניוטון עבור מיתר זה:

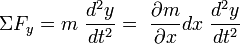
$\Sigma F_y=m\ \frac{d^2 y}{dt^2}=\ \frac{\partial m}{\partial x} dx \ \frac{d^2 y}{dt^2}$

נשווה בין שני התיאורים, ונקבל את משוואת הגלים:

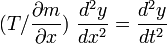
$(T/\frac{\partial m}{\partial x} )\ \frac{d^2 y}{dx^2}= \frac{d^2 y}{dt^2}$

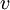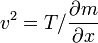
כאשר המהירות $v$ נתונה על ידי: $v^2=T/\frac{\partial m}{\partial x}$

גלים עומדים

כאשר מיתר מתנודד באופן מחזורי, והגל שנוצר מגיע למכשול מתבצעת החזרה מלאה. במקרה זה, נקבל במיתר שני גלים זהים זה לזה בתדירות ובמשרעת והפוכים בכיוון התקדמותם. ההעתק של כל נקודה במיתר במקרה זה יהיה שווה לסכום האלגברי של ההעתקים של שני הגלים. התוצאה של הסופרפוזיציה, במקרה זה, היא אופן תנודה בעל תכונות מיוחדות, המכונה גל עומד. נכתוב את משוואת הגל עבור הסופרפוזיציה:

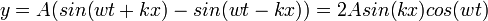
$y=A(sin(wt+kx)-sin(wt-kx))=2Asin(kx)cos(wt)$

זוהי תנועה הרמונית פשוטה באמפליטודה משתנה, שערכה: 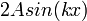$2Asin(kx)$ . בנקודות מסוימות במיתר האמפליטודה מתאפסת בכל זמן. נקודות אלו נקראות nodes, ומיקומם תלוי באורך הגל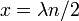 $x=\lambda n/2$

כאשר מדובר על הפרעה מחזורית אנו מגדירים מאפיינים לתיאורו של הגל:

$f$ , תדירות הגל - מספר המחזורים בשנייה, נמדדת ביחידות של הרץ ( $Hz$ ).

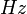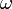$\omega$ , תדירות זוויתית - נירמול תדירות הגל כך ש- $\omega = 2 \pi f$

גרסה מ־12:50, 11 בפברואר 2015 (הצגת מקור) נועה ק (שיחה \| תרומות) (←‏גלים עומדים) → מעבר להשוואת הגרסאות הקודמת		גרסה מ־13:01, 11 בפברואר 2015 (הצגת מקור) נועה ק (שיחה \| תרומות) (←‏גלים עומדים) מעבר להשוואת הגרסאות הבאה ←
שורה 52:		שורה 52:
	<math>y=A(sin(wt+kx)-sin(wt-kx))=2Asin(kx)cos(wt)</math>		<math>y=A(sin(wt+kx)-sin(wt-kx))=2Asin(kx)cos(wt)</math>

−	זוהי תנועה הרמונית פשוטה באמפליטודה משתנה, שערכה: <math>2Asin(kx)</math>.	+	זוהי תנועה הרמונית פשוטה באמפליטודה משתנה, שערכה: <math>2Asin(kx)</math>. בנקודות מסוימות במיתר האמפליטודה מתאפסת בכל זמן. נקודות אלו נקראות nodes, ומיקומם תלוי באורך הגל <math>x=\lambda n/2</math>

הבדלים בין גרסאות בדף "גלים עומדים במיתר"

גרסה מ־13:01, 11 בפברואר 2015

רקע תיאורטי

גלים עומדים

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים