הבדלים בין גרסאות בדף "דוגמאות להוכחת התכנסות באמצעות קריטריון קושי"
מתוך Math-Wiki
(דף חדש: ==תיקון טעות מהתרגיל של יום ראשון== '''תרגיל''': תהי סדרה <math>\{a_n\}</math> כך ש <math>|a_n-a_{n-1}|<\frac{1}{2^n}</math>. הוכח ש<math>\…) |
(←תיקון טעות מהתרגיל של יום ראשון) |
||
| שורה 1: | שורה 1: | ||
| − | == | + | ===תרגיל 1=== |
'''תרגיל''': תהי סדרה <math>\{a_n\}</math> כך ש <math>|a_n-a_{n-1}|<\frac{1}{2^n}</math>. הוכח ש<math>\{a_n\}</math> מתכנסת. | '''תרגיל''': תהי סדרה <math>\{a_n\}</math> כך ש <math>|a_n-a_{n-1}|<\frac{1}{2^n}</math>. הוכח ש<math>\{a_n\}</math> מתכנסת. | ||
| שורה 12: | שורה 12: | ||
<math>=\frac{1}{2^{n+1}}[\frac{1-\frac{1}{2^{m-n}}}{1-\frac{1}{2}}]=\frac{1}{2^n}[1-\frac{1}{2^{m-n}}]=\frac{1}{2^n}-\frac{1}{2^m}\leq \frac{1}{2^n} \rightarrow 0</math> | <math>=\frac{1}{2^{n+1}}[\frac{1-\frac{1}{2^{m-n}}}{1-\frac{1}{2}}]=\frac{1}{2^n}[1-\frac{1}{2^{m-n}}]=\frac{1}{2^n}-\frac{1}{2^m}\leq \frac{1}{2^n} \rightarrow 0</math> | ||
| + | |||
| + | |||
| + | ===תרגיל 2=== | ||
| + | '''תרגיל''': תהי סדרה <math>\{a_n\}</math> כך ש <math>|a_{n+1}-a_n|\leq p|a_n-a_{n-1}|</math>, עבור <math>0<p<1</math> הוכח ש<math>\{a_n\}</math> מתכנסת. | ||
| + | |||
| + | '''פתרון''': נוכיח ש <math>\{a_n\}</math> סדרת קושי, ולכן מתכנסת. | ||
| + | |||
| + | דבר ראשון, נשים לב ש- <math>|a_{n+1}-a_n|\leq p|a_n-a_{n-1}|\leq p^2|a_{n-1}-a_{n-2}|\leq ...\leq p^{n-1}|a_2-a_1|</math>. נסמן <math>d=|a_2-a_1|</math> ולכן סה"כ <math>|a_{n+1}-a_n|\leq p^{n-1}d</math> | ||
| + | |||
| + | |||
| + | |||
| + | כעת, | ||
| + | |||
| + | <math>|a_m-a_n|=|a_m-a_{m-1}+a_{m-1}-a_{m-2}+...-a_{n+1}+a_{n+1}-a_n|\leq </math> | ||
| + | |||
| + | <math>\leq |a_m-a_{m-1}|+|a_{m-1}-a_{m-2}|+...+|a_{n+1}-a_n|\leq</math> | ||
| + | |||
| + | <math>\leq p^{m-2}d+...+p^{n-1}d = p^{n-1}d(p^{m-n-1}+...+1)=p^{n-1}d(\frac{1-p^{m-n-1}}{1-p}) \leq p^{n-1}\frac{d}{1-p} \rightarrow 0 </math> (לפי מה שהראנו) | ||
| + | |||
| + | מכיוון ש<math>p^n\rightarrow 0</math> עבור p<1. | ||
גרסה מ־12:34, 8 בנובמבר 2010
תרגיל 1
תרגיל: תהי סדרה 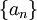 כך ש
כך ש 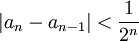 . הוכח ש
. הוכח ש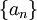 מתכנסת.
מתכנסת.
פתרון: נוכיח ש 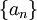 סדרת קושי, ולכן מתכנסת.
סדרת קושי, ולכן מתכנסת.
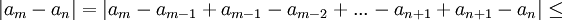
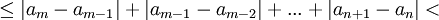
![< \frac{1}{2^m}+\frac{1}{2^{m-1}}+...+\frac{1}{2^{n+1}}=\frac{1}{2^{n+1}}[\frac{1}{2^{m-n-1}}+...+1]](/images/math/6/3/f/63f1941dac32cf4a806aa8099d41e4a0.png) (לפי הנתון)
(לפי הנתון)
![=\frac{1}{2^{n+1}}[\frac{1-\frac{1}{2^{m-n}}}{1-\frac{1}{2}}]=\frac{1}{2^n}[1-\frac{1}{2^{m-n}}]=\frac{1}{2^n}-\frac{1}{2^m}\leq \frac{1}{2^n} \rightarrow 0](/images/math/c/4/6/c46caed05fe1571e189d2e8877d27c21.png)
תרגיל 2
תרגיל: תהי סדרה 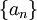 כך ש
כך ש 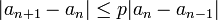 , עבור
, עבור 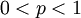 הוכח ש
הוכח ש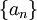 מתכנסת.
מתכנסת.
פתרון: נוכיח ש 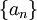 סדרת קושי, ולכן מתכנסת.
סדרת קושי, ולכן מתכנסת.
דבר ראשון, נשים לב ש- 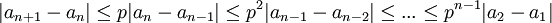 . נסמן
. נסמן 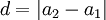 ולכן סה"כ
ולכן סה"כ 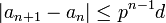
כעת,
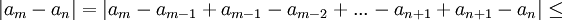
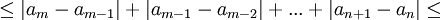
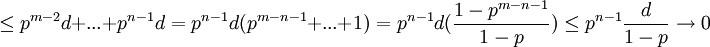 (לפי מה שהראנו)
(לפי מה שהראנו)
מכיוון ש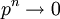 עבור p<1.
עבור p<1.