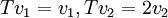דמיון בין מטריצות
מתוך Math-Wiki
הגדרה
נביט בקבוצה כל המטריצות הריבועיות מסדר n ונגדיר את יחס הדמיון בין מטריצות על ידי:
- A דומה ל B אם קיימת מטריצה הפיכה P כך ש
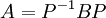
שימוש בדמיון לחקר העתקות לינארית
- ראשית, קל להראות כי יחס הדמיון הינו יחס שקילות
- שנית, ניזכר כי כל מטריצה הפיכה מהווה מטריצת מעבר בין בסיסים
- שלישית נזכר בנוסחא להעברת בסיסים של מטריצה המייצגת העתקה
משלושת אלה יחדיו נסיק כי:
- מטריצות הינן דומות זו לזו אם"ם הן מייצגות את אותה העתקה לינארית לפי בסיסים כלשהם
לכן על מנת לחקור העתקות לינאריות נמצא מטריצה "יפה" הדומה למטריצה המייצגת את ההעתקה.
דוגמא
נבחן את המטריצה
מטריצה זו מייצגת את ההעתקה הלינארית הבאה:
לאחר מציאת ערכים עצמיים והפעלת אלגוריתם ללכסון מטריצה נקבל כי המטריצה המייצגת את T הינה
כאשר 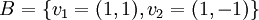
לכן לפי התכונות של מטריצה מייצגת מתקיים
במילים פיזיקליות, ההעתקה מכפילה את הכוח בכיוון 135 מעלות.
הערה:
אמנם לא כל העתקה ניתן להביא לצורה יפה כזו, אך כאשר נלמד את משפט ז'ורדן נאפיין בדיוק את כל ההעתקות הלינאריות מעל המרוכבים לפי צורות הז'ורדן שלהן.
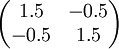
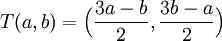
![[T]_B=\begin{pmatrix} 1 & 0 \\ 0 & 2\end{pmatrix}](/images/math/8/e/d/8ed5a1ac62e131aa1e0e5534086699ef.png)