הבדלים בין גרסאות בדף "הלמה של קנטור"
מתוך Math-Wiki
מ (משפטים/אינפי/למת קנטור הועבר להלמה של קנטור) |
|||
| שורה 16: | שורה 16: | ||
לכן הנקודה c שייכת לכל הקטעים. נניח והייתה נקודה נוספת <math>c\neq d</math> השייכת לכל הקטעים. לכן אורך כל הקטעים הוא לפחות <math>|d-c|>0</math> בסתירה לכך שהאורך שואף לאפס. | לכן הנקודה c שייכת לכל הקטעים. נניח והייתה נקודה נוספת <math>c\neq d</math> השייכת לכל הקטעים. לכן אורך כל הקטעים הוא לפחות <math>|d-c|>0</math> בסתירה לכך שהאורך שואף לאפס. | ||
| + | |||
| + | [[קטגוריה:אינפי]] | ||
גרסה מ־00:56, 15 בפברואר 2012
הלמה של קנטור
תהי 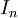 סדרה של קטעים סגורים המוכלים זה בזה
סדרה של קטעים סגורים המוכלים זה בזה 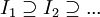 , כך שאורך הקטעים שואף לאפס. אזי קיימת נקודה יחידה c הנמצאת בכל הקטעים.
, כך שאורך הקטעים שואף לאפס. אזי קיימת נקודה יחידה c הנמצאת בכל הקטעים.
הוכחה
נסמן ![I_n=[a_n,b_n]](/images/math/8/9/6/896f17899a5f55ed35de918753570d00.png) . לפי הנתון שהקטעים מוכלים זה בזה, ניתן להסיק כי
. לפי הנתון שהקטעים מוכלים זה בזה, ניתן להסיק כי  מונוטונית עולה וחסומה על ידי
מונוטונית עולה וחסומה על ידי 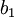 , ואילו
, ואילו  מונוטונית יורדת וחסומה על ידי
מונוטונית יורדת וחסומה על ידי 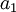 .
.
לכן שתי הסדרות מונוטוניות וחסומות ולכן מתכנסות. כיוון שאורך הקטעים שואף לאפס, 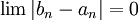 ולכן גבול הסדרות זהה. נוכיח כי הנקודה
ולכן גבול הסדרות זהה. נוכיח כי הנקודה
מקיימת את הדרוש.
נניח בשלילה, כי קיים קטע כך ש ![c\notin [a_k,b_k]](/images/math/3/7/0/3706275ae8c0a2831c8d43f6d41dfb5c.png) . לכן
. לכן 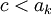 או
או 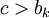 וכיוון שאילו סדרות מונוטוניות, הגבול שלהן שונה מ-c בסתירה. (
וכיוון שאילו סדרות מונוטוניות, הגבול שלהן שונה מ-c בסתירה. (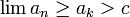 או
או 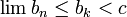 .)
.)
לכן הנקודה c שייכת לכל הקטעים. נניח והייתה נקודה נוספת 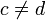 השייכת לכל הקטעים. לכן אורך כל הקטעים הוא לפחות
השייכת לכל הקטעים. לכן אורך כל הקטעים הוא לפחות 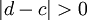 בסתירה לכך שהאורך שואף לאפס.
בסתירה לכך שהאורך שואף לאפס.