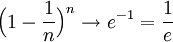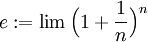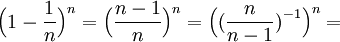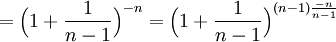הבדלים בין גרסאות בדף "המספר e"
מתוך Math-Wiki
(יצירת דף עם התוכן "חזרה לסדרות ==המספר e== הוכחנו בהרצאה כי לסדרה <m...") |
(←המספר e) |
||
| שורה 10: | שורה 10: | ||
'''משפט.''' תהי <math>a_n</math> סדרה כלשהי המתכנסת במובן הרחב לאינסוף, ותהי <math>b_n</math> סדרה המתכנסת (במובן הצר, או במובן הרחב) לגבול L. אזי <math>e^L=\lim\Big(1+\frac{1}{a_n}\Big)^{a_n\cdot b_n}</math> | '''משפט.''' תהי <math>a_n</math> סדרה כלשהי המתכנסת במובן הרחב לאינסוף, ותהי <math>b_n</math> סדרה המתכנסת (במובן הצר, או במובן הרחב) לגבול L. אזי <math>e^L=\lim\Big(1+\frac{1}{a_n}\Big)^{a_n\cdot b_n}</math> | ||
| + | |||
| + | |||
| + | <font size=4 color=#a7adcd> | ||
| + | '''תרגיל.''' | ||
| + | </font> | ||
| + | |||
| + | חשב את גבול הסדרה <math>a_n=\Big(1-\frac{1}{n}\Big)^n</math> | ||
| + | |||
| + | |||
| + | '''פתרון.''' נפתח את הסדרה על מנת לקבל ביטוי מהצורה של המשפט למעלה. | ||
| + | |||
| + | |||
| + | ::<math>\Big(1-\frac{1}{n}\Big)^n=\Big(\frac{n-1}{n}\Big)^n=\Big(\big(\frac{n}{n-1}\big)^{-1}\Big)^n=</math> | ||
| + | |||
| + | |||
| + | ::<math>=\Big(1+\frac{1}{n-1}\Big)^{-n}=\Big(1+\frac{1}{n-1}\Big)^{(n-1)\frac{-n}{n-1}}</math> | ||
| + | |||
| + | |||
| + | כיוון ש <math>\frac{-n}{n-1}\rightarrow (-1)</math> אנו מקבלים כי | ||
| + | |||
| + | <math>\Big(1-\frac{1}{n}\Big)^n\rightarrow e^{-1}=\frac{1}{e}</math> | ||
גרסה מ־09:41, 21 בדצמבר 2011
המספר e
הוכחנו בהרצאה כי לסדרה 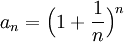 יש גבול ממשי. אנו מגדירים את המספר e להיות גבול הסדרה הזו.
יש גבול ממשי. אנו מגדירים את המספר e להיות גבול הסדרה הזו.
משפט. תהי  סדרה כלשהי המתכנסת במובן הרחב לאינסוף, אזי
סדרה כלשהי המתכנסת במובן הרחב לאינסוף, אזי 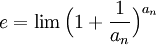
משפט. תהי  סדרה כלשהי המתכנסת במובן הרחב לאינסוף, ותהי
סדרה כלשהי המתכנסת במובן הרחב לאינסוף, ותהי  סדרה המתכנסת (במובן הצר, או במובן הרחב) לגבול L. אזי
סדרה המתכנסת (במובן הצר, או במובן הרחב) לגבול L. אזי 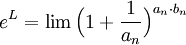
תרגיל.
חשב את גבול הסדרה 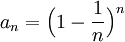
פתרון. נפתח את הסדרה על מנת לקבל ביטוי מהצורה של המשפט למעלה.
כיוון ש 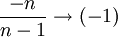 אנו מקבלים כי
אנו מקבלים כי