הבדלים בין גרסאות בדף "המשפט היסודי של החדוא"

גרסה מ־22:08, 7 בפברואר 2017

המשפט היסודי של החדו"א

המשפט היסודי של החדו"א, או משפט ניוטון-לייבניץ, נותן דרך לחישוב האינטגרל המסוים, ולמעשה, מראה את הקשר ההדוק הקיים בין האינטגרל המסוים לבין האינטגרל הלא-מסוים.

הניסוח:

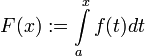תהי $f$ פונקציה אינטגרבילית על הקטע $[a,b]$ , ונגדיר $F(x):=\int\limits_a^xf(t)dt$ . אזי:

הפונקציה $F$ רציפה.
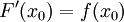בכל נקודה $x_0$ שבה $f$ רציפה, $F$ גזירה, וכן $F'(x_0)=f(x_0)$ .

מסקנה מהמשפט היא שאם $f$ רציפה, הפונקציה $F$ שהגדרנו היא פונקציה קדומה שלה (ובפרט, יש ל- $f$ פונקציה קדומה).

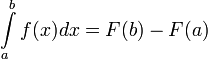אם הפונקציה $f$ רציפה, מקבלים את נוסחת ניוטון-לייבניץ: אם $F$ פונקציה קדומה של $f$ , אזי $\displaystyle\int\limits_a^b f(x)dx=F(b)-F(a)$ .

@@ שורה 5: / שורה 5: @@
 הניסוח:
-תהי <math>f</math> פונקציה אינטגרבילית על הקטע <math>[a,b]</math>, ונגדיר <math>F(x):=\int\limits_a^x {f(t)dt}</math>. אזי:
+תהי <math>f</math> פונקציה אינטגרבילית על הקטע <math>[a,b]</math> , ונגדיר <math>F(x):=\int\limits_a^xf(t)dt</math> . אזי:
 *הפונקציה <math>F</math> רציפה.
-*בכל נקודה <math>x_0</math> שבה <math>f</math> רציפה, <math>F</math> גזירה, וכן <math>F'(x_0)=f(x_0)</math>.
+*בכל נקודה <math>x_0</math> שבה <math>f</math> רציפה, <math>F</math> גזירה, וכן <math>F'(x_0)=f(x_0)</math> .
 מסקנה מהמשפט היא שאם <math>f</math> רציפה, הפונקציה <math>F</math> שהגדרנו היא פונקציה קדומה שלה (ובפרט, יש ל- <math>f</math> פונקציה קדומה).
 אם הפונקציה <math>f</math> רציפה, מקבלים את '''נוסחת ניוטון-לייבניץ''': אם <math>F</math> פונקציה קדומה של <math>f</math>, אזי <math>\displaystyle\int\limits_a^b f(x)dx=F(b)-F(a)</math> .

הבדלים בין גרסאות בדף "המשפט היסודי של החדוא"

גרסה מ־22:08, 7 בפברואר 2017

המשפט היסודי של החדו"א

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים