הבדלים בין גרסאות בדף "המשפט היסודי של החשבון האינטגרלי"
(←סעיף ב') |
יהודה שמחה (שיחה | תרומות) מ |
||
| שורה 1: | שורה 1: | ||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
| − | == המשפט == | + | ==המשפט== |
| − | תהי <math>f(x)</math> מוגדרת, חסומה ואינטגרבילית ב-<math>[a,b]</math>. נגדיר גם: <math>\forall x \in [a,b]: A(x):= \ | + | תהי <math>f(x)</math> מוגדרת, חסומה ואינטגרבילית ב-<math>[a,b]</math>. נגדיר גם: |
| + | <math>\forall x\in [a,b]: A(x):= \displaystyle\int\limits_a^x f(t)dt</math> . אזי מתקיים: | ||
א) <math>A(x)</math> רציפה. | א) <math>A(x)</math> רציפה. | ||
| − | ב)לכל <math> | + | ב) לכל <math>x_0\in [a,b]</math> שבו <math>f(x_0)</math> רציפה, <math>A(x)</math> גזירה ו- <math>A'(x_0)=f(x_0)</math>. |
| − | ג) אם <math>f(x)</math> רציפה בכל <math>[a,b]</math>, ו-F פונקציה קדומה של f, מתקיימת נוסחת ניוטון-לייבניץ: <math>\ | + | ג) אם <math>f(x)</math> רציפה בכל <math>[a,b]</math>, ו- <math>F</math> פונקציה קדומה של <math>f</math>, מתקיימת נוסחת ניוטון-לייבניץ: <math>\displaystyle\int\limits_a^b f(x)dx=F(b)-F(a)</math>. |
| − | == הוכחה == | + | ==הוכחה== |
=== סעיף א'=== | === סעיף א'=== | ||
| − | נקח <math>x \in [a,b]</math> כלשהו ו-<math>\Delta x</math> "קטן" כך ש-<math>x+\Delta x \in [a,b]</math>. לפי הגדרה:<math>A(x+\Delta x)=\ | + | נקח <math>x\in [a,b]</math> כלשהו ו- <math>\Delta x</math> "קטן" כך ש-<math>x+\Delta x\in [a,b]</math>. לפי הגדרה: <math>A(x+\Delta x)=\displaystyle\int\limits_a^{x+\Delta x}f(t)dt</math> ולכן |
| − | <math>A(x+\Delta x)-A(x)=\ | + | <math>A(x+\Delta x)-A(x)=\displaystyle\int\limits_x^{x+\Delta x} f(t)dt</math>. נתון ש- <math>f</math> חסומה, נגיד <math>f(x)\le M </math>. |
| − | נתון ש-f חסומה, נגיד <math>f(x) \ | + | |
| − | לכן מתקיים | + | לכן מתקיים <math>\bigg|A(x+\Delta x)-A(x)\bigg|=\Bigg|\displaystyle\int\limits_x^{x+\Delta x}f(t)dt\Bigg|\le M|\Delta x|</math>. |
כעת נשאיף את <math>\Delta x \to 0</math>, אגף ימין שואף ל-0 . | כעת נשאיף את <math>\Delta x \to 0</math>, אגף ימין שואף ל-0 . | ||
לכן: | לכן: | ||
| − | <math>\lim_{\Delta x \to 0}|A(x+\Delta x)-A(x)|=0</math> | + | <math>\lim_{\Delta x\to 0}\bigg|A(x+\Delta x)-A(x)\bigg|=0</math> ומכך נובע ש: |
| − | <math>\lim_{\Delta x \to 0}[A(x+\Delta x)-A(x)]=0</math> ולכן מתקיים תנאי הרציפות, | + | <math>\lim_{\Delta x\to 0}[A(x+\Delta x)-A(x)]=0</math> ולכן מתקיים תנאי הרציפות, |
| − | <math>\lim_{\Delta x \to 0}A(x+ \Delta x)= A(x)</math>. | + | <math>\lim_{\Delta x\to 0}A(x+\Delta x)=A(x)</math>. |
| − | <math>\blacksquare </math> | + | <math>\blacksquare</math> |
=== סעיף ב'=== | === סעיף ב'=== | ||
| − | כאן מניחים ש- <math>f(t)</math> רציפה בנקודה <math> | + | כאן מניחים ש- <math>f(t)</math> רציפה בנקודה <math>x_0\in [a,b]</math> כלשהי. אנחנו צריכים להוכיח כי <math>A'(x_0)</math> קיימת ושווה ל- <math>f(x_0)</math>. נחזור לפונקציה <math>A(x+\Delta x)-A(x)=\displaystyle\int\limits_x^{x+\Delta x}f(t)dt</math>. בעצם, אנחנו צריכים להוכיח כאן שכאשר <math>\Delta x\to 0</math> , מתקיים בהכרח: |
| − | בעצם, אנחנו צריכים להוכיח כאן שכאשר <math>\Delta x \to 0</math> , | + | |
| − | <math>\frac{A( | + | <math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}=\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x}f(t)dt \to f(x_0)</math> |
| − | '''טענה''' נוכיח כי | + | '''טענה:''' נוכיח כי <math>\lim\limits_{\Delta x\to 0}\Bigg[\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x}f(t)dt\Bigg]=f(x_0)</math> . |
| − | <math>\ | + | |
| − | נעיר קודם כל כי מתקיים ע"פ סעיף 6 במשפט 1: <math>\ | + | נעיר קודם כל כי מתקיים ע"פ סעיף 6 במשפט 1: <math>\int\limits_{x_0}^{x_0+\Delta x}f(x_0)dt=f(x_0) \Delta x</math> ולכן |
| − | + | <math>\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x} f(x_0)=f(x_0)</math>. | |
| − | כעת נראה כי הביטוי מתאפס: | + | כעת נראה כי הביטוי מתאפס: <math>\lim\limits_{\Delta x\to 0}\Bigg[\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x}[f(t)-f(x_0)]dt\Bigg]=0</math> |
| − | <math>\ | + | |
| − | יהי <math>\epsilon >0</math>. | + | יהי <math>\epsilon >0</math>. כיון ש- <math>f</math> רציפה, קיים <math>\delta >0</math> כך שאם <math>|t-x_0|< \delta</math> אז <math>\Big|f(t)-f(x_0)\Big|< \epsilon</math>. כעת נניח <math>|\Delta x|<\delta</math>, לכן לכל t כזה: <math>|t-x_0|\le |\Delta x|< \delta </math> כך ש-<math>\Big|f(t)-f(x_0)\Big|< \epsilon</math>. |
| − | מכאן ש- | + | מכאן ש- <math>\Bigg|\displaystyle\int\limits_{x_0}^{x_0+\Delta x}[f(t)-f(x_0)]dt\Bigg|\le \displaystyle\int\limits_{x_0}^{x_0+\Delta x}\Big|f(t)-f(x_0)\Big|dt< \displaystyle\int\limits_{x_0}^{x_0+\Delta x}\epsilon\cdot dt</math> |
| − | <math>|\ | + | |
| − | אבל <math>\ | + | אבל <math>\displaystyle\int\limits_{x_0}^{x_0+\Delta x}\epsilon\cdot dt=|\Delta x| \epsilon</math> ולכן |
| − | <math>|\ | + | <math>\Bigg|\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x}[f(t)-f(x_0)]dt\Bigg| < \frac1{|\Delta x|}\cdot \epsilon |\Delta x|=\epsilon </math>. |
| − | ולכן הגבול אכן שואף ל-0, מה שמעיד על כך שאגף ימין שואף ל-<math>f( | + | ולכן הגבול אכן שואף ל- <math>0</math>, מה שמעיד על כך שאגף ימין שואף ל- <math>f(x_0)</math>, ולכן, אגף שמאל גם שואף ל- <math>f(x_0)</math>, מכאן נובע <math>A'(x_0)=f(x_0)</math>. |
<math>\blacksquare</math> | <math>\blacksquare</math> | ||
===סעיף ג' === | ===סעיף ג' === | ||
| + | ידוע כי <math>f</math> רציפה על כל <math>[a,b]</math>, ולכן ע"פ סעיף ב', <math>A(x)</math> פונקציה קדומה של <math>f</math>. נתון גם כי <math>F</math> פונקציה קדומה של <math>f</math>, ולכן ע"פ המשפט הראשון של אינפי 2 מתקיים <math>F(x)=A(x)+C</math> עבור <math>C</math> כלשהו. | ||
| − | + | לכן: <math>F(b)-F(a)=[A(b)+C]-[A(a)+C]=A(b)-A(a)=\displaystyle\int\limits_a^b f(x)dx - \displaystyle\int\limits_a^a f(x)dx=</math> | |
| − | + | ||
| − | לכן: <math>F(b)-F(a)=[A(b)+ | + | |
| − | <math>=\ | + | <math>=\displaystyle\int\limits_a^b f(x)dx-0 = \displaystyle\int\limits_a^b f(x)dx</math> |
| − | ולכן בסך הכל :<math>\ | + | ולכן בסך הכל :<math>\displaystyle\int\limits_a^b f(x)dx=F(b)-F(a)</math>. |
<math>\blacksquare</math> | <math>\blacksquare</math> | ||
גרסה מ־18:13, 26 בינואר 2016
תוכן עניינים
המשפט
תהי  מוגדרת, חסומה ואינטגרבילית ב-
מוגדרת, חסומה ואינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נגדיר גם:
. נגדיר גם:
![\forall x\in [a,b]: A(x):= \displaystyle\int\limits_a^x f(t)dt](/images/math/1/0/3/103aee5cad38aa60cb97301915041159.png) . אזי מתקיים:
. אזי מתקיים:
א) 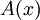 רציפה.
רציפה.
ב) לכל ![x_0\in [a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) שבו
שבו 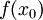 רציפה,
רציפה, 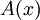 גזירה ו-
גזירה ו- 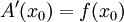 .
.
ג) אם  רציפה בכל
רציפה בכל ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ו-
, ו-  פונקציה קדומה של
פונקציה קדומה של  , מתקיימת נוסחת ניוטון-לייבניץ:
, מתקיימת נוסחת ניוטון-לייבניץ: 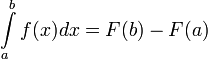 .
.
הוכחה
סעיף א'
נקח ![x\in [a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) כלשהו ו-
כלשהו ו- 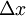 "קטן" כך ש-
"קטן" כך ש-![x+\Delta x\in [a,b]](/images/math/5/9/7/5975d5cd7e8bd0f64dfe5aa6a1877385.png) . לפי הגדרה:
. לפי הגדרה: 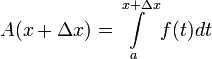 ולכן
ולכן
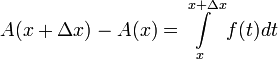 . נתון ש-
. נתון ש-  חסומה, נגיד
חסומה, נגיד 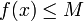 .
.
לכן מתקיים 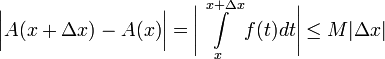 .
.
כעת נשאיף את 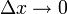 , אגף ימין שואף ל-0 .
לכן:
, אגף ימין שואף ל-0 .
לכן:
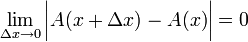 ומכך נובע ש:
ומכך נובע ש:
![\lim_{\Delta x\to 0}[A(x+\Delta x)-A(x)]=0](/images/math/1/3/7/1375310a0443665e243a8fd5c3c0c3c8.png) ולכן מתקיים תנאי הרציפות,
ולכן מתקיים תנאי הרציפות,
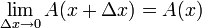 .
.

סעיף ב'
כאן מניחים ש- 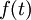 רציפה בנקודה
רציפה בנקודה ![x_0\in [a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) כלשהי. אנחנו צריכים להוכיח כי
כלשהי. אנחנו צריכים להוכיח כי 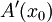 קיימת ושווה ל-
קיימת ושווה ל- 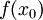 . נחזור לפונקציה
. נחזור לפונקציה 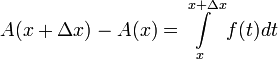 . בעצם, אנחנו צריכים להוכיח כאן שכאשר
. בעצם, אנחנו צריכים להוכיח כאן שכאשר 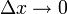 , מתקיים בהכרח:
, מתקיים בהכרח:
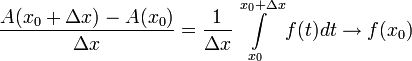
טענה: נוכיח כי ![\lim\limits_{\Delta x\to 0}\Bigg[\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x}f(t)dt\Bigg]=f(x_0)](/images/math/6/5/2/652ccf963d0a46dcb69bcd36568091f9.png) .
.
נעיר קודם כל כי מתקיים ע"פ סעיף 6 במשפט 1: 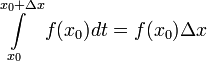 ולכן
ולכן
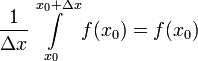 .
.
כעת נראה כי הביטוי מתאפס: ![\lim\limits_{\Delta x\to 0}\Bigg[\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x}[f(t)-f(x_0)]dt\Bigg]=0](/images/math/7/c/c/7cc55586af8dac3c5a068f3ba60014cf.png)
יהי 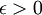 . כיון ש-
. כיון ש-  רציפה, קיים
רציפה, קיים 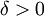 כך שאם
כך שאם 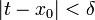 אז
אז 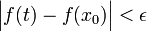 . כעת נניח
. כעת נניח 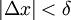 , לכן לכל t כזה:
, לכן לכל t כזה: 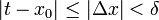 כך ש-
כך ש-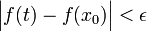 .
.
מכאן ש- ![\Bigg|\displaystyle\int\limits_{x_0}^{x_0+\Delta x}[f(t)-f(x_0)]dt\Bigg|\le \displaystyle\int\limits_{x_0}^{x_0+\Delta x}\Big|f(t)-f(x_0)\Big|dt< \displaystyle\int\limits_{x_0}^{x_0+\Delta x}\epsilon\cdot dt](/images/math/4/3/9/4393ef324c1fa3ac0f0cc5837846868e.png)
אבל 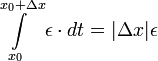 ולכן
ולכן
![\Bigg|\frac1{\Delta x}\displaystyle\int\limits_{x_0}^{x_0+\Delta x}[f(t)-f(x_0)]dt\Bigg| < \frac1{|\Delta x|}\cdot \epsilon |\Delta x|=\epsilon](/images/math/a/1/7/a174699e45a4e544edc38ee701d92dd0.png) .
.
ולכן הגבול אכן שואף ל-  , מה שמעיד על כך שאגף ימין שואף ל-
, מה שמעיד על כך שאגף ימין שואף ל- 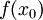 , ולכן, אגף שמאל גם שואף ל-
, ולכן, אגף שמאל גם שואף ל- 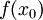 , מכאן נובע
, מכאן נובע 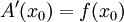 .
.

סעיף ג'
ידוע כי  רציפה על כל
רציפה על כל ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ולכן ע"פ סעיף ב',
, ולכן ע"פ סעיף ב', 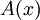 פונקציה קדומה של
פונקציה קדומה של  . נתון גם כי
. נתון גם כי  פונקציה קדומה של
פונקציה קדומה של  , ולכן ע"פ המשפט הראשון של אינפי 2 מתקיים
, ולכן ע"פ המשפט הראשון של אינפי 2 מתקיים 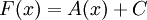 עבור
עבור 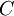 כלשהו.
כלשהו.
לכן: ![F(b)-F(a)=[A(b)+C]-[A(a)+C]=A(b)-A(a)=\displaystyle\int\limits_a^b f(x)dx - \displaystyle\int\limits_a^a f(x)dx=](/images/math/1/6/2/162493dd126cf592a369788258504093.png)
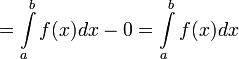
ולכן בסך הכל :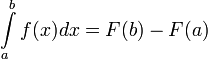 .
.
