הבדלים בין גרסאות בדף "התאמת גלואה"
יהודה שמחה (שיחה | תרומות) |
|||
| שורה 1: | שורה 1: | ||
התאמת גלואה היא הלב של תורת גלואה ועליה מושתתות הרבה תוצאות חשובות. ההתאמה מתבטאת במשפט היסודי של תורת גלואה הקובע כי יש התאמה בין שדות ביניים של הרחבת גלואה ובין תתי החבורות של חבורת גלואה שלה. | התאמת גלואה היא הלב של תורת גלואה ועליה מושתתות הרבה תוצאות חשובות. ההתאמה מתבטאת במשפט היסודי של תורת גלואה הקובע כי יש התאמה בין שדות ביניים של הרחבת גלואה ובין תתי החבורות של חבורת גלואה שלה. | ||
| − | + | ==המשפט היסודי של תורת גלואה== | |
| − | == המשפט היסודי של תורת גלואה == | + | '''משפט:''' תהי <math>E/F</math> הרחבת גלואה מממד סופי ותהי <math>G=\text{Gal}(E/F)</math> אזי קיימת התאמה חח"ע ועל בין: |
| − | + | :א. תת־שדות <math>F\sube K\sube E</math> | |
| − | '''משפט:''' תהי <math>E/F</math> הרחבת גלואה | + | :ב. תת־חבורות <math>H\le G</math> |
| − | :א. | + | ההתאמה שולחת חבורה <math>H</math> אל השדה <math>E^H=\bigl\{a\in E:\sigma a=a~\forall\sigma\in H\bigr\}</math> ותת־שדה <math>F\sube K\sube E</math> אל החבורה <math>\text{Gal}(E/K)</math> (פונקציות אלו הפוכות זו לזו). בנוסף, ההתאמה מקיימת: |
| − | :ב. | + | |
| − | ההתאמה שולחת חבורה <math>H</math> אל השדה <math>E^H=\{a\in E | + | |
:1. <math>|H|=[E:E^H]</math> | :1. <math>|H|=[E:E^H]</math> | ||
:2. <math>[E^H:F]=[G:H]</math> | :2. <math>[E^H:F]=[G:H]</math> | ||
| − | :3. <math>H_1\ | + | :3. <math>H_1\sube H_2</math> אם ורק אם <math>E^{H_1}\supe E^{H_2}</math> (אין טעות; כוון ההכלה מתהפך) |
| − | :4. <math>H</math> נורמלית ב-<math>G</math> אם ורק אם <math>E^H/F</math> נורמלית אם ורק אם <math>E^H/F</math> גלואה. במקרה זה | + | :4. <math>H</math> נורמלית ב-<math>G</math> אם ורק אם <math>E^H/F</math> נורמלית אם ורק אם <math>E^H/F</math> גלואה. במקרה זה <math>\text{Gal}(E^H/F)\cong G/H</math> . האיזומורפיזם נתון ע"י שליחת קוסט <math>\sigma H</math> אל <math>\sigma|_{E^H}</math> . |
'''הערה:''' קיים אנלוג של המשפט הנ"ל גם להרחבות גלואה אינסופיות. | '''הערה:''' קיים אנלוג של המשפט הנ"ל גם להרחבות גלואה אינסופיות. | ||
| + | ==חישוב בידיים של ההתאמה== | ||
| + | נניח כי <math>E/F</math> הרחבת גלואה מממד סופי ומצאנו את חבורת גלואה <math>G=\text{Gal}(E/F)</math> . | ||
| − | == | + | בהינתן שדה <math>F\sube K\sube E</math> קל למצוא את תת החבורה המתאימה לו <math>H=\text{Gal}(E/K)</math> ע"י בדיקה אילו מאברי <math>G</math> מייצבים את <math>K</math> . בפרט, אם <math>K=F[a_1,\ldots,a_n]</math> מספיק לבדוק אילו מאברי <math>G</math> מייצבים את <math>a_1,\ldots,a_n</math> . |
| − | + | לעומת זאת, בהינתן תת־חבורה <math>H\le G</math> לא תמיד ברור מהו תת־השדה המתאים לה <math>K=E^H</math> . | |
| − | + | ראשית, נשים לב שהתנאי <math>a\in E^H</math> אומר <math>\sigma a=a</math> לכל <math>\sigma\in H</math> . היות וכל <math>\sigma\in H</math> היא העתקה לינארית מעל <math>F</math> , התנאים <math>\{\sigma a=a\}_{\sigma\in H}</math> שקולים למשוואות לינאריות מעל <math>F</math> . בסיס למרחב הפתרונות יהיה בסיס ל־<math>E^H</math> מעל <math>F</math> . | |
| − | + | שימו לב שכדי לתרגם משוואה מהצורה <math>\sigma a=a</math> למשוואה לינארית מעל <math>F</math> יש לבחור בסיס ל־<math>E</math> כמרחב וקטורי מעל <math>F</math> . (הנעלמים יהיו הסקלרים אותם נכפיל באברי הבסיס.) | |
| − | + | השיטה הנ"ל אמנם תמיד עובדת, אך בדרך כלל אורכת זמן לביצוע. לכן, אם אפשר עדיף לנסות למצוא אברים <math>a_1,\ldots,a_n\in E^H</math> ולקוות שהם יוצרים את <math>E^H</math> מעל <math>F</math> . כעת יש שתי שאלות: איך נמצא את האברים ואיך נדע שהם יוצרים את <math>E^H</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | השיטה הנ"ל אמנם תמיד | + | |
תשובה לשאלה השנייה נובעת מהטענה הבאה: | תשובה לשאלה השנייה נובעת מהטענה הבאה: | ||
| − | '''טענה:''' <math>E^H=F[a_1,\ | + | '''טענה:''' <math>E^H=F[a_1,\ldots,a_n]</math> אם ורק אם <math>H</math> מייצבת את <math>a_1,\ldots,a_n</math> וגם <math>[F[a_1,\ldots,a_n]:F]\ge[G:H]</math> . |
'''הוכחה:''' תרגיל בעזרת המשפט היסודי של תורת גלואה. | '''הוכחה:''' תרגיל בעזרת המשפט היסודי של תורת גלואה. | ||
| − | לשאלה הראשונה אין תשובה פורמלית (חוץ מלפתור משוואות). לפעמים ברור | + | לשאלה הראשונה אין תשובה פורמלית (חוץ מלפתור משוואות). לפעמים ברור שאברים הם ב־<math>E^H</math> והם גם מספיקים כדי ליצור את כולו. להלן שתי דוגמאות: |
| − | :1. אם <math>\sigma</math> הוא צמצום של הצמוד המרוכב, אז כל מספר ממשי | + | :1. אם <math>\sigma</math> הוא צמצום של הצמוד המרוכב, אז כל מספר ממשי ב־<math>E</math> נמצא ב־<math>E^\sigma</math> . |
| − | :2. נניח | + | :2. נניח כי <math>E</math> שדה פיצול של <math>f</math> מעל <math>F</math> ויהיו <math>a_1,\ldots,a_k\in E</math> השורשים של <math>f</math> . אזי ניתן לחשוב על אברי <math>G</math> כתמורות ב־<math>S_k</math> (המתאימות לתמורות על השורשים <math>a_1,\ldots,a_k</math>). נשים לב שאם <math>\sigma\in H</math> היא מכפלה של מחזורים זרים שאחד מהם הוא <math>(n_1,\ldots,n_r)</math> אז <math>\sum\limits_{i=1}^ra_{n_i},~\prod\limits_{i=1}^ra_{n_i}\in E^{<\sigma>}</math> . |
| − | :3. באותן הנחות כמו | + | :3. באותן הנחות כמו ב־2, אם האינדקס <math>n</math> לא מופיע בייצוג של <math>\sigma\in H</math> כמכפלת מחזורים זרים, אז <math>\sigma a_n=a_n</math> . |
| − | '''דוגמא:''' נניח | + | '''דוגמא:''' נניח כי <math>E=\Q[\sqrt[4]{2},i],~F=\Q</math> . ההרחבה <math>E/F</math> חבורת גלואה ונוצרת ע"י שתי העתקות <math>\sigma,\alpha</math> הנתונות ע"י: |
| − | : <math>\sigma(i)=-i,~\sigma(\sqrt[4]{2})=\sqrt[4]{2} | + | :<math>\begin{align}\sigma(i)&=-i,~\sigma(\sqrt[4]{2})=\sqrt[4]{2}\\\alpha(i)&=i,~\alpha(\sqrt[4]{2})=i\sqrt[4]{2}\end{align}</math> |
| − | + | האברים <math>\sigma,\alpha</math> מקיימים את היחסים <math>\alpha^4=\sigma^2=id,\alpha\sigma=\alpha^-1\sigma</math> (עם עוד קצת נימוקים זה מספיק כדי להראות כי <math>\text{Gal}(E/F)\cong D_4</math>). בדקו שהחבורה <math><\sigma\alpha></math> מכילה שני אברים. | |
| − | + | ||
| − | כדי למצוא את <math>E^{<\sigma\alpha>}</math> נזכר | + | כדי למצוא את <math>E^{<\sigma\alpha>}</math> נזכר כי <math>E</math> שדה פיצול של <math>x^4-2</math> ושורשי הפולינום הם <math>\sqrt[4]{2},i\sqrt[4]{2},-\sqrt[4]{2},-i\sqrt[4]{2}</math> נסמן אותם ב־<math>a_1,a_2,a_3,a_4</math> בהתאמה. כעת, התמורה המתאימה ל־<math>\sigma\alpha</math> היא <math>(1,4)(2,3)</math> . לכן <math>b=a_1+a_4\in E^H</math> . |
| − | נבדוק האם <math>\ | + | נבדוק האם <math>\Q[b]=E^H</math> . מתקיים <math>b=\sqrt[4]{2}-i\sqrt[4]{2}=(1-i)\sqrt[4]{2}=\rho_8^3\sqrt[4]{8}</math> באשר |
| + | <math>\rho_8=e^{\frac{2\pi}{8}i}</math> . לכן <math>b</math> שורש של <math>x^4+8</math> (במובן מסוים <math>b=\sqrt[4]{-8}</math> אם כי הניסוח הזה לא אומר באיזה שורש מדובר). נשאיר את זה כתרגיל לבדוק שמדובר בפולינום אי פריק (רמז: הציבו <math>x=2y^{-1}</math>). לכן ההרחבה <math>\Q[b]/\Q</math> היא ממעלה 4. אבל <math>[E^{<\sigma\alpha>}:\Q]=[G:<\sigma\alpha>]=4</math> ולכן <math>E^{<\sigma\alpha>}=\Q[\rho_8^3\sqrt[4]{8}]</math> . | ||
'''דוגמא:''' בסימונים של הדוגמא הקודמת, מהו <math>E^{<\sigma\alpha^2>}</math>? | '''דוגמא:''' בסימונים של הדוגמא הקודמת, מהו <math>E^{<\sigma\alpha^2>}</math>? | ||
| − | תשובה: התמורה המתאימה | + | תשובה: התמורה המתאימה ל־<math>\sigma^2\alpha</math> היא <math>(1,3)</math> . לכן <math>i\sqrt[4]{2}=a_2\in E^{<\sigma\alpha^2>}</math> . אותם שיקולי ממד מהדוגמא הקודמת יראו כי <math>E^{<\sigma\alpha^2>}=\Q[i\sqrt[4]{2}]</math> . |
| − | + | ||
| − | + | ||
| + | ==בסיסים נורמליים ואיך להשתמש בהם== | ||
בקרוב... אלא אם אחד הסטודנטים מתנדב לכתוב בעצמו את הערך הזה. | בקרוב... אלא אם אחד הסטודנטים מתנדב לכתוב בעצמו את הערך הזה. | ||
[[קטגוריה:תורת גלואה]] | [[קטגוריה:תורת גלואה]] | ||
גרסה אחרונה מ־13:56, 2 בספטמבר 2018
התאמת גלואה היא הלב של תורת גלואה ועליה מושתתות הרבה תוצאות חשובות. ההתאמה מתבטאת במשפט היסודי של תורת גלואה הקובע כי יש התאמה בין שדות ביניים של הרחבת גלואה ובין תתי החבורות של חבורת גלואה שלה.
המשפט היסודי של תורת גלואה
משפט: תהי 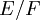 הרחבת גלואה מממד סופי ותהי
הרחבת גלואה מממד סופי ותהי 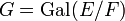 אזי קיימת התאמה חח"ע ועל בין:
אזי קיימת התאמה חח"ע ועל בין:
- א. תת־שדות
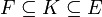
- ב. תת־חבורות
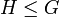
ההתאמה שולחת חבורה 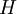 אל השדה
אל השדה 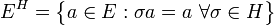 ותת־שדה
ותת־שדה 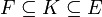 אל החבורה
אל החבורה 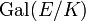 (פונקציות אלו הפוכות זו לזו). בנוסף, ההתאמה מקיימת:
(פונקציות אלו הפוכות זו לזו). בנוסף, ההתאמה מקיימת:
- 1.
![|H|=[E:E^H]](/images/math/8/0/7/807195dea432887ac2a3e332cb4eb6ac.png)
- 2.
![[E^H:F]=[G:H]](/images/math/4/6/3/46382ee09231f9b65c66cd5ee60ec40d.png)
- 3.
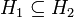 אם ורק אם
אם ורק אם 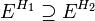 (אין טעות; כוון ההכלה מתהפך)
(אין טעות; כוון ההכלה מתהפך) - 4.
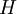 נורמלית ב-
נורמלית ב- אם ורק אם
אם ורק אם 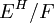 נורמלית אם ורק אם
נורמלית אם ורק אם 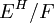 גלואה. במקרה זה
גלואה. במקרה זה 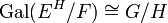 . האיזומורפיזם נתון ע"י שליחת קוסט
. האיזומורפיזם נתון ע"י שליחת קוסט 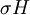 אל
אל 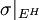 .
.
הערה: קיים אנלוג של המשפט הנ"ל גם להרחבות גלואה אינסופיות.
חישוב בידיים של ההתאמה
נניח כי 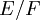 הרחבת גלואה מממד סופי ומצאנו את חבורת גלואה
הרחבת גלואה מממד סופי ומצאנו את חבורת גלואה 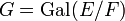 .
.
בהינתן שדה 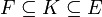 קל למצוא את תת החבורה המתאימה לו
קל למצוא את תת החבורה המתאימה לו 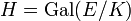 ע"י בדיקה אילו מאברי
ע"י בדיקה אילו מאברי  מייצבים את
מייצבים את  . בפרט, אם
. בפרט, אם ![K=F[a_1,\ldots,a_n]](/images/math/5/9/e/59ef976d320eb1f4f6aa8732cb781dac.png) מספיק לבדוק אילו מאברי
מספיק לבדוק אילו מאברי  מייצבים את
מייצבים את 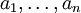 .
.
לעומת זאת, בהינתן תת־חבורה 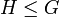 לא תמיד ברור מהו תת־השדה המתאים לה
לא תמיד ברור מהו תת־השדה המתאים לה 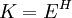 .
.
ראשית, נשים לב שהתנאי 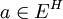 אומר
אומר 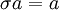 לכל
לכל 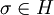 . היות וכל
. היות וכל 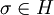 היא העתקה לינארית מעל
היא העתקה לינארית מעל  , התנאים
, התנאים 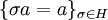 שקולים למשוואות לינאריות מעל
שקולים למשוואות לינאריות מעל  . בסיס למרחב הפתרונות יהיה בסיס ל־
. בסיס למרחב הפתרונות יהיה בסיס ל־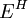 מעל
מעל  .
.
שימו לב שכדי לתרגם משוואה מהצורה 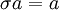 למשוואה לינארית מעל
למשוואה לינארית מעל  יש לבחור בסיס ל־
יש לבחור בסיס ל־ כמרחב וקטורי מעל
כמרחב וקטורי מעל  . (הנעלמים יהיו הסקלרים אותם נכפיל באברי הבסיס.)
. (הנעלמים יהיו הסקלרים אותם נכפיל באברי הבסיס.)
השיטה הנ"ל אמנם תמיד עובדת, אך בדרך כלל אורכת זמן לביצוע. לכן, אם אפשר עדיף לנסות למצוא אברים 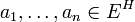 ולקוות שהם יוצרים את
ולקוות שהם יוצרים את 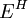 מעל
מעל  . כעת יש שתי שאלות: איך נמצא את האברים ואיך נדע שהם יוצרים את
. כעת יש שתי שאלות: איך נמצא את האברים ואיך נדע שהם יוצרים את 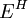 .
.
תשובה לשאלה השנייה נובעת מהטענה הבאה:
טענה: ![E^H=F[a_1,\ldots,a_n]](/images/math/b/6/f/b6fe5b703662f43007c25db89036a394.png) אם ורק אם
אם ורק אם 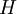 מייצבת את
מייצבת את 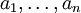 וגם
וגם ![[F[a_1,\ldots,a_n]:F]\ge[G:H]](/images/math/0/9/5/09598ff6fea5d6ceffb3815ebf89bed8.png) .
.
הוכחה: תרגיל בעזרת המשפט היסודי של תורת גלואה.
לשאלה הראשונה אין תשובה פורמלית (חוץ מלפתור משוואות). לפעמים ברור שאברים הם ב־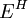 והם גם מספיקים כדי ליצור את כולו. להלן שתי דוגמאות:
והם גם מספיקים כדי ליצור את כולו. להלן שתי דוגמאות:
- 1. אם
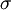 הוא צמצום של הצמוד המרוכב, אז כל מספר ממשי ב־
הוא צמצום של הצמוד המרוכב, אז כל מספר ממשי ב־ נמצא ב־
נמצא ב־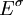 .
. - 2. נניח כי
 שדה פיצול של
שדה פיצול של  מעל
מעל  ויהיו
ויהיו 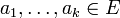 השורשים של
השורשים של  . אזי ניתן לחשוב על אברי
. אזי ניתן לחשוב על אברי  כתמורות ב־
כתמורות ב־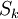 (המתאימות לתמורות על השורשים
(המתאימות לתמורות על השורשים 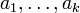 ). נשים לב שאם
). נשים לב שאם 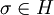 היא מכפלה של מחזורים זרים שאחד מהם הוא
היא מכפלה של מחזורים זרים שאחד מהם הוא 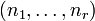 אז
אז 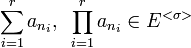 .
. - 3. באותן הנחות כמו ב־2, אם האינדקס
 לא מופיע בייצוג של
לא מופיע בייצוג של 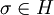 כמכפלת מחזורים זרים, אז
כמכפלת מחזורים זרים, אז 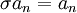 .
.
דוגמא: נניח כי ![E=\Q[\sqrt[4]{2},i],~F=\Q](/images/math/b/2/9/b29cebf8dafead4e4a16f2f86aaa6e5f.png) . ההרחבה
. ההרחבה 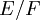 חבורת גלואה ונוצרת ע"י שתי העתקות
חבורת גלואה ונוצרת ע"י שתי העתקות 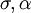 הנתונות ע"י:
הנתונות ע"י:
האברים 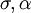 מקיימים את היחסים
מקיימים את היחסים 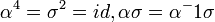 (עם עוד קצת נימוקים זה מספיק כדי להראות כי
(עם עוד קצת נימוקים זה מספיק כדי להראות כי 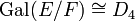 ). בדקו שהחבורה
). בדקו שהחבורה 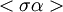 מכילה שני אברים.
מכילה שני אברים.
כדי למצוא את 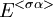 נזכר כי
נזכר כי  שדה פיצול של
שדה פיצול של 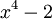 ושורשי הפולינום הם
ושורשי הפולינום הם ![\sqrt[4]{2},i\sqrt[4]{2},-\sqrt[4]{2},-i\sqrt[4]{2}](/images/math/6/f/b/6fbc1558a0731c6c6b2d8d952fc25d7a.png) נסמן אותם ב־
נסמן אותם ב־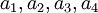 בהתאמה. כעת, התמורה המתאימה ל־
בהתאמה. כעת, התמורה המתאימה ל־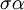 היא
היא 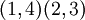 . לכן
. לכן 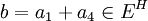 .
.
נבדוק האם ![\Q[b]=E^H](/images/math/1/2/d/12deda7d9291502b694baa27750acc8c.png) . מתקיים
. מתקיים ![b=\sqrt[4]{2}-i\sqrt[4]{2}=(1-i)\sqrt[4]{2}=\rho_8^3\sqrt[4]{8}](/images/math/1/e/6/1e62c0edc462534453c22384b81f7570.png) באשר
באשר
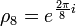 . לכן
. לכן 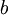 שורש של
שורש של 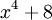 (במובן מסוים
(במובן מסוים ![b=\sqrt[4]{-8}](/images/math/e/8/8/e88c95e00ef271f1422afda62d662db5.png) אם כי הניסוח הזה לא אומר באיזה שורש מדובר). נשאיר את זה כתרגיל לבדוק שמדובר בפולינום אי פריק (רמז: הציבו
אם כי הניסוח הזה לא אומר באיזה שורש מדובר). נשאיר את זה כתרגיל לבדוק שמדובר בפולינום אי פריק (רמז: הציבו 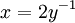 ). לכן ההרחבה
). לכן ההרחבה ![\Q[b]/\Q](/images/math/8/1/c/81c1f0a0dd97f024b0cf792ba7aa893c.png) היא ממעלה 4. אבל
היא ממעלה 4. אבל ![[E^{<\sigma\alpha>}:\Q]=[G:<\sigma\alpha>]=4](/images/math/f/f/a/ffaa1d57791759d15f921b360e91c726.png) ולכן
ולכן ![E^{<\sigma\alpha>}=\Q[\rho_8^3\sqrt[4]{8}]](/images/math/e/e/5/ee5d459449efb0d01eb5563e0199bbde.png) .
.
דוגמא: בסימונים של הדוגמא הקודמת, מהו 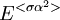 ?
?
תשובה: התמורה המתאימה ל־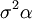 היא
היא 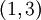 . לכן
. לכן ![i\sqrt[4]{2}=a_2\in E^{<\sigma\alpha^2>}](/images/math/a/d/2/ad2a70df616aad2001bfcfdd3b9c9009.png) . אותם שיקולי ממד מהדוגמא הקודמת יראו כי
. אותם שיקולי ממד מהדוגמא הקודמת יראו כי ![E^{<\sigma\alpha^2>}=\Q[i\sqrt[4]{2}]](/images/math/f/6/7/f67d2708b99b843f2f4e89e6b9d62156.png) .
.
בסיסים נורמליים ואיך להשתמש בהם
בקרוב... אלא אם אחד הסטודנטים מתנדב לכתוב בעצמו את הערך הזה.
![\begin{align}\sigma(i)&=-i,~\sigma(\sqrt[4]{2})=\sqrt[4]{2}\\\alpha(i)&=i,~\alpha(\sqrt[4]{2})=i\sqrt[4]{2}\end{align}](/images/math/6/c/3/6c3e9c443280f6011f9ff144aaaf3ed3.png)