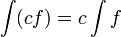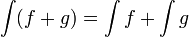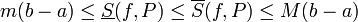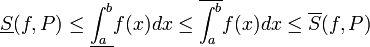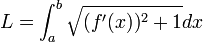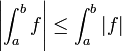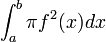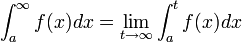הבדלים בין גרסאות בדף "חדוא 2 - ארז שיינר"
מתוך Math-Wiki
(←מבחני השוואה לאינטגרלים חיוביים) |
(←מבחן דיריכלה) |
||
| שורה 152: | שורה 152: | ||
===מבחן דיריכלה=== | ===מבחן דיריכלה=== | ||
| + | *תהי פונקציה <math>f</math> אשר מקיימת 3 תנאים בקטע <math>[a,\infty)</math> | ||
| + | **<math>f</math> מונוטונית יורדת | ||
| + | **<math>\lim_{x\to\infty}f(x)=0</math> | ||
| + | **הנגזרת <math>f'</math> רציפה. | ||
| + | *תהי בנוסף פונקציה <math>g</math> אשר מקיימת 2 תנאים באותו הקטע: | ||
| + | **<math>g</math> רציפה. | ||
| + | **ל<math>g</math> יש קדומה <math>G</math> חסומה. | ||
| + | *אזי האינטגרל <math>\int_a^\infty f(x)dx</math> מתכנס. | ||
<videoflash>wU73--emtSg</videoflash> | <videoflash>wU73--emtSg</videoflash> | ||
גרסה מ־11:07, 6 באפריל 2020
תוכן עניינים
תקציר ההרצאות
פרק 1 - האינטגרל הלא מסויים
- הגדרה: F נקראת פונקציה קדומה של f בקטע A אם לכל נקודה בקטע מתקיים כי
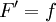
- האינטגרל הלא מסויים
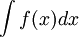 מסמן פונקציה קדומה של f.
מסמן פונקציה קדומה של f.
- תהי F קדומה של f, אזי קבוצת כל הקדומות של f שווה ל
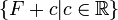
- אינטגרלים מיידיים ידועים לנו מנוסחאות הגזירה.
שיטות למציאת קדומה
- תהיינה f,g פונקציות בעלות קדומות, אזי:
אינטגרציה בחלקים
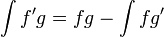
שיטת הההצבה
פונקציה רציונאלית
- הורדת דרגת המונה ע"י חילוק פולינומים
- פירוק לשברים חלקיים
- חישוב אינטגרל של כל שבר חלקי
- נסמן
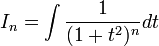
- אזי
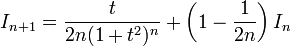
- נסמן
כאשר תנאי ההתחלה הוא 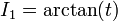
הצבות אוניברסאליות
הצבות אוניברסאליות הוא כינוי כללי להצבות המעבירות פונקציות ממשפחה מסוימת לצורה של פונקציה רציונאלית אותה אנחנו יודעים לפתור. שימו לב שכיון ופתרון פונקציה רציונאלית דורש פירוק פולינומים, לעתים המעבר לפונקציה רציונאלית לא יקדם אותנו לקראת פתרון הבעיה.
פרק 2 - האינטגרל המסויים
סכומי דרבו ואינטגרל עליון ותחתון
הגדרת סכומי דרבו, אינטגרביליות והאינטגרל המסוים
תכונות של סכומי דרבו והאינטגרל המסוים
- תהי חלוקה
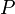 ותהי העדנה שלה
ותהי העדנה שלה 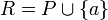
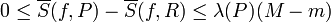
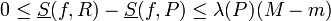
התכנסות סכומי דרבו
- התכנסות סכומי הדרבו העליונים לאינטגרל העליון
פונקציות אינטגרביליות
- פונקציה רציפה בקטע סגור אינטגרבילית בו
- פונקציה חסומה בקטע סופי, ורציפה פרט למספר סופי של נקודות, אינטגרבילית בו
סכומי רימן
- אינטגרביליות לפי רימן שקולה לאינטגרביליות לפי דרבו
אורך עקומה
אי שיוויון המשולש לאינטגרלים
פרק 3 - הקשר בין האינטגרל המסויים ללא מסויים
המשפט היסודי של החדו"א
- עבור פונקציה אינטגרבילית, בנקודות בהן היא רציפה מתקיים כי
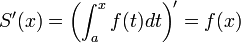
נוסחאת ניוטון לייבניץ
- תהי f אינטגרבילים וF קדומה אזי
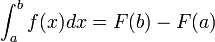
הגדרת המספר 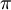 , וחישוב היקף ושטח מעגל
, וחישוב היקף ושטח מעגל
נפח גוף סיבוב
פרק 4 - אינטגרלים לא אמיתיים (מוכללים)
השופר של גבריאל
הגדרת אינטגרלים לא אמיתיים
- תהי f אינטגרבילית בקטע
![[a,t]](/images/math/4/1/d/41db424f5c02cc7c51f1f480735df0e4.png) לכל
לכל 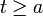 אזי:
אזי:
- תהי f שאינה חסומה בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ואינטגרבילית בקטע
ואינטגרבילית בקטע ![[t,b]](/images/math/6/6/c/66ce2d41698b246a23f9e4be3153c8cf.png) לכל
לכל 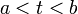 אזי:
אזי:
מבחני השוואה לאינטגרלים חיוביים
- מבחן ההשוואה הראשון:
- תהיינה
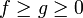 עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית אזי-
עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית אזי- - אם
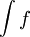 מתכנס בקטע, גם
מתכנס בקטע, גם 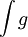 מתכנס בקטע
מתכנס בקטע
- תהיינה
- מבחן ההשוואה הגבולי:
- תהיינה
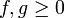 עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית.
עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית. - נחשב בנוסף את הגבול בנקודה הבעייתית
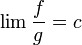 .
. - אזי:
- אם
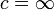 , אזי אם
, אזי אם 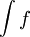 מתכנס גם
מתכנס גם 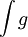 מתכנס.
מתכנס. - אם
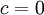 אזי אם
אזי אם 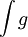 מתכנס גם
מתכנס גם 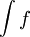 מתכנס.
מתכנס. - אם
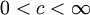 אזי האינטגרלים חברים
אזי האינטגרלים חברים 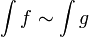 כלומר שניהם מתכנסים או שניהם מתבדרים.
כלומר שניהם מתכנסים או שניהם מתבדרים.
- אם
- תהיינה
התכנסות בהחלט וקריטריון היינה
מבחן דיריכלה
- תהי פונקציה
 אשר מקיימת 3 תנאים בקטע
אשר מקיימת 3 תנאים בקטע 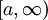
 מונוטונית יורדת
מונוטונית יורדת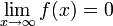
- הנגזרת
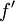 רציפה.
רציפה.
- תהי בנוסף פונקציה
 אשר מקיימת 2 תנאים באותו הקטע:
אשר מקיימת 2 תנאים באותו הקטע:
 רציפה.
רציפה.- ל
 יש קדומה
יש קדומה  חסומה.
חסומה.
- אזי האינטגרל
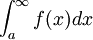 מתכנס.
מתכנס.