הבדלים בין גרסאות בדף "חוג הפולינומים מעל שדה"
Tomer Yogev (שיחה | תרומות) (←תכונות) |
מ (←הגדרה) |
||
| שורה 3: | שורה 3: | ||
יהי <math>F</math> שדה. ביטוי פורמלי מהצורה <math>\sum_{i=0}^na_ix^i=a_0+a_1x+\ldots+a_nx^n</math> כאשר <math>n\geq0</math> ו-<math>a_1,\ldots,a_n\in F</math> נקרא '''פולינום במשתנה <math>x</math> מעל <math>F</math>'''. האיברים <math>a_0,\ldots,a_n</math> נקראים '''מקדמי הפולינום'''. | יהי <math>F</math> שדה. ביטוי פורמלי מהצורה <math>\sum_{i=0}^na_ix^i=a_0+a_1x+\ldots+a_nx^n</math> כאשר <math>n\geq0</math> ו-<math>a_1,\ldots,a_n\in F</math> נקרא '''פולינום במשתנה <math>x</math> מעל <math>F</math>'''. האיברים <math>a_0,\ldots,a_n</math> נקראים '''מקדמי הפולינום'''. | ||
| − | נניח כי <math>m\leq n</math> אנו נאמר כי שני פולינומים <math>\sum_{i=0}^na_ix^i,\,\sum_{j=1}^mb_jx^j</math> הם שקולים אם <math>a_i=b_i</math> עבור <math>0\leq i\leq m</math> ו-<math>a_i=0</math> עבור <math>m<i\leq n</math>. מעכשיו, כאשר נדבר על פולינום נתכוון | + | נניח כי <math>m\leq n</math> אנו נאמר כי שני פולינומים <math>\sum_{i=0}^na_ix^i,\,\sum_{j=1}^mb_jx^j</math> הם שקולים אם <math>a_i=b_i</math> עבור <math>0\leq i\leq m</math> ו-<math>a_i=0</math> עבור <math>m<i\leq n</math>. מעכשיו, כאשר נדבר על פולינום נתכוון בעצם למחלקת השקילות של כל הפולינומים השקולים לו. עדיף לא לחשוב על זה. |
כל פולינום <math>f(x)</math> שאינו פולינום ה-0 (פולינום שכל מקדמיו הם 0) שקול לפולינום יחיד <math>a_0+a_1x+\ldots+a_nx^n</math> עם <math>a_n\neq 0</math>. המספר <math>n</math> נקרא '''דרגת הפולינום''' ומסומן ב-<math>\deg f</math>. מעלת פולינום ה-0 מוגדרת לעיתים להיות <math>-\infty</math>. | כל פולינום <math>f(x)</math> שאינו פולינום ה-0 (פולינום שכל מקדמיו הם 0) שקול לפולינום יחיד <math>a_0+a_1x+\ldots+a_nx^n</math> עם <math>a_n\neq 0</math>. המספר <math>n</math> נקרא '''דרגת הפולינום''' ומסומן ב-<math>\deg f</math>. מעלת פולינום ה-0 מוגדרת לעיתים להיות <math>-\infty</math>. | ||
| שורה 12: | שורה 12: | ||
'''אוסף הפולינומים מעל <math>F</math> במשתנה <math>x</math>''' יסומן ב-<math>F[x]</math>. | '''אוסף הפולינומים מעל <math>F</math> במשתנה <math>x</math>''' יסומן ב-<math>F[x]</math>. | ||
מגידירים על <math>F[x]</math> חיבור וכפל על ידי הנוסחאות: | מגידירים על <math>F[x]</math> חיבור וכפל על ידי הנוסחאות: | ||
| − | * <math>\sum_{i=0}^na_ix^i+\sum_{i= | + | * <math>\sum_{i=0}^na_ix^i+\sum_{i=0}^nb_ix^n=\sum_{i=0}^n(a_i+b_i)x^n</math> (אם דרגת הפולינומים שמחברים לא שווה החליפו אותם בפולינומים שקולים עם אותה דרגה.) |
* <math>\sum_{i=0}^na_ix^i\cdot\sum_{j=0}^mb_jx^j=\sum_{k=0}^{m+n}\left(\sum_{0\leq i\leq n,0\leq j\leq m,m+n=k}a_ib_j\right)x^k</math> | * <math>\sum_{i=0}^na_ix^i\cdot\sum_{j=0}^mb_jx^j=\sum_{k=0}^{m+n}\left(\sum_{0\leq i\leq n,0\leq j\leq m,m+n=k}a_ib_j\right)x^k</math> | ||
הפעולות האלה הופכות את <math>F[x]</math> לחוג. | הפעולות האלה הופכות את <math>F[x]</math> לחוג. | ||
'''הערה:''' כל ההגדרות לעיל עובדות לכל חוג ולא רק לשדות. | '''הערה:''' כל ההגדרות לעיל עובדות לכל חוג ולא רק לשדות. | ||
| − | |||
== תכונות == | == תכונות == | ||
גרסה אחרונה מ־12:53, 20 ביולי 2013
הגדרה
יהי  שדה. ביטוי פורמלי מהצורה
שדה. ביטוי פורמלי מהצורה 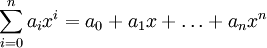 כאשר
כאשר 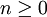 ו-
ו-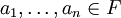 נקרא פולינום במשתנה
נקרא פולינום במשתנה  מעל
מעל  . האיברים
. האיברים 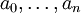 נקראים מקדמי הפולינום.
נקראים מקדמי הפולינום.
נניח כי 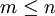 אנו נאמר כי שני פולינומים
אנו נאמר כי שני פולינומים 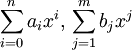 הם שקולים אם
הם שקולים אם 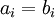 עבור
עבור 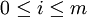 ו-
ו-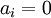 עבור
עבור 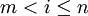 . מעכשיו, כאשר נדבר על פולינום נתכוון בעצם למחלקת השקילות של כל הפולינומים השקולים לו. עדיף לא לחשוב על זה.
. מעכשיו, כאשר נדבר על פולינום נתכוון בעצם למחלקת השקילות של כל הפולינומים השקולים לו. עדיף לא לחשוב על זה.
כל פולינום  שאינו פולינום ה-0 (פולינום שכל מקדמיו הם 0) שקול לפולינום יחיד
שאינו פולינום ה-0 (פולינום שכל מקדמיו הם 0) שקול לפולינום יחיד 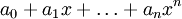 עם
עם 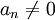 . המספר
. המספר  נקרא דרגת הפולינום ומסומן ב-
נקרא דרגת הפולינום ומסומן ב-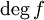 . מעלת פולינום ה-0 מוגדרת לעיתים להיות
. מעלת פולינום ה-0 מוגדרת לעיתים להיות 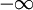 .
.
הערה: כל פולינום 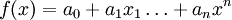 משרה פונקציה מ-
משרה פונקציה מ- לעצמו ששולחת את
לעצמו ששולחת את 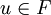 ל-
ל-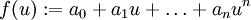 . אם השדה
. אם השדה  סופי, ייתכן כי שני פולינומים שונים ישרו אותה פונקציה.
סופי, ייתכן כי שני פולינומים שונים ישרו אותה פונקציה.
אוסף הפולינומים מעל  במשתנה
במשתנה  יסומן ב-
יסומן ב-![F[x]](/images/math/6/f/a/6fa9279fd5ecaf11f6c30b8b18f593bf.png) .
מגידירים על
.
מגידירים על ![F[x]](/images/math/6/f/a/6fa9279fd5ecaf11f6c30b8b18f593bf.png) חיבור וכפל על ידי הנוסחאות:
חיבור וכפל על ידי הנוסחאות:
-
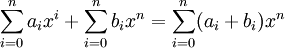 (אם דרגת הפולינומים שמחברים לא שווה החליפו אותם בפולינומים שקולים עם אותה דרגה.)
(אם דרגת הפולינומים שמחברים לא שווה החליפו אותם בפולינומים שקולים עם אותה דרגה.) -
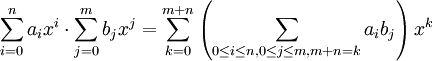
הפעולות האלה הופכות את ![F[x]](/images/math/6/f/a/6fa9279fd5ecaf11f6c30b8b18f593bf.png) לחוג.
לחוג.
הערה: כל ההגדרות לעיל עובדות לכל חוג ולא רק לשדות.
תכונות
אם  שדה, החוג
שדה, החוג ![F[x]](/images/math/6/f/a/6fa9279fd5ecaf11f6c30b8b18f593bf.png) הוא תחום אוקלידי. פונקציית הדרגה תהייה דרגת הפולינום. כתוצאה מכך:
הוא תחום אוקלידי. פונקציית הדרגה תהייה דרגת הפולינום. כתוצאה מכך:
- לכל שני פולינומים קיים מחלק משותף מקסימלי וניתן למצוא אותן ע"י האלגוריתם של אוקלידס.
-
![F[x]](/images/math/6/f/a/6fa9279fd5ecaf11f6c30b8b18f593bf.png) תחום ראשי, כלומר כל אידיאל נוצר ע"י איבר אחד. אם האידיאל אינו 0, האיבר הזה הוא בעל דרגה מינימלית באידיאל (אם מתעלמים מפולינום ה-0).
תחום ראשי, כלומר כל אידיאל נוצר ע"י איבר אחד. אם האידיאל אינו 0, האיבר הזה הוא בעל דרגה מינימלית באידיאל (אם מתעלמים מפולינום ה-0). -
![F[x]](/images/math/6/f/a/6fa9279fd5ecaf11f6c30b8b18f593bf.png) הוא תחום פריקות יחידה (לכל פולינום יש פירוק יחיד לגורמים)
הוא תחום פריקות יחידה (לכל פולינום יש פירוק יחיד לגורמים) - פולינום שונה מ-0 הוא אי-פריק אם ורק אם הוא ראשוני.
- כל אידיאל ראשוני שונה מ-0 של
![F[x]](/images/math/6/f/a/6fa9279fd5ecaf11f6c30b8b18f593bf.png) הוא מקסימלי. בפרט, אם
הוא מקסימלי. בפרט, אם 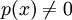 הוא ראשוני (או אי פריק) אז
הוא ראשוני (או אי פריק) אז ![F[x]/p(x)F[x]](/images/math/4/3/4/434edc1e17ca646bfa0d95adfa6ed402.png) הוא שדה.
הוא שדה.