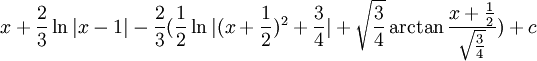הבדלים בין גרסאות בדף "חשבון אינפיניטיסימלי 2 - פתרון מועד א תשע"ג"
מתוך Math-Wiki
איתמר שטיין (שיחה | תרומות) (←סעיף ב) |
איתמר שטיין (שיחה | תרומות) (←סעיף ב) |
||
| שורה 54: | שורה 54: | ||
<math>=\frac{1}{2}\int\frac{2t}{t^2+\frac{3}{4}}\mathrm{d}t+\int\frac{\frac{3}{4}}{t^2+\frac{3}{4}}\mathrm{d}t</math> | <math>=\frac{1}{2}\int\frac{2t}{t^2+\frac{3}{4}}\mathrm{d}t+\int\frac{\frac{3}{4}}{t^2+\frac{3}{4}}\mathrm{d}t</math> | ||
| − | <math>=\frac{1}{2}\ln | + | <math>=\frac{1}{2}\ln|t^2+\frac{3}{4}|+\frac{3}{4}\frac{1}{\sqrt{\frac{3}{4}}}\arctan\frac{t}{\sqrt{\frac{3}{4}}}+c</math> |
<math>=\frac{1}{2}\ln|(x+\frac{1}{2})^2+\frac{3}{4}|+\sqrt{\frac{3}{4}}\arctan\frac{x+\frac{1}{2}}{\sqrt{\frac{3}{4}}}+c</math> | <math>=\frac{1}{2}\ln|(x+\frac{1}{2})^2+\frac{3}{4}|+\sqrt{\frac{3}{4}}\arctan\frac{x+\frac{1}{2}}{\sqrt{\frac{3}{4}}}+c</math> | ||
גרסה מ־17:35, 8 ביולי 2013
שאלה 2
סעיף א
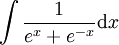
נציב 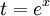 ואז
ואז 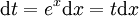
לאחר הצבה נקבל
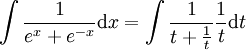
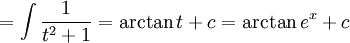
סעיף ב
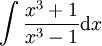
על ידי חילוק פולינומים קל לראות ש
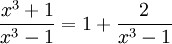
אז נתמקד בחישוב 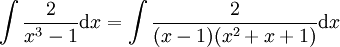
לפי האלגוריתם לחישוב אינטגרל של פונקציה רציונאלית נחפש
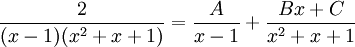
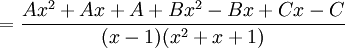
כלומר קיבלנו מערכת משוואות
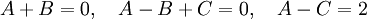
וקל לראות שהפתרון שלה הוא:
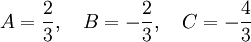
ברור ש
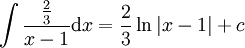
נותר לחשב את 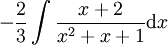
לפי השלמה לריבוע
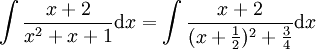
נבצע הצבה 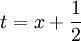 (רק בשביל נוחות) ואז נישאר עם
(רק בשביל נוחות) ואז נישאר עם
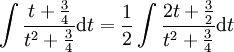
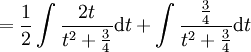
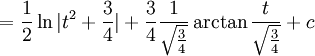
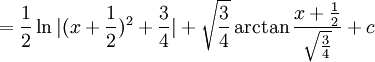
ולכן 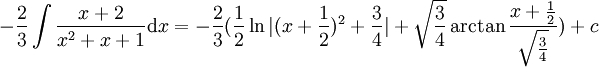
אם נסכום את כל מה שקיבלנו נקבל שהתוצאה היא