הבדלים בין גרסאות בדף "כלל לופיטל"
מתוך Math-Wiki
מ (משפטים/אינפי/כלל לופיטל הועבר לכלל לופיטל) |
|||
| שורה 1: | שורה 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
'''משפט:''' נניח כי <math>lim_{x\to a^+}f(x)=lim_{x\to a^+}g(x)=0</math> ונניח עוד כי <math>f,g</math> גזירות בסביבה ימנית של a ומתקיים <math>lim_{x\to a^+}=\frac{f'(x)}{g'(x)}=L</math> אז מתקיים <math>lim_{x\to a^+}=\frac{f(x)}{g(x)}=L</math> | '''משפט:''' נניח כי <math>lim_{x\to a^+}f(x)=lim_{x\to a^+}g(x)=0</math> ונניח עוד כי <math>f,g</math> גזירות בסביבה ימנית של a ומתקיים <math>lim_{x\to a^+}=\frac{f'(x)}{g'(x)}=L</math> אז מתקיים <math>lim_{x\to a^+}=\frac{f(x)}{g(x)}=L</math> | ||
| שורה 15: | שורה 11: | ||
ולכן נקבל <math>\lim_{x\to a^{+}}\frac{f(x)}{g(x)}=\lim_{x\to a^{+}}\frac{f'(c(x))}{g'(c(x))}=\lim_{c\to a^{+}}\frac{f'(c)}{g'(c)} </math> | ולכן נקבל <math>\lim_{x\to a^{+}}\frac{f(x)}{g(x)}=\lim_{x\to a^{+}}\frac{f'(c(x))}{g'(c(x))}=\lim_{c\to a^{+}}\frac{f'(c)}{g'(c)} </math> | ||
כרצוי השיוויון האחרון נובע מכך ש <math>a<c(x)<x</math> וממשפט הסנדויץ | כרצוי השיוויון האחרון נובע מכך ש <math>a<c(x)<x</math> וממשפט הסנדויץ | ||
| + | |||
| + | [[קטגוריה:אינפי]] | ||
גרסה מ־01:05, 15 בפברואר 2012
משפט: נניח כי 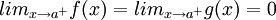 ונניח עוד כי
ונניח עוד כי 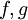 גזירות בסביבה ימנית של a ומתקיים
גזירות בסביבה ימנית של a ומתקיים 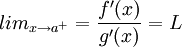 אז מתקיים
אז מתקיים 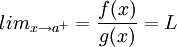
הוכחה: נוכל לבנות 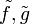 רציפות שמקיימות
רציפות שמקיימות 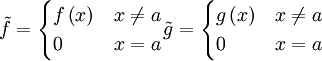 הגבול של מנתם בa יהיה זהה לגבול המקורי כי הוא נבדל ממנו רק בנקודה 1 לשם נוחות נמשיך לקרוא להם .f,g על פי משפט ערך הביניים של קושי עבור כל x בסביבה הימנית של a שבה f,g מוגדרות נוכל לבחור
הגבול של מנתם בa יהיה זהה לגבול המקורי כי הוא נבדל ממנו רק בנקודה 1 לשם נוחות נמשיך לקרוא להם .f,g על פי משפט ערך הביניים של קושי עבור כל x בסביבה הימנית של a שבה f,g מוגדרות נוכל לבחור 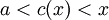 שמקיימת
שמקיימת 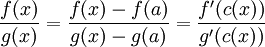 ולכן נקבל
ולכן נקבל 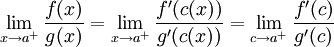 כרצוי השיוויון האחרון נובע מכך ש
כרצוי השיוויון האחרון נובע מכך ש 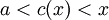 וממשפט הסנדויץ
וממשפט הסנדויץ