הבדלים בין גרסאות בדף "כלל לופיטל"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
שורה 1: שורה 1:
−
'''משפט:''' נניח כי <math>\lim_{x\to a^+}f(x)=\lim_{x\to a^+}g(x)=0</math> ונניח עוד כי <math>f,g</math> גזירות בסביבה ימנית של a ומתקיים <math>\lim_{x\to a^+}=\frac{f'(x)}{g'(x)}=L</math> אז מתקיים <math>\lim_{x\to a^+}=\frac{f(x)}{g(x)}=L</math>
+
=משפט לופיטל=
 +
נניח כי <math>\lim_{x\to a^+}f(x)=\lim_{x\to a^+}g(x)=0</math> ונניח עוד כי <math>f,g</math> גזירות בסביבה ימנית של a ומתקיים <math>\lim_{x\to a^+}=\frac{f'(x)}{g'(x)}=L</math> אז מתקיים <math>\lim_{x\to a^+}=\frac{f(x)}{g(x)}=L</math>
  
−
'''הוכחה:''' נוכל לבנות <math>\tilde{f},\tilde{g} </math> רציפות שמקיימות <math> \tilde{f}=\begin{cases}
+
==הוכחה==
 +
נוכל לבנות <math>\tilde{f},\tilde{g} </math> רציפות שמקיימות <math> \tilde{f}=\begin{cases}
 
f\left(x\right) & x\neq a\\
 
f\left(x\right) & x\neq a\\
 
0 & x=a
 
0 & x=a
שורה 11: שורה 13:
 
ולכן נקבל <math>\lim_{x\to a^{+}}\frac{f(x)}{g(x)}=\lim_{x\to a^{+}}\frac{f'(c(x))}{g'(c(x))}=\lim_{c\to a^{+}}\frac{f'(c)}{g'(c)} </math>
 
ולכן נקבל <math>\lim_{x\to a^{+}}\frac{f(x)}{g(x)}=\lim_{x\to a^{+}}\frac{f'(c(x))}{g'(c(x))}=\lim_{c\to a^{+}}\frac{f'(c)}{g'(c)} </math>
 
כרצוי השיוויון האחרון נובע מכך ש <math>a<c(x)<x</math> וממשפט הסנדויץ
 
כרצוי השיוויון האחרון נובע מכך ש <math>a<c(x)<x</math> וממשפט הסנדויץ
 +
 +
=שימוש בכלל לופיטל=
 +
 +
תהיינה שתי פונקציות f,g. ותהי נקודה <math>x_0\in\mathbb{R}</math> או <math>x_0=\pm\infty</math> כך ש
 +
:<math>\lim_{x\rightarrow x_0}f(x)=L</math>
 +
:<math>\lim_{x\rightarrow x_0}g(x)=M</math>
 +
 +
נראה כיצד ניתן להעזר בכלל לופיטל על מנת לחשב גבולות במקרים בהם משפטי האריתמטיקה הרגילים נכשלים.
 +
 +
== מקרה ראשון <math>\frac{0}{0}</math> או <math>\frac{\infty}{\infty}</math>==
 +
 +
  
 
[[קטגוריה:אינפי]]
 
[[קטגוריה:אינפי]]

גרסה מ־17:07, 22 בפברואר 2014

משפט לופיטל

נניח כי 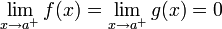\lim_{x\to a^+}f(x)=\lim_{x\to a^+}g(x)=0 ונניח עוד כי 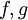f,g גזירות בסביבה ימנית של a ומתקיים 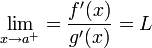\lim_{x\to a^+}=\frac{f'(x)}{g'(x)}=L אז מתקיים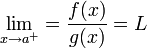 \lim_{x\to a^+}=\frac{f(x)}{g(x)}=L

הוכחה

נוכל לבנות 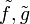\tilde{f},\tilde{g} רציפות שמקיימות 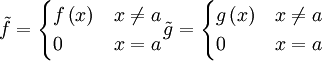\tilde{f}=\begin{cases} f\left(x\right) & x\neq a\\ 0 & x=a \end{cases} \tilde{g}=\begin{cases} g\left(x\right) & x\neq a\\ 0 & x=a \end{cases} הגבול של מנתם בa יהיה זהה לגבול המקורי כי הוא נבדל ממנו רק בנקודה 1 לשם נוחות נמשיך לקרוא להם .f,g על פי משפט ערך הביניים של קושי עבור כל x בסביבה הימנית של a שבה f,g מוגדרות נוכל לבחור 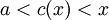a<c(x)<x שמקיימת 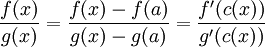\frac{f(x)}{g(x)}=\frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f'(c(x))}{g'(c(x))} ולכן נקבל 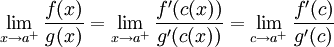\lim_{x\to a^{+}}\frac{f(x)}{g(x)}=\lim_{x\to a^{+}}\frac{f'(c(x))}{g'(c(x))}=\lim_{c\to a^{+}}\frac{f'(c)}{g'(c)} כרצוי השיוויון האחרון נובע מכך ש 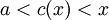a<c(x)<x וממשפט הסנדויץ

שימוש בכלל לופיטל

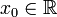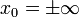תהיינה שתי פונקציות f,g. ותהי נקודה x_0\in\mathbb{R} או x_0=\pm\infty כך ש

\lim_{x\rightarrow x_0}f(x)=L
\lim_{x\rightarrow x_0}g(x)=M

נראה כיצד ניתן להעזר בכלל לופיטל על מנת לחשב גבולות במקרים בהם משפטי האריתמטיקה הרגילים נכשלים.

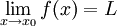
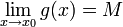
מקרה ראשון \frac{0}{0} או \frac{\infty}{\infty}

מקור: https://math-wiki.com/index.php?title=כלל_לופיטל&oldid=40415