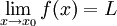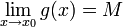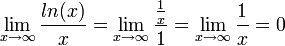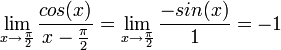כלל לופיטל
מתוך Math-Wiki
תוכן עניינים
משפט לופיטל
נניח כי 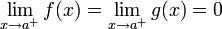 ונניח עוד כי
ונניח עוד כי 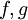 גזירות בסביבה ימנית של a ומתקיים
גזירות בסביבה ימנית של a ומתקיים 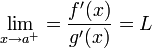 אז מתקיים
אז מתקיים 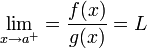
הוכחה
נוכל לבנות 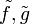 רציפות שמקיימות
רציפות שמקיימות 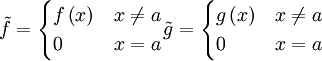 הגבול של מנתם בa יהיה זהה לגבול המקורי כי הוא נבדל ממנו רק בנקודה 1 לשם נוחות נמשיך לקרוא להם .f,g על פי משפט ערך הביניים של קושי עבור כל x בסביבה הימנית של a שבה f,g מוגדרות נוכל לבחור
הגבול של מנתם בa יהיה זהה לגבול המקורי כי הוא נבדל ממנו רק בנקודה 1 לשם נוחות נמשיך לקרוא להם .f,g על פי משפט ערך הביניים של קושי עבור כל x בסביבה הימנית של a שבה f,g מוגדרות נוכל לבחור 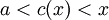 שמקיימת
שמקיימת 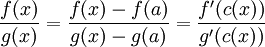 ולכן נקבל
ולכן נקבל 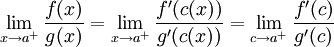 כרצוי השיוויון האחרון נובע מכך ש
כרצוי השיוויון האחרון נובע מכך ש 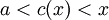 וממשפט הסנדויץ
וממשפט הסנדויץ
שימוש בכלל לופיטל
תהיינה שתי פונקציות f,g. ותהי נקודה 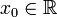 או
או 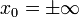 כך ש
כך ש
נראה כיצד ניתן להעזר בכלל לופיטל על מנת לחשב גבולות במקרים בהם משפטי האריתמטיקה הרגילים נכשלים.
מקרה ראשון  או
או 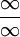
נניח 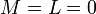 או
או 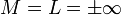
אזי אם הגבול 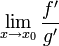 קיים, הוא שווה לגבול
קיים, הוא שווה לגבול 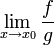
דוגמא 1
חשבו את הגבול 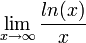 .
.
זהו מקרה של 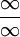 . נגזור את המונה והמכנה בנפרד ונקבל
. נגזור את המונה והמכנה בנפרד ונקבל
דוגמא 2
דוגמא 3
חשבו את הגבול 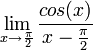 .
.
זהו מקרה של  . נגזור את המונה והמכנה בנפרד ונקבל
. נגזור את המונה והמכנה בנפרד ונקבל