גרסה מ־20:44, 19 באפריל 2012

תוכן עניינים

1 שאלה 1
2 שאלה 2
3 שאלה 3
4 שאלה 4
- 4.1 פתרון
5 שאלה 5
6 שאלה 6

שאלה 1

צטטו והוכיחו את משפט ליבניץ (או משפט ליפשיץ) על התכנסות טורים בעלי סימנים מתחלפים. אין צורך לצטט ולהוכיח את הטענה לגבי השארית.

שאלה 2

קבעו אם כל גבול קיים, ואם כן חשבו אותו.

א. 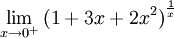$\lim_{x \to 0^{+}}{( 1+3x+2x^2 )}^{\frac{1}{x}}$

ב.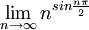 $\lim_{n \to \infty} n^{sin \frac{n \pi}{2}}$

שאלה 3

קבעו אם כל טור מתכנס או מתבדר:

א. $\sum_{n=3}^{\infty} \frac{1}{n \sqrt[3]{ln n}}$

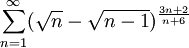
ב. $\sum_{n=1}^{\infty}( \sqrt{n} - \sqrt{n-1})^{\frac{3n+2}{n+6}}$

שאלה 4

א.

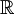הוכיחו שאם $f(x)$ מוגדרת ורציפה בכל $\mathbb{R}$ , אז עבור כל 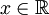$x \in \mathbb{R}$ מתקיים $\lim_{h \to 0} [f(x+h)-f(x-h)]=0$ .

ב.

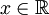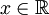הוכיחו שההיפך של סעיף א' אינו נכון. ז.א. יתכן שלכל $x \in \mathbb{R}$ מתקיים $\lim_{h \to 0} [f(x+h)-f(x-h)]=0$ ובכל זאת $f(x)$ אינה רציפה בכל $x \in \mathbb{R}$ .

פתרון

א.

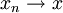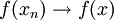לפי רציפות, ולפי הגדרת היינה לגבול, לכל סדרה $x_n\rightarrow x$ מתקיים $f(x_n)\rightarrow f(x)$ .

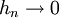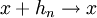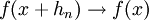לכן, לכל סדרה $h_n\rightarrow 0$ מתקיים $x+h_n\rightarrow x$ ולכן $f(x+h_n)\rightarrow f(x)$ . באופן דומה מקבלים 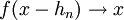$f(x-h_n)\rightarrow x$ וקיבלנו את הדרוש.

ב.

ניקח פונקציה קבועה למעט אי רציפות סליקה אחת. כיוון שהגבול קיים וסופי בכל נקודה, ההוכחה לעיל תקיפה פרט לשימוש בגבול במקום בערך בנקודה.

שאלה 5

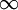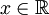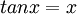הוכיחו שקיימים $\infty$ מספרים $x \in \mathbb{R}$ כך ש- $tan x= x$ .

שאלה 6

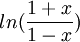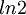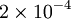השתמשו בפיתוח טיילור של הפונקציה $ln(\frac{1+x}{1-x})$ לחשב את $ln 2$ עם טעות קטנה מ- $2 \times 10^{-4}$ .

@@ שורה 17: / שורה 17: @@
 =שאלה 4=
-===סעיף א===
+א.
 הוכיחו שאם <math>f(x)</math> מוגדרת ורציפה בכל <math>\mathbb{R}</math>, אז עבור כל
 <math>x \in \mathbb{R}</math> מתקיים <math>\lim_{h \to 0} [f(x+h)-f(x-h)]=0</math>.
-'''פתרון.'''
+ב.
+הוכיחו שההיפך של סעיף א' אינו נכון. ז.א. יתכן שלכל <math>x \in \mathbb{R}</math> מתקיים
+<math>\lim_{h \to 0} [f(x+h)-f(x-h)]=0</math> ובכל זאת <math>f(x)</math> אינה רציפה בכל <math>x \in \mathbb{R}</math>.
+===פתרון===
+א.
 לפי רציפות, ולפי הגדרת היינה לגבול, לכל סדרה <math>x_n\rightarrow x</math> מתקיים <math>f(x_n)\rightarrow f(x)</math>.
 לכן, לכל סדרה <math>h_n\rightarrow 0</math> מתקיים <math>x+h_n\rightarrow x</math> ולכן <math>f(x+h_n)\rightarrow f(x)</math>. באופן דומה מקבלים <math>f(x-h_n)\rightarrow x</math> וקיבלנו את הדרוש.
-===סעיף ב===
+ב.
-הוכיחו שההיפך של סעיף א' אינו נכון. ז.א. יתכן שלכל <math>x \in \mathbb{R}</math> מתקיים
-<math>\lim_{h \to 0} [f(x+h)-f(x-h)]=0</math> ובכל זאת <math>f(x)</math> אינה רציפה בכל <math>x \in \mathbb{R}</math>.
+ניקח פונקציה קבועה למעט אי רציפות סליקה אחת. כיוון שהגבול קיים וסופי בכל נקודה, ההוכחה לעיל תקיפה פרט לשימוש בגבול במקום בערך בנקודה.
 =שאלה 5=

הבדלים בין גרסאות בדף "מבחן אינפי 1 סמסטר א' מועד ב' תשע"ב"

גרסה מ־20:44, 19 באפריל 2012

תוכן עניינים

שאלה 1

שאלה 2

שאלה 3

שאלה 4

פתרון

שאלה 5

שאלה 6

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים