הבדלים בין גרסאות בדף "מבחן השורש של קושי"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏מבחן השורש של קושי לטורים חיוביים)
(←‏הוכחה)
שורה 28: שורה 28:
  
 
ולכן הטור מתבדר.
 
ולכן הטור מתבדר.
 +
 +
 +
 +
כעת, נניח כי <math>\limsup \sqrt[n]{a_n} =d<1</math>.
 +
 +
*לכן החל ממקום מסויים בסדרה, <math>\sqrt[n]{a_n}<\frac{1-d}{2}<1</math>
 +
 +
*לכן <math>a_n<\Big(\frac{1-d}{2}\Big)^n</math>
 +
 +
*אבל <math>\sum \Big(\frac{1-d}{2}\Big)^n</math> הוא טור הנדסי מתכנס
 +
 +
*לכן לפי מבחן ההשוואה הראשון לטורים חיוביים, הטור שלנו מתכנס.
 +
 +
 +
 +
הטורים <math>\sum\frac{1}{n},\sum\frac{1}{n^2}</math> הם דוגמאות להתכנסות והתבדרות כאשר הגבול שווה ממש לאחד.

גרסה מ־09:49, 2 בפברואר 2012

חזרה למשפטים באינפי

מבחן השורש של קושי לטורים חיוביים

יהי 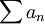\sum a_n טור חיובי. אזי:

אם \limsup \sqrt[n]{a_n} >1 הטור מתבדר
אם \limsup \sqrt[n]{a_n} <1 הטור מתכנס
אם \limsup \sqrt[n]{a_n} =1 לא ניתן לקבוע על פי מבחן זה.


הוכחה

נניח כי \limsup \sqrt[n]{a_n} =d>1. נבחר את תת הסדרה המתכנסת לגבול העליון:


\lim \sqrt[n_k]{a_{n_k}}=d
  • לכן החל ממקום מסויים בסדרה, \sqrt[n_k]{a_{n_k}}>\frac{d-1}{2}>1.
  • לכן a_{n_k}>\Big(\frac{d-1}{2}\Big)^{n_k}
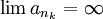
  • לכן \lim a_{n_k}=\infty
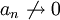
  • לכן בפרט a_n\not\rightarrow 0

ולכן הטור מתבדר.


כעת, נניח כי \limsup \sqrt[n]{a_n} =d<1.

  • לכן החל ממקום מסויים בסדרה, \sqrt[n]{a_n}<\frac{1-d}{2}<1
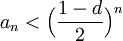
  • לכן a_n<\Big(\frac{1-d}{2}\Big)^n
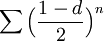  • אבל \sum \Big(\frac{1-d}{2}\Big)^n הוא טור הנדסי מתכנס
  • לכן לפי מבחן ההשוואה הראשון לטורים חיוביים, הטור שלנו מתכנס.


הטורים 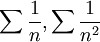\sum\frac{1}{n},\sum\frac{1}{n^2} הם דוגמאות להתכנסות והתבדרות כאשר הגבול שווה ממש לאחד.

מקור: https://math-wiki.com/index.php?title=מבחן_השורש_של_קושי&oldid=19257