הבדלים בין גרסאות בדף "מבחני התכנסות לאינטגרלים לא אמיתיים"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) מ |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 1: | שורה 1: | ||
==אינטגרלים לא-אמיתיים מסוג ראשון== | ==אינטגרלים לא-אמיתיים מסוג ראשון== | ||
===מבחן ההשוואה הראשון=== | ===מבחן ההשוואה הראשון=== | ||
| − | יהי <math>a\in\R</math>, ותהי נקודה <math>c\ge a</math> כך שמתקיים <math>\forall\ x\ge c:g(x)\ge f(x)\ | + | יהי <math>a\in\R</math> , ותהי נקודה <math>c\ge a</math> כך שמתקיים <math>\forall\ x\ge c:g(x)\ge f(x)\ge0</math> . |
אזי מתקיים: | אזי מתקיים: | ||
| − | <math>\int\limits_a^\infty g(x)dx</math> מתכנס <math>\displaystyle\int\limits_a^\infty f(x)dx\quad \Leftarrow\quad</math> מתכנס | + | <math>\int\limits_a^\infty g(x)dx</math> מתכנס <math>\displaystyle\int\limits_a^\infty f(x)dx\quad\Leftarrow\quad</math> מתכנס |
| − | <math>\int\limits_a^\infty f(x)dx</math> מתבדר <math>\displaystyle\int\limits_a^\infty g(x)dx\quad \Leftarrow\quad</math> מתבדר | + | <math>\int\limits_a^\infty f(x)dx</math> מתבדר <math>\displaystyle\int\limits_a^\infty g(x)dx\quad\Leftarrow\quad</math> מתבדר |
| − | <font size=4 color=#a7adcd> | + | <font size=4 color=#a7adcd>'''דוגמא'''</font> |
| − | '''דוגמא | + | |
| − | </font> | + | |
קבע האם <math>\displaystyle\int\limits_1^\infty\frac{\arctan(x)}{x}dx</math> מתכנס או מתבדר | קבע האם <math>\displaystyle\int\limits_1^\infty\frac{\arctan(x)}{x}dx</math> מתכנס או מתבדר | ||
| − | + | ;פתרון | |
נשים לב כי <math>\arctan(x)</math> היא פונקציה מונוטונית עולה ולכן בתחום האינטגרציה: | נשים לב כי <math>\arctan(x)</math> היא פונקציה מונוטונית עולה ולכן בתחום האינטגרציה: | ||
| − | <math>\forall\ x>1 : \arctan(x)>\arctan(1)=\frac{\pi}{4}>0</math> ולכן <math>\forall\ x>1:\frac{\arctan(x)}{x}>\frac{\pi}{4x}>0 </math> | + | <math>\forall\ x>1:\arctan(x)>\arctan(1)=\frac{\pi}{4}>0</math> ולכן <math>\forall\ x>1:\frac{\arctan(x)}{x}>\frac{\pi}{4x}>0 </math> |
| − | <math>\int\limits_1^\infty\frac{\pi}{4x}dx= \frac{\pi}{4}\int\limits_1^\infty\ | + | <math>\int\limits_1^\infty\frac{\pi}{4x}dx=\frac{\pi}{4}\int\limits_1^\infty\frac{dx}{x}</math> מתבדר, ולכן, עפ"י מבחן ההשוואה הראשון, האינטגרל שלנו גם כן מתבדר. |
===מבחן ההשוואה הגבולי=== | ===מבחן ההשוואה הגבולי=== | ||
| − | יהי <math>a\in\R</math>, ותהיינה שתי פונקציות <math>f(x),g(x)</math> כך ש: <math>\forall\ x\ge a:f(x),g(x)>0</math> | + | יהי <math>a\in\R</math> , ותהיינה שתי פונקציות <math>f(x),g(x)</math> כך ש: <math>\forall\ x\ge a:f(x),g(x)>0</math> |
| − | יהי הגבול | + | יהי הגבול <math>\lim\limits_{x\to\infty}\frac{f(x)}{g(x)}=L</math> |
| − | <math>\lim\limits_{x\to\infty}\frac{f(x)}{g(x)}=L</math> | + | |
'''אזי:''' | '''אזי:''' | ||
| − | אם <math>L>0 , L\in\R</math> אז <math>\displaystyle\int\limits_a^\infty f(x)dx</math> ו- <math>\displaystyle\int\limits_a^\infty g(x)dx</math> מתכנסים או מתבדרים יחדיו ("חברים"). | + | אם <math>L>0,L\in\R</math> אז <math>\displaystyle\int\limits_a^\infty f(x)dx</math> ו- <math>\displaystyle\int\limits_a^\infty g(x)dx</math> מתכנסים או מתבדרים יחדיו ("חברים"). |
אם <math>L=0</math> אז <math>\displaystyle\int\limits_a^\infty g(x)dx</math> מתכנס <math>\displaystyle\int\limits_a^\infty f(x)dx\quad \Leftarrow\quad</math> מתכנס. | אם <math>L=0</math> אז <math>\displaystyle\int\limits_a^\infty g(x)dx</math> מתכנס <math>\displaystyle\int\limits_a^\infty f(x)dx\quad \Leftarrow\quad</math> מתכנס. | ||
גרסה אחרונה מ־18:35, 12 בנובמבר 2016
תוכן עניינים
אינטגרלים לא-אמיתיים מסוג ראשון
מבחן ההשוואה הראשון
יהי 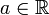 , ותהי נקודה
, ותהי נקודה 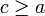 כך שמתקיים
כך שמתקיים 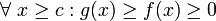 .
.
אזי מתקיים:
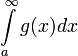 מתכנס
מתכנס 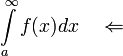 מתכנס
מתכנס
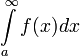 מתבדר
מתבדר 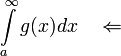 מתבדר
מתבדר
דוגמא
קבע האם 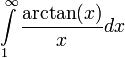 מתכנס או מתבדר
מתכנס או מתבדר
- פתרון
נשים לב כי 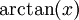 היא פונקציה מונוטונית עולה ולכן בתחום האינטגרציה:
היא פונקציה מונוטונית עולה ולכן בתחום האינטגרציה:
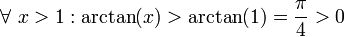 ולכן
ולכן 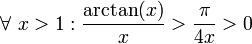
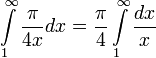 מתבדר, ולכן, עפ"י מבחן ההשוואה הראשון, האינטגרל שלנו גם כן מתבדר.
מתבדר, ולכן, עפ"י מבחן ההשוואה הראשון, האינטגרל שלנו גם כן מתבדר.
מבחן ההשוואה הגבולי
יהי 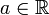 , ותהיינה שתי פונקציות
, ותהיינה שתי פונקציות 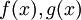 כך ש:
כך ש: 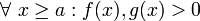
יהי הגבול 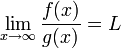
אזי:
אם 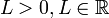 אז
אז 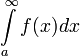 ו-
ו- 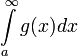 מתכנסים או מתבדרים יחדיו ("חברים").
מתכנסים או מתבדרים יחדיו ("חברים").
אם 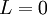 אז
אז 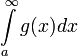 מתכנס
מתכנס 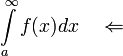 מתכנס.
מתכנס.
אם 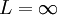 אז
אז 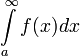 מתכנס
מתכנס 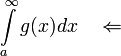 מתכנס.
מתכנס.