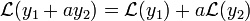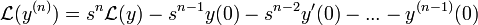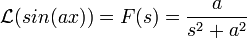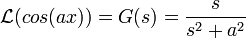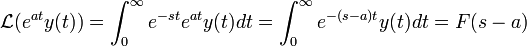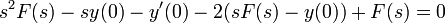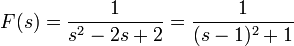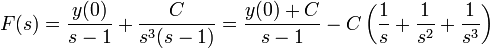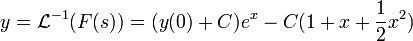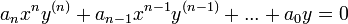מבחנים לדוגמא
- מבחן לדוגמא 1, פתרון
- מבחן לדוגמא 2, פתרון
- מבחן מועד א' תשע"ח, פתרון
- מבחן מועד ב' הנדסה תשע"ח, פתרון מבחן מועד ב' הנדסה תשע"ח
- מבחן מועד א' תשע"ט, פתרון
- מבחן מועד ב' תשע"ט, פתרון מבחן מועד ב' תשע"ט
- מבחן מועד א' תשפ"א, פתרון מבחן מועד א' תשפ"א
- מבחן מועד ב' תשפ"א, פתרון מבחן מועד ב' תשפ"א
- מבחן מועד א' תשפ"ב, פתרון מבחן מועד א' תשפ"ב
- מבחן מועד ב' תשפ"ב, פתרון מבחן מועד ב' תשפ"ב
- בוחן תשפ"ג, פתרון בוחן תשפ"ג
- מבחן מועד א' תשפ"ג, פתרון מבחן מועד א' תשפ"ג
- מבחן מועד ב' תשפ"ג, פתרון מבחן מועד ב' תשפ"ג
- בוחן הנדסה תשפ"ג, פתרון בוחן הנדסה תשפ"ג
- מבחן מועד א' הנדסה תשפ"ג, פתרון
- מבחן מועד ב' הנדסה תשפ"ג, פתרון
מבחנים של מד"ר למדעי המוח
הרצאות
פלייליסט של ההרצאות למחלקת מתמטיקה שנת תשפ"א
הרצאה 1 הקדמה ומשוואה פרידה
- משוואה דיפרנציאלית מכילה את המשתנה, הפונקציה ונגזרותיה.
- בחקירת פונקציות, במציאת תחומי עלייה וירידה, אנו פותרים את המשוואה
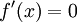 . האם זו משוואה דיפרנציאלית?
. האם זו משוואה דיפרנציאלית? - לא, כיוון שבמשוואות דיפרנציאלית אנו מחפשים פונקציה שמקיימת את המשוואה לכל ערך של המשתנה.
- כאן הפונקציה נתונה, ואנו מחפשים ערך של המשתנה שמקיים את המשוואה.
- המלצה: ניתן להעזר בספר המצויין על מד"ר של סמי זעפרני בקישור הבא.
נפילה חופשית
- גוף הנופל חופשית נופל בתאוצה שבקירוב היא קבועה
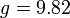 .
. - נסמן ב
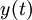 את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ)
את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ) 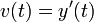 היא המהירות
היא המהירות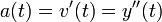 היא התאוצה.
היא התאוצה.- לכן על מנת לדעת את מיקומו של הגוף בכל נקודה בזמן, עלינו לפתור את המשוואה
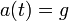 , הרי התאוצה קבועה.
, הרי התאוצה קבועה.
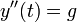
- לכן
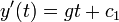
- לכן
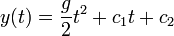
- כיצד נחשב את הקבועים? לפי תנאי ההתחלה.
- נסמן את הגובה ההתחלתי בתור 0 (נזכור כי הכיוון החיובי הוא לכיוון כדור הארץ). ולכן
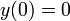 ולכן
ולכן 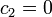
- נניח כי המהירות ההתחלתית גם היא הייתה 0 ולכן
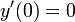 ולכן גם
ולכן גם 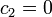 .
.
ריבית דריבית
- נניח שסכום הכסף בבנק לאורך זמן מתואר על ידי הפונקציה
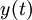 .
. - נניח שאנו מרוויחים תשואה של 2 אחוז בשנה, לכן לאחר שנה יתקיים כי
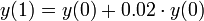 .
. - אבל מה היה קורה אילו הבנק היה משלם את הריבית פעם בחצי שנה?
- בחצי השנה הראשונה נקבל מחצית מהריבית

- ובחצי השנה השנייה נקבל מחצית מהריבית, אך סכום הקרן שלנו כבר גדל
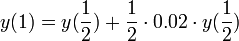
- סה"כ
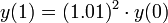
- בחצי השנה הראשונה נקבל מחצית מהריבית
- זה גדול יותר מהריבית השנתית, כיוון שצברנו ריבית על הקרן וגם על הריבית החצי שנתית.
- האם יש דרך להפוך את התהליך לרציף?
- כלומר, בהנתן שתי נקודות זמן קרובות אנו מעוניינים לקבל את הריבית היחסית על הזמן שעבר:
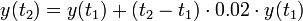
- נעביר אגף ונחלק
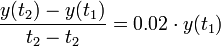
- אם נשאיף
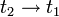 נקבל כי
נקבל כי 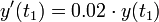
- כלומר אנו מעוניינים בפונקציה שמקיימת את המשוואה הדיפרנציאלית
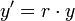 כאשר
כאשר 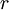 היא הריבית השנתית.
היא הריבית השנתית.
המשוואה 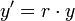
- בהמשך הקורס נעסוק בשאלה האם למשוואה דיפרנציאלית יש פתרון, וכמה פתרונות יש למשוואה.
- מידי פעם נחזור ונפתור את המשוואה הזו בכלים שונים.
- כעת נשים לב כי:
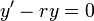
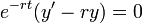
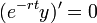
- כיוון שהנגזרת שווה אפס הפונקציה קבועה
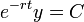
- סה"כ
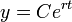
- על מנת לחשב את הקבוע C עבור המקרה של ריבית דריבית, עלינו לדעת כמה כסף היה בחשבון בזמן t=0.
- שימו לב שלכל תנאי התחלה קיבלנו פתרון יחיד.
סדר המד"ר
- משוואה דיפרנציאלית נקראת מסדר n אם הנגזרת הגבוהה ביותר היא מסדר n.
- המשוואה
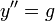 היא משוואה מסדר שני.
היא משוואה מסדר שני. - המשוואה
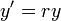 היא משוואה מסדר ראשון.
היא משוואה מסדר ראשון.
- המשוואה
משוואות פרידות
- משוואה דיפרנציאלית נקראת פרידה אם היא מהצורה
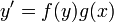 .
. - נהוג גם להחליף
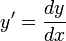 ולכן המשוואה תרשם כך
ולכן המשוואה תרשם כך 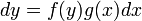 .
. - לבסוף, אם נזהר עם חלוקה באפס, משוואה פרידה באופן כללי יכולה להיות מהצורה
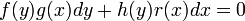 , כלומר
, כלומר 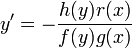 .
.
- משוואות פרידות אנו יכולים לפתור באמצעות אינטגרלים באופן הבא:
- ראשית נפריד (ומכאן השם) את המשתנים לשני צידי המשוואה:
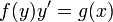
- הקדומות של שני הצדדים שוות עד כדי קבוע.
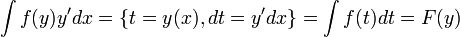
- לכן ביחד נקבל
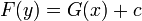
- בעצם אנו מחשבים אינטגרלים לשני הצדדים
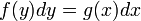 , כל אחד לפי המשתנה שלו!
, כל אחד לפי המשתנה שלו!
- לדוגמא נפתור את המשוואה
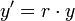 כמשוואה פרידה.
כמשוואה פרידה. - ראשית נפריד את המשתנים ונקבל כי
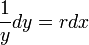 .
. - נשים לב כי הנחנו כאן כי
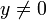 .
. - כעת
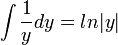 .
. 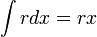 .
.- וביחד
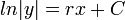 .
. - לכן
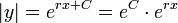 .
. - לכן
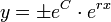 .
. - כעת, קל לראות מהצבה במשוואה כי y=0 גם פותר את המשוואה.
- בסה"כ הפתרון הכללי הוא (שוב)
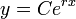 .
.
- שימו לב - חלקנו למקרים בהם הפונקציה שונה מאפס או קבועה אפס, אך לא טיפלנו במקרים בהם הפונקציה מידי פעם שווה אפס.
- בתרגיל זה איננו צריכים, כי מצאנו את הפתרון הכללי בדרך פשוטה יותר למעלה.
- בהמשך, משפט הקיום והיחידות יעזור לנו להתמודד עם השאלה הזו, אך באופן כללי לא נעסוק הרבה במקרי קצה בקורס זה.
המרדף
- דוגמא יפה וחשובה מהספר הזה עמוד 19 של הספר (33 של הPDF)
- מרצה צועד במהירות קבועה
 בקו ישר בשדרה שמוביל אל בניין 507.
בקו ישר בשדרה שמוביל אל בניין 507. - סטודנט שרוצה עוד שתי נקודות לעובר רואה את המרצה, ונע לכיוון המרצה במהירות קבועה
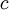 .
. - המרצה מתחיל בנקודה
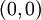 ונע בכיוון החיובי של ציר y, הסטודנט מתחיל בנקודה
ונע בכיוון החיובי של ציר y, הסטודנט מתחיל בנקודה 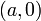 עבור
עבור 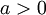 .
. - באיזה מסלול ינוע הסטודנט? באילו תנאים הוא יתפוס את המרצה?
- נסמן את פונקצית המסלול של הסטודנט ב
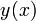
- כיוון שהסטודנט תמיד נע בכיוון המרצה, המשיק של הפונקציה בכל נקודה במסלול הסטודנט צריך לפגוש את המרצה באותו הזמן.
- בזמן
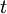 המרצה נמצא בנקודה
המרצה נמצא בנקודה 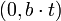 והסטודנט נמצא בנקודה
והסטודנט נמצא בנקודה 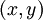 .
. - השיפוע בין המרצה לסטודנט הוא הנגזרת של פונקצית המסלול, כלומר
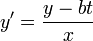
- כעת יש לנו שלושה משתנים
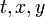 , כיצד נפטר מאחד מהם? לא השתמשנו במהירות הסטודנט!
, כיצד נפטר מאחד מהם? לא השתמשנו במהירות הסטודנט! - המסלול שהסטודנט עבר צריך להיות שווה ל
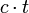 , כלומר
, כלומר 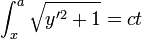
- מהמשוואה לעיל אנו יודעים כי
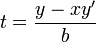
- ביחד נקבל כי
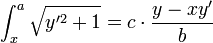
- נגזור את שני הצדדים ונקבל כי:
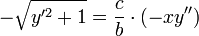
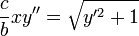
- נסמן
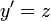 ונקבל
ונקבל 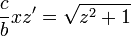
- זו מד"ר פרידה
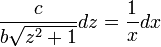
- באמצעות ההצבה האוניברסאלית המתאימה
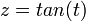 נפתור את האינטגרל של הצד השמאלי ונקבל כי
נפתור את האינטגרל של הצד השמאלי ונקבל כי 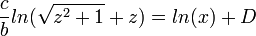
- ברגע הראשון התקיים כי
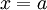 והתלמיד כיוון לראשית הצירים כלומר
והתלמיד כיוון לראשית הצירים כלומר 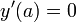 כלומר
כלומר 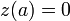
- לכן
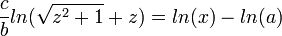
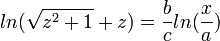
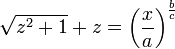
- כעת קצת אלגברה:
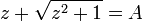
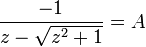
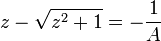
- נחבר למשוואה הראשונה
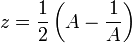
- הרי
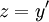 , ולכן ביחד:
, ולכן ביחד: 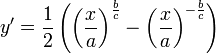
- ולכן אחרי אינטגרציה נקבל כי:
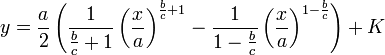
- כאשר אנחנו מקבלים את הקבוע
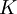 מהנתון
מהנתון 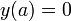
- באופן טבעי, אם מהירות המרצה גדולה ממהירות הסטודנט
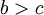 נקבל שאיפה לאינסוף כאשר
נקבל שאיפה לאינסוף כאשר 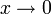 והסטודנט לא יגיע למרצה.
והסטודנט לא יגיע למרצה. - אם
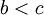 הסטודנט יגיע לשדירה ויתפוס את המרצה.
הסטודנט יגיע לשדירה ויתפוס את המרצה. - אם
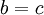 האינטגרציה שלנו שגוייה, וכאשר נחשב אותה נכון שוב נקבל שאיפה לאינסוף (באופן טבעי)
האינטגרציה שלנו שגוייה, וכאשר נחשב אותה נכון שוב נקבל שאיפה לאינסוף (באופן טבעי)
הפיכת משוואה לפרידה
- נביט במשוואה
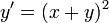 שאינה משוואה פרידה.
שאינה משוואה פרידה. - נדגים עכשיו טריק שיהפוך את המשוואה לפרידה.
- נגדיר את הפונקציה
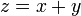 .
. - מתקיים כי
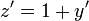 וביחד המשוואה המקורית מקבלת את הצורה
וביחד המשוואה המקורית מקבלת את הצורה 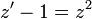 .
. - זוהי משוואה פרידה
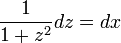 .
. - נפעיל אינטגרל על שני הצדדים ונקבל כי
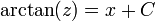
- ולכן
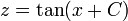
- ולכן

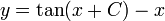
- שימו לב לדוגמא, כאן לא התייחסנו למקרה הקצה בו
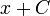 מחוץ לתחום
מחוץ לתחום 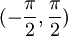 .
. - שיטה אחת לוודא שהפתרון שלנו אכן נכון היא להציב את התוצאה שקיבלנו ישירות במשוואה.
- על מנת לדעת אם לא פספסנו פתרונות אחרים, נעזר בהמשך במשפט הקיום והיחידות.
- אבל כאמור - אנחנו לא נתייחס באופן כזה לכל מקרה קצה בהמשך הקורס.
הרצאה 2 מד"ר הומוגנית, מד"ר לינאריות מסדר ראשון ומשוואת ברנולי
מד"ר הומוגנית
- מד"ר הומוגנית (בניגוד למד"ר לינארית הומוגנית שנראה בהמשך) היא משוואה מהצורה
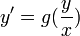 .
. - נפתור מד"ר הומוגנית באמצעות ההצבה
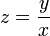 באופן הבא:
באופן הבא:
- ראשית נסמן
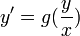 .
. - כעת נגזור את שני צידי המשוואה
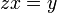 , ונקבל כי
, ונקבל כי 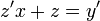 .
. - לכן לאחר החלפת המשתנה קיבלנו משוואה פרידה
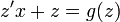 .
. - נפריד את המשתנים
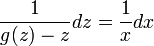 .
. - ולכן
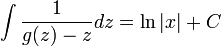 .
. - נמצא את
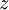 ונציב בחזרה
ונציב בחזרה 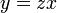 .
.
- ראשית נסמן
- פונקציה
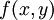 נקראת הומוגנית מסדר k אם לכל
נקראת הומוגנית מסדר k אם לכל 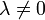 מתקיים כי
מתקיים כי 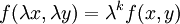 .
. - לדוגמא
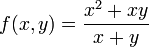 הומוגנית מסדר 1.
הומוגנית מסדר 1.
- טענה: פונקציה
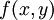 היא מהצורה
היא מהצורה 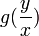 לכל
לכל 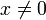 אם"ם היא הומוגנית מסדר
אם"ם היא הומוגנית מסדר 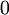 לכל
לכל 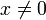 .
. - הוכחה:
- אם
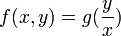 אזי לכל
אזי לכל 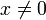 מתקיים
מתקיים 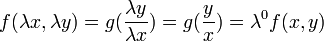 .
. - אם
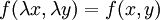 , נציב
, נציב 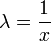 ונקבל כי
ונקבל כי 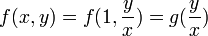 .
.
- אם
- דוגמא - נפתור את המשוואה
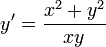
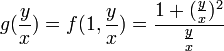
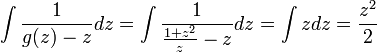
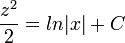
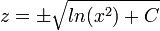
- ולבסוף
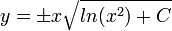
- דוגמא - נפתור את המשוואה
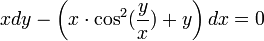
מד"ר לינארית מסדר ראשון
- הגדרה: משוואה מסדר ראשון נקראת לינארית אם היא מהצורה
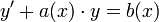 .
. - מד"ר לינארית הומוגנית (בניגוד למד"ר הומוגנית שראינו לעיל) היא מהצורה
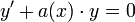 .
. - נחשב נוסחא לפתרון מד"ר לינארית כללית ע"י מציאת פתרון למשוואה לינארית הומוגנית ובאמצעות שיטת וריאצית המקדמים.
- נשים לב כי המשוואה הלינארית ההומוגנית
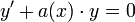 היא פרידה.
היא פרידה. - נפריד את המשתנים ונקבל
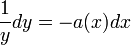 .
. - נבצע אינטגרציה ונקבל כי
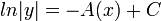 .
. - ולכן
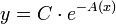
- כעת נשתמש בשיטת וריאצית המקדמים על מנת לפתור את המד"ר הלא הומוגנית.
- נציב במקום המקדם הקבוע
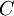 פונקציה
פונקציה 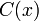 , וננחש שזה פתרון של המד"ר.
, וננחש שזה פתרון של המד"ר. - כיוון שאנו מנחשים שזה פתרון של המד"ר, נציב אותו בתוך המשוואה ונמצא (בתקווה) פונקציה
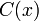 כך שהמשוואה תתקיים.
כך שהמשוואה תתקיים.
- כלומר, נציב
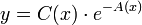 במשוואה
במשוואה 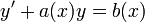 .
. - נקבל
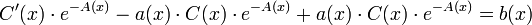
- משוואה זו מתקיימת אם"ם
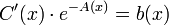 .
. - כלומר
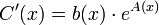 .
. - לכן נבחר
![C(x)=\int \left[b(x)\cdot e^{A(x)}\right]dx+C](/images/math/a/9/5/a95c5c07114e5f6c04cd2c6593b2c797.png)
- סה"כ הפתרון הכללי למד"ר הלינארית
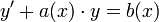 הוא:
הוא:
- דוגמא - המשוואה החביבה עלינו
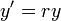 :
:
- ראשית, נשים לב כי
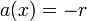 ו
ו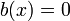 .
. - כלומר זו מד"ר לינארית הומוגנית, והפתרון הכללי הוא
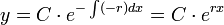
- ראשית, נשים לב כי
נפילה חופשית כולל התנגדות אוויר
- גוף בעל מסה
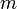 נמצא בנפילה חופשית, מצד אחד הוא מושפע מכוח הכבידה שנחשב קבוע
נמצא בנפילה חופשית, מצד אחד הוא מושפע מכוח הכבידה שנחשב קבוע 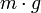 ומצד שני מכוח התנגדות האוויר.
ומצד שני מכוח התנגדות האוויר. - במהירויות גבוהות נניח שהוא פרופורציונלי למהירות הנפילה בריבוע
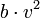 , ובמהירויות נמוכות נניח שהוא פרופורציונלי למהירות הנפילה
, ובמהירויות נמוכות נניח שהוא פרופורציונלי למהירות הנפילה 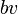 .
.
במהירות גבוהה
- לפי החוק השני של ניוטון
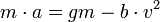 .
. - כלומר
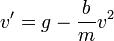
- נבצע הפרדת משתנים
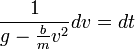
- נבצע פירוק לשברים חלקיים:
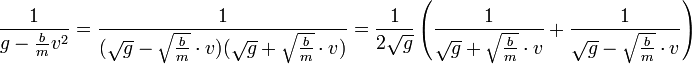
- ולכן
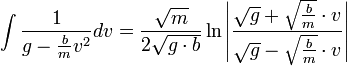
- מצד שני
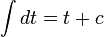
- לכן
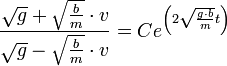
- נסדר קצת
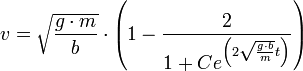
- נשים לב שכאשר
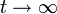 אנו מתכנסים למהירות הסופית
אנו מתכנסים למהירות הסופית 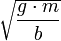 .
. - אם זו הייתה המהירות ההתחלתית היינו מקבלים פונקצית מהירות קבועה.
במהירות נמוכה
- לפי החוק השני של ניוטון
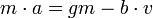 .
. - כלומר קיבלנו את המד"ר הלינארית
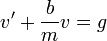 .
. - ולכן הפתרון הוא
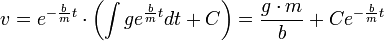 .
. - וכאשר
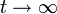 המהירות שואפת למהירות הסופית
המהירות שואפת למהירות הסופית 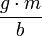 .
.
משוואת ברנולי
- משוואת ברנולי היא משוואה מהצורה
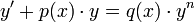 עבור
עבור 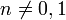 .
. - נפתור את המשוואה על ידי הצבה שתהפוך אותה למשוואה לינארית, אותה כבר למדנו לפתור.
- נניח כי
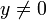 , ונחלק ב
, ונחלק ב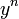 .
. - נקבל את המשוואה
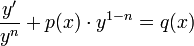 .
. - נציב
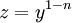 .
. - נגזור
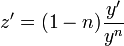 .
. - נקבל משוואה לינארית
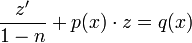 .
. - נפתור עבור
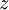 ונציב חזרה לקבל
ונציב חזרה לקבל 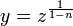 .
.
- דוגמא - נפתור את המשוואה
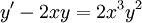 .
.
- נציב
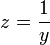 .
. - נקבל
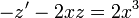 ולכן
ולכן 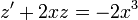 .
. - לכן
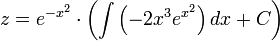
- לכן
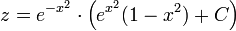
- לכן
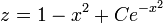
- ולבסוף
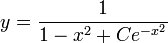
- נציב
- דוגמא - גוף בתנועה עם כוח גרר לא לינארי ביחס למהירות
- נתון גוף הנע חצי באוויר וחצי בתוך נוזל כלשהו. נניח כי החיכוך עם הנוזל פרופורציונלי למהירות, והחיכוך עם האוויר פרופורציונלי למהירות בריבוע.
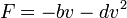 ולכן
ולכן 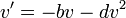 (לצורך הפשטות הכנסנו את המסה לתוך הקבועים).
(לצורך הפשטות הכנסנו את המסה לתוך הקבועים).- זוהי משוואת ברנולי, נציב
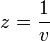 .
. - לכן
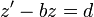
- נפתור את המשוואה הדיפרנציאלית:
- ולכן
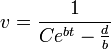
- כמובן שכאשר
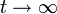 המהירות מתכנסת מהר מאד לאפס.
המהירות מתכנסת מהר מאד לאפס.
- דוגמא - המשוואה הלוגיסטית
- קצב הגדילה של אוכלוסיה פרופורציונלית לגודל האוכלוסיה כפול כמות המשאבים הפנויים.
- המשאבים קטנים באופן פרופורציונלי לגודל האוכלוסיה.
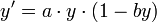
הרצאה 3 משוואות מדוייקות
הקדמה - פונקציות בשני משתנים
- נגזרות חלקיות
- דוגמא עבור
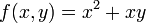 מתקיים
מתקיים 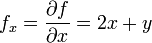 ו
ו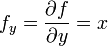
- דוגמא עבור
- עבור פונקציות דיפרנציאביליות (כמו הפונקציות האלמנטריות), מתקיים כי
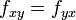 (כלומר סדר הנגזרות לא משנה).
(כלומר סדר הנגזרות לא משנה). - כלל השרשרת: אם
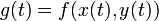 אזי
אזי 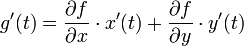
- בפרט, עבור
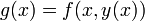 מתקיים
מתקיים 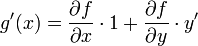
מד"ר מדוייקת
- מד"ר מסדר ראשון נקראת מדוייקת אם היא מהצורה
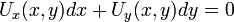 , עבור
, עבור 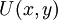 דיפרנציאבילית.
דיפרנציאבילית. - פתרון המד"ר ניתן בצורה סתומה על ידי המשוואה
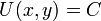 , כאשר C קבוע כלשהו.
, כאשר C קבוע כלשהו. - תהי מד"ר מהצורה
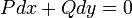 כאשר
כאשר 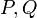 בעלות נגזרות רציפות. אזי המד"ר מדוייקת אם"ם
בעלות נגזרות רציפות. אזי המד"ר מדוייקת אם"ם 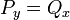
- הוכחה לפתרון המד"ר המדויקת:
- נגזור את הפונקציה
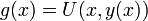 לפי המשתנה
לפי המשתנה 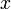 באמצעות כלל השרשרת ונקבל כי
באמצעות כלל השרשרת ונקבל כי 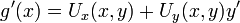
- לפי הנתון
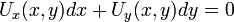 נובע כי
נובע כי 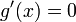 ולכן
ולכן 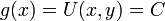 פונקציה קבועה.
פונקציה קבועה.
- נגזור את הפונקציה
- הוכחה לתנאי השקול למד"ר מדויקת:
- כיוון ראשון, נניח
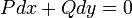 מדוייקת.
מדוייקת.
- לכן קיימת
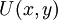 דיפרנציאבילית כך ש
דיפרנציאבילית כך ש 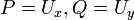 .
. - לכן
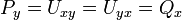 .
.
- לכן קיימת
- כיוון שני, נניח כי
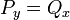 .
.
- אנו מחפשים
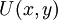 עבורה
עבורה 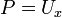 .
. - נעשה אינטגרציה לפי
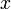 ונקבל כי
ונקבל כי 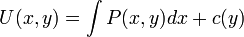 .
. - לכן ברור כי
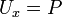 , השאלה היא אם ניתן לבחור
, השאלה היא אם ניתן לבחור 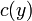 עבורו
עבורו 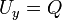 .
. - כלומר אנו רוצים
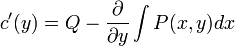
- משוואה זו תהיה פתירה, אם הצד הימני הוא פונקציה שאינה תלוייה בx.
- אכן
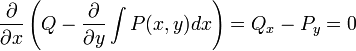 .
.
- אנו מחפשים
- כיוון ראשון, נניח
- דוגמא: מצאו משוואה המתארת את הפתרון למד"ר הבאה באופן סתום
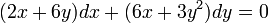 .
.
- ראשית נוודא שמדובר במשוואה מדוייקת:
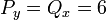 .
. - נבצע אינטגרציה
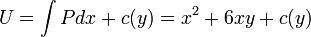 .
. - נגזור לפי y ונקבל כי
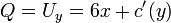 .
. - לכן
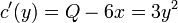 .
. - לכן
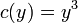 וסה"כ
וסה"כ 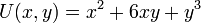 .
. - לכן הפתרון למד"ר נתון באופן סתום ע"י
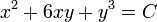 .
.
- ראשית נוודא שמדובר במשוואה מדוייקת:
גורם אינטגרציה
- לעיתים המד"ר אינה מדוייקת, אך ניתן לכפול אותה בפונקציה (שנקרא לה גורם אינטגרציה) וכך נהפוך אותה למדוייקת.
- באופן כללי אנו לא יודעים למצוא את גורם האינטגרציה, אבל נביט במקרה בו קיים גורם אינטגרציה שתלוי בx בלבד.
- תהי מד"ר
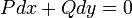 , ונניח שקיים לה גורם אינטגרציה
, ונניח שקיים לה גורם אינטגרציה 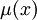 התלוי בx בלבד.
התלוי בx בלבד. - כלומר
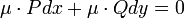 מדוייקת.
מדוייקת. - לכן
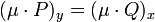 .
. - כלומר
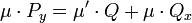 .
. - לכן
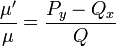 .
. - ניתן לפתור משוואה זו אם הצד הימני תלוי בx בלבד, כיוון שהצד השמאלי תלוי בx בלבד.
- במקרה זה, פתרון יהיה
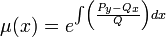
- דוגמא - המשוואה
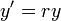 .
.
- המשוואה הינה
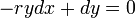 .
. 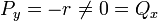
- מתקיים כי
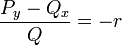 תלוי בx בלבד.
תלוי בx בלבד. - לכן יש גורם אינטגרציה
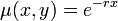
- נכפול את המשוואה בגורם האינטגרציה.
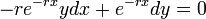 .
.- כעת
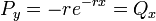 .
. 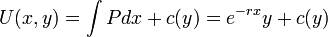
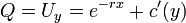 .
.- לכן
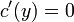 ואפשר לבחור
ואפשר לבחור 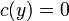 .
. - סה"כ
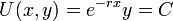 .
. - (כך פתרנו למעשה את משוואה זו בשיעור הראשון.)
- המשוואה הינה
- דוגמא - המשוואה
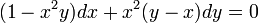 .
.
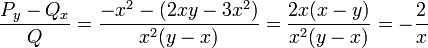
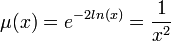 .
.- אכן המשוואה
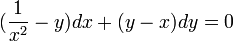 מדוייקת.
מדוייקת.
- נבדוק:
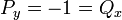 .
.
- נבדוק:
- נפתור את המד"ר:
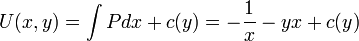 .
.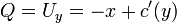 .
.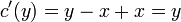 .
.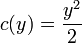 .
.- סה"כ הפתרון למד"ר נתון באופן סתום ע"י
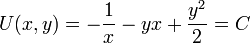 .
. - אפשר באמצעות השלמה לריבוע לבודד את y.
הרצאה 4 משפט הקיום והיחידות
בעיית קושי
- מציאת פתרון למד"ר
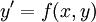 המקיימת
המקיימת 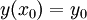
המשוואה האינטגרלית
- בעיית הקושי
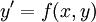 עם
עם 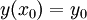 שקולה למשוואה
שקולה למשוואה 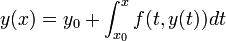 .
.
- בכיוון אחד - נניח כי המשוואה הדיפרנציאלית ותנאי ההתחלה נתונים.
- אזי
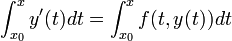 .
. - לכן
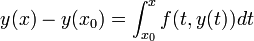 .
. - ולפי תנאי ההתחלה נקבל כי
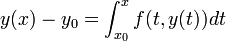 .
.
- אזי
- בכיוון שני, נניח כי המשוואה האינטגרלית נתונה.
- נגזור את שני הצדדים ונקבל את המשוואה הדיפרנציאלית (נגזרת של פונקצית שטח של פונקציה רציפה).
- נציב במשוואה האינטגרלית את
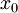 ונקבל
ונקבל 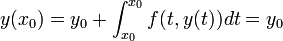 .
.
- בכיוון אחד - נניח כי המשוואה הדיפרנציאלית ותנאי ההתחלה נתונים.
שיטת פיקרד
- נראה את שיטת פיקרד, באמצעותה נוכיח את קיום הפתרון במשפט הקיום והיחידות.
- נבנה נוסחת נסיגה מהמשוואה האינטגרלית, ואז אם הסדרה תתכנס (במ"ש) נקבל את המשוואה האינטגרלית:
- נגדיר
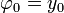 , ולכל
, ולכל  נגדיר
נגדיר 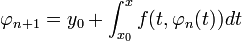 .
. - מאוחר יותר נוכיח כי סדרת הפונקציות מתכנסת לפתרון של המד"ר.
- דוגמא - נביט במשוואה (המאד מקורית)
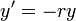 .
.
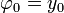
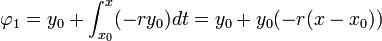
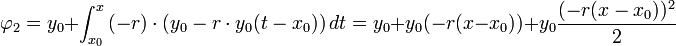
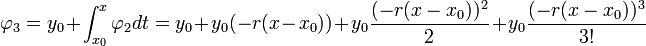
- נמשיך כך, ונקבל סדרת פונקציות המתכנסת ל
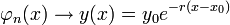
- אם נתון תנאי ההתחלה
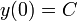 נקבל בדיוק את הפתרון
נקבל בדיוק את הפתרון 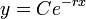 .
.
ניסוח משפט הקיום והיחידות
- תהי
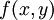 רציפה ובעלת נגזרת
רציפה ובעלת נגזרת 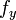 רציפה במלבן הסגור
רציפה במלבן הסגור 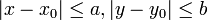 .
. - נביט בבעיית הקושי
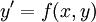 , עם תנאי ההתחלה
, עם תנאי ההתחלה 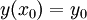
- נבחר
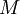 חסם כך ש
חסם כך ש 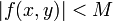 במלבן הנתון, ונסמן
במלבן הנתון, ונסמן 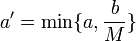 .
. - אזי קיים פתרון יחיד
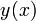 לבעיית הקושי בתחום
לבעיית הקושי בתחום 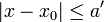 .
.
- הערות:
- שימו לב שהמשפט מבטיח פתרון בתחום מצומצם.
- אכן ראינו מד"ר שהייתה מוגדרת ורציפה בכל הממשיים, אך לא היה פתרון שמוגדר בכל הממשיים (
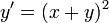 ).
). - לכל נקודה יש פתרון מסביבה, גם אם אין פתרון שמוגדר בכל מקום.
- אכן ראינו מד"ר שהייתה מוגדרת ורציפה בכל הממשיים, אך לא היה פתרון שמוגדר בכל הממשיים (
- שימו לב שאם מצאנו פתרון בצורה כלשהי, אנחנו יודעים שהוא יחיד בזכות המשפט (לפחות בסביבה מסויימת).
- מצד שני, אם הפתרון הכללי שמצאנו לא מקיים את תנאי ההתחלה, סימן שאנחנו צריכים לחפש פתרון שפספסנו.
הוכחת הקיום
- נוכיח שסדרת הפונקציות בשיטת פיקרד מתכנסת לפתרון לבעיית הקושי.
- הערה: נוכיח עבור
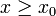 ההוכחות עבור
ההוכחות עבור 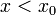 דומות.
דומות.
- ראשית, נוכיח שסדרת הפונקציות נשארת בתחום המלבן
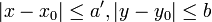 שנמצא בתוך המלבן המקורי ולכן מותר להשתמש בתכונות של
שנמצא בתוך המלבן המקורי ולכן מותר להשתמש בתכונות של 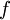 .
. - כלומר, עלינו להוכיח כי לכל
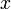 המקיים
המקיים 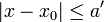 מתקיים כי
מתקיים כי 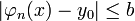 .
.
- הפונקציה הראשונה
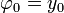 כמובן בתוך המלבן.
כמובן בתוך המלבן. - כעת יהי n עבורו הטענה נכונה, אזי
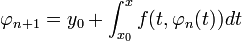 .
.
- שימו לב כי האינטגרל הוא בתחום
![[x_0,x]](/images/math/b/7/d/b7d76be1d097db06981b9ade286611e0.png) שנמצא בתחום התחום
שנמצא בתחום התחום ![[x_0,x_0+a']](/images/math/f/5/0/f50f868bebb3112f426e3e84e694b81d.png) .
.
- שימו לב כי האינטגרל הוא בתחום
- לכן
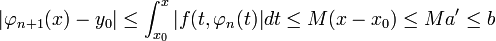 .
.
- הפונקציה הראשונה
- כעת, נשים לב לתכונה הבאה:
- כיוון ש
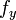 רציפה במלבן סגור היא חסומה נניח ע"י K.
רציפה במלבן סגור היא חסומה נניח ע"י K. - לפי משפט לגראנז' נקבל כי
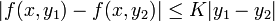
- כיוון ש
- כעת נוכיח שסדרת הפונקציות מתכנסת (במ"ש):
- ראשית, נשים לב כי
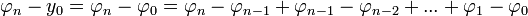 .
. - לכן עלינו להוכיח כי הטור
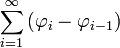 מתכנס במ"ש (כי הסס"ח שלו היא
מתכנס במ"ש (כי הסס"ח שלו היא 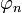 פחות קבוע).
פחות קבוע). - ראשית,
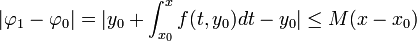
- כעת
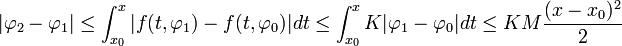
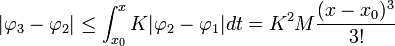
- נמשיך כך ונקבל כי
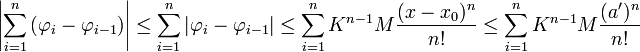
- זה טור מתכנס לפי מבחן המנה, וכן לפי מבחן הM של קושי הטור המקורי מתכנס במידה שווה.
- הערה: כיוון ש
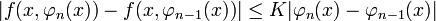 אזי גם הסדרה
אזי גם הסדרה 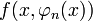 מתכנסת במ"ש באופן דומה.
מתכנסת במ"ש באופן דומה.
- ראשית, נשים לב כי
- נוכיח שפונקצית הגבול
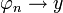 היא פתרון של בעיית הקושי.
היא פתרון של בעיית הקושי.
- נשאיף את שני צידי נוסחאת הנסיגה לאינסוף
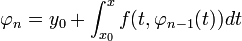 .
. - נקבל כי
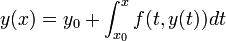 .
. - הערה: האינטגרל של הסדרה שואף לאינטגרל של פונקצית הגבול בזכות ההתכנסות במ"ש.
- נשאיף את שני צידי נוסחאת הנסיגה לאינסוף
הוכחת היחידות
- טענת עזר - תהי
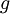 חסומה כך שלכל
חסומה כך שלכל 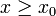 בקטע
בקטע 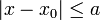 מתקיים כי
מתקיים כי 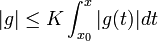 אזי
אזי 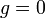 לכל
לכל 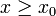 בקטע.
בקטע.
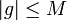 .
.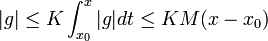 .
.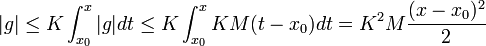 .
.- נמשיך כך ונקבל שלכל n מתקיים כי
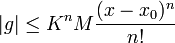 .
. - לכן
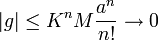 .
. - לכן
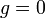 .
.
- יהיו שני פתרונות
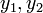 לבעיית הקושי, נוכיח כי
לבעיית הקושי, נוכיח כי 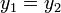 :
:
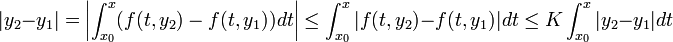 .
.- לכן לפי טענת העזר,
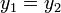 .
.
הרצאה 5 מד"ר מסדר גבוה (ובפרט סדר שני), מד"ר לינארית מסדר גבוה
- נחקור כעת משוואות מהצורה
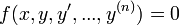
- דוגמא:
- נביט במסה המחוברת לקפיץ עם קבוע k, על משטח ללא חיכוך.
- נסמן את המרחק של המסה מהמצב הרפוי של הקפיץ בX.
- הכוח הפועל על המסה הוא
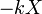 .
. - לכן לפי החוק השני של ניוטון
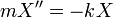 .
.
- דוגמא:
- נביט בסירה במים המחוברת בקפיץ למזח.
- מלבד הכוח שהקפיץ מפעיל, המים מתנגדים לסירה באופן פרופורציוני למהירות שלה.
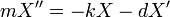
- היחס בין קבוע הקפיץ לקבוע התנגדות המים ישפיע על התנועה - האם הסירה תתקדם בכיוון אחד, או תעשה תנועה מחזורית (בכל מקרה היא תאט).
- דוגמא:
- מסה מחוברת לקפיץ עם חיכוך
- דוגמא:
- מסה תלוייה על קפיץ במאונך עם או בלי התנגדות אוויר ועם השפעת כוח המשיכה (לא הומוגני)
הורדת סדר המשוואה
מד"ר מסדר גבוה ללא y
- אם y אינו מופיע במשוואה פשוט נחליף משתנה
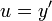 .
.
- דוגמא:
- משוואת נפילה חופשית ללא התנגדות אוויר היא מסדר שני
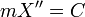 .
. - נביט בפונקצית המהירות
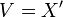 ונקבל את המשוואה
ונקבל את המשוואה 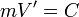 מסדר ראשון.
מסדר ראשון.
- משוואת נפילה חופשית ללא התנגדות אוויר היא מסדר שני
הורדת סדר למד"ר מסדר שני ללא x
- תהי מד"ר מהצורה
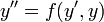 .
. - ראשית נחפש פונקציה
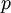 המקיימת את המד"ר מסדר ראשון
המקיימת את המד"ר מסדר ראשון 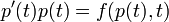
- נהוג לרשום את שם המשתנה כאן y ולא t, אך אני לא עושה את זה כעת על מנת למנוע בלבול מיותר.
- כעת נחפש פונקציה y המקיימת את המד"ר עבור p שמצאנו
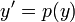
- פונקציה כזו תקיים כי
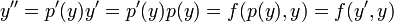
- כלומר היא מהווה פתרון למד"ר.
דוגמא - משוואות הקפיץ
- נחזור לדוגמא של מסה המחוברת לקפיץ, ולצורך הנוחות נחליף את פונקצית המיקום X בפונקציה y (המשתנה ישאר t).
- נניח כי המסה היא חלק מקבוע הקפיץ ונביט במשוואה
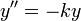 .
. - אנחנו רוצים למצוא p פונקציה של y המקיימת את המשוואה
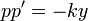 .
.
- זו משוואה פרידה
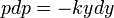 ולכן
ולכן 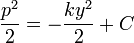 .
. - לכן
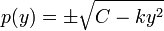 .
.
- זו משוואה פרידה
- לכן קיבלנו את המד"ר הפרידה
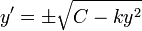 .
.
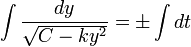 .
.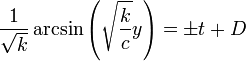 .
.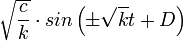 .
.- שימו לב שהביטוי
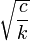 מייצג קבוע חיובי כלשהו.
מייצג קבוע חיובי כלשהו. - שימו לב שעבור בחירה מתאימה של הפאזה D גם cos הוא פתרון.
- שימו לב שישנם שני קבועים בפתרון. זה הגיוני, כי אנו צריכים שני תנאי התחלה - מיקום המסה, והמהירות שלה.
דוגמא - מהירות מילוט
- גוף בעל מסה
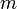 נזרק מכדור הארץ כלפי מעלה במהירות
נזרק מכדור הארץ כלפי מעלה במהירות 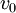 , נסמן את מרחק הגוף ממרכז כדור הארץ ב
, נסמן את מרחק הגוף ממרכז כדור הארץ ב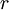 .
.
- מצאו את פונקצית מהירות הגוף ביחס לגובה שלו
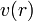 .
. - מהי מהירות המילוט של הגוף? כלומר עבור איזו מהירות התחלתית מתקיים כי
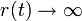 כאשר
כאשר 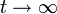 ?
?
- מצאו את פונקצית מהירות הגוף ביחס לגובה שלו
- נסמן את מסת כדור הארץ ב
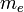 , את רדיוס כדור הארץ ב
, את רדיוס כדור הארץ ב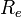 , את קבוע הכבידה האוניברסאלי ב
, את קבוע הכבידה האוניברסאלי ב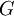 ואת תאוצת הנפילה בכדור הארץ ב
ואת תאוצת הנפילה בכדור הארץ ב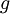
- ראשית נשים לב כי כוח המשיכה של כדור הארץ המופעל על מסה
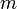 הוא בקירוב
הוא בקירוב 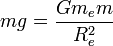 כלומר
כלומר 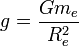 ולכן
ולכן 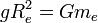
- המשוואה המתארת את תנועת הגוף היא:
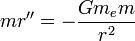 כלומר
כלומר 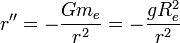
- זו משוואה מסדר שני שחסר בה המשתנה
- נחפש
 עבורה
עבורה 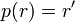 ולכן
ולכן 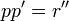
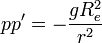
- נעשה אינטגרציה למד"ר הפרידה שקיבלנו ונקבל
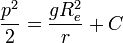
- לכן
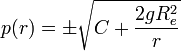
- ראשית נשים לב כי כוח המשיכה של כדור הארץ המופעל על מסה
- כיוון שהמהירות ההתחלתית היא חיובית נקבל כי
- על מנת למצוא את הקבוע, נציב את תנאי ההתחלה:
- הגובה הראשוני הוא
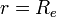 ובו המהירות היא
ובו המהירות היא 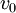
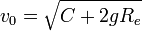
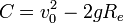
- הגובה הראשוני הוא
- הערה: ניתן לפתור את המד"ר הזו על מנת למצוא את הגובה כפונקציה של הזמן, אך לא התבקשנו לעשות כן.
- סה"כ נקבל כי
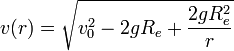
- מהירות המילוט היא המהירות ההתחלתית הנמוכה ביותר המבטיחה כי הגוף לא יגיע למהירות אפס.
- לכן מהירות המילוט מקיימת כי
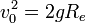 ולכן
ולכן 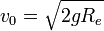
- לכל מהירות נמוכה יותר הביטוי בתוך השורש מתחיל מ
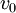 ושואף למספר שלילי (בהנחת השלילה ש
ושואף למספר שלילי (בהנחת השלילה ש 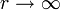 ), ולכן יגיע לאפס. במהירות אפס החפץ לא ימשיך לנוע.
), ולכן יגיע לאפס. במהירות אפס החפץ לא ימשיך לנוע. - לכל מהירות התחלתית גבוהה יותר, המהירות גדולה יותר מערך חיובי קבוע, ולכן
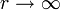 .
. - אם המהירות ההתחלתית היא בדיוק מהירות המילוט, ניתן לפתור את המד"ר בקלות ולראות כי
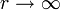 .
.
- לכל מהירות נמוכה יותר הביטוי בתוך השורש מתחיל מ
מד"ר לינארית
- מד"ר לינארית היא מד"ר מהצורה
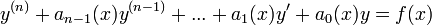 .
. - אם
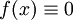 אזי המד"ר נקראת הומוגנית.
אזי המד"ר נקראת הומוגנית. - בעיית הקושי למד"ר הלינארית היא המשוואה יחד עם תנאי ההתחלה
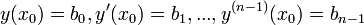
- משפט קיום ויחידות: אם
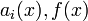 רציפות בקטע
רציפות בקטע 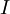 ויהי
ויהי 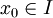 , אזי קיים פתרון יחיד בקטע
, אזי קיים פתרון יחיד בקטע 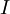 לבעיית הקושי.
לבעיית הקושי.
- נגדיר את אופרטור הגזירה
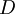 על מרחב הפונקציות הגזירות אינסוף פעמים.
על מרחב הפונקציות הגזירות אינסוף פעמים. 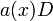 גם הוא אופרטור לינארי
גם הוא אופרטור לינארי- לכן ניתן לכתוב מד"ר לינארית כ
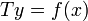 כאשר
כאשר 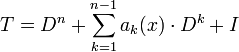 אופרטור לינארי.
אופרטור לינארי.
מד"ר לינארית הומוגנית
- אוסף הפתרונות של מד"ר לינארית הומוגנית הוא תת מרחב וקטורי.
- זה הרי הגרעין של האופרטור
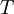 המתואר לעיל
המתואר לעיל
- זה הרי הגרעין של האופרטור
- תזכורת:
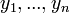 נקראת תלויות לינארית אם קיימים קבועים לא כולם אפס כך ש
נקראת תלויות לינארית אם קיימים קבועים לא כולם אפס כך ש 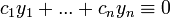 (הצירוף הוא פונקצית האפס).
(הצירוף הוא פונקצית האפס).
- הגדרה: הוורונסיקאן
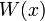 של הפונקציות
של הפונקציות 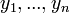 הוא הדטרמיננטה
הוא הדטרמיננטה 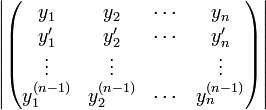
- אם
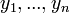 ת"ל אזי
ת"ל אזי 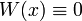 .
.
- נתון כי
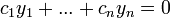
- נגזור
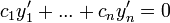
- נמשיך ולגזור ונקבל שלכל
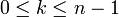 מתקיים כי
מתקיים כי 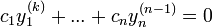 .
. - לכן
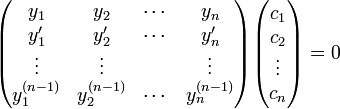
- כיוון שלמטריצה יש פתרון לא טריוואלי (ללא תלות בx) היא אינה הפיכה והדטרמיננטה שלה היא אפס.
- נתון כי
- אם
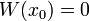 עבור
עבור 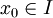 כלשהו עבור
כלשהו עבור 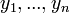 פתרונות של מד"ר לינארית הומוגנית עם מקדמים רציפים בקטע
פתרונות של מד"ר לינארית הומוגנית עם מקדמים רציפים בקטע 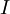 , אזי הפתרונות ת"ל ו
, אזי הפתרונות ת"ל ו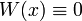 .
.
- כיוון ש
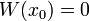 קיים פתרון לא טריוויאלי למערכת כך שלכל
קיים פתרון לא טריוויאלי למערכת כך שלכל 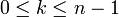 מתקיים כי
מתקיים כי 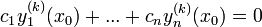 .
. - נביט בפונקציה
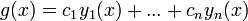 , לפי לינאריות גם
, לפי לינאריות גם 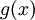 פתרון של המד"ר.
פתרון של המד"ר. - כיוון שלכל
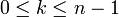 מתקיים כי
מתקיים כי 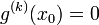 ולפי יחידות הפתרון, נובע כי
ולפי יחידות הפתרון, נובע כי 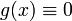 (הרי פונקצית האפס היא פתרון שמקיים את אותם תנאיי ההתחלה).
(הרי פונקצית האפס היא פתרון שמקיים את אותם תנאיי ההתחלה).
- כיוון ש
- הערה: ייתכנו פונקציות בת"ל שהוורונסיקאן שלהן מתאפס, אם הן לא פתרונות לאותו מד"ר לינארית. למשל
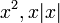 .
.
- דוגמא:
- נביט בוורונסקיאן של
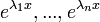 .
. 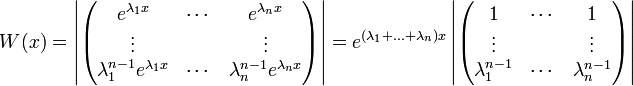
- זו מטריצת ונדרמונד ולכן
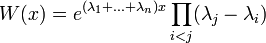
- לכן הפונקציות בת"ל אם ורק אם כל הקבועים שונים זה מזה
- נביט בוורונסקיאן של
- הוכחה לחישוב הדטרמיננטה של מטריצת ונדרמונד:
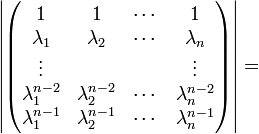
- נבצע את פעולות השורהעיבוד הנוסחה נכשל (שגיאת תחביר): R_n-\lambda_1 R_{n-1}\\R_{n-1}-\lambda_1 R_{n-2}\\\vdots\\R_2-\lambda_1 R_1
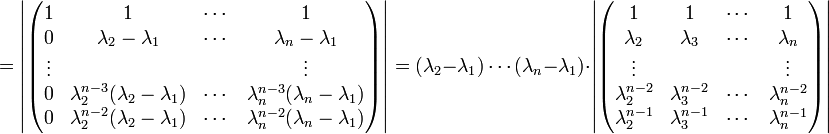
- כאשר המעבר הוא חישוב דטרמיננטה לפי העמודה הראשונה
- ומכאן סיימנו באינדוקציה
- מרחב הפתרונות של המד"ר הלינארית ההומוגנית הוא ממימד n.
- לכל
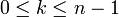 נגדיר את
נגדיר את 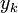 להיות הפתרון המקיים את תנאי ההתחלה
להיות הפתרון המקיים את תנאי ההתחלה 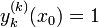 ואם
ואם 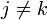 אז
אז 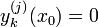 .
. - נוכיח שn פתרונות אלה מהווים בסיס.
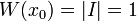 ולכן הפתרונות בת"ל.
ולכן הפתרונות בת"ל.- עבור תנאי ההתחלה
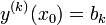 פתרון המקיים תנאיי התחלה אלו הוא
פתרון המקיים תנאיי התחלה אלו הוא 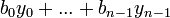 , ולכן הקבוצה פורשת.
, ולכן הקבוצה פורשת.
- לכל
- דוגמא: משוואת המסה על קפיץ
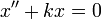
- נביט בפתרונות
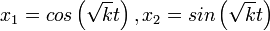 , הן אכן פותרות את המשוואה.
, הן אכן פותרות את המשוואה. - נביט בוורונסקיאן
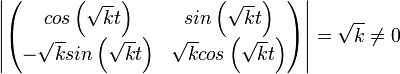
- לכן אלו שני פתרונות בת"ל שפורשים את כל מרחב הפתרונות, ולכן הפתרון הכללי הוא מהצורה
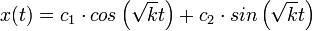
- נביט בפתרונות
מד"ר לינארית לא הומוגנית
- פתרון כללי למד"ר הלינארית שווה לפתרון הכללי למד"ר ההומוגנית ועוד פתרון פרטי למד"ר הלא הומוגנית
- הוכחה זהה לטיעון לגבי מערכות משוואות לינאריות.
- דוגמא:
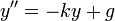 מסה התלוייה על קפיץ אנכי, עם השפעת כוח המשיכה. גובה אפס הוא הנקודה בה הקפיץ רפוי, הכיוון החיובי הוא למטה.
מסה התלוייה על קפיץ אנכי, עם השפעת כוח המשיכה. גובה אפס הוא הנקודה בה הקפיץ רפוי, הכיוון החיובי הוא למטה.
- נמצא פתרון פרטי ע"י ניחוש מושכל.
- נחפש פתרון מהצורה
 .
. - נציב ונקבל
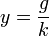 .
.
- לכן פתרון כללי למד"ר הוא
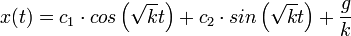 .
.
- דוגמא:
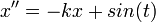 מסה על קפיץ עם כוח חיצוני שתלוי בזמן.
מסה על קפיץ עם כוח חיצוני שתלוי בזמן.
- נמצא פתרון פרטי ע"י ניחוש מושכל.
- נחפש פתרון מהצורה
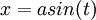 .
. 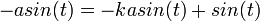 .
.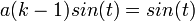 .
.- משוואה זו תתקיים עבור
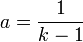 .
.
- לכן פתרון כללי למד"ר הוא
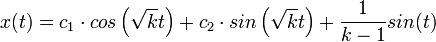 .
.
הרצאה 6 מד"ר לינארית עם מקדמים קבועים
ראשית נציג גישה אחת לנושא, ומאוחר יותר נציג גרסא מעודכנת (2022) המבוססות יותר על אופרטורים.
פולינום אופייני
- נביט במד"ר הלינארית ההומוגנית עם מקדמים קבועים
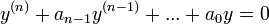 כאשר
כאשר 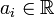 .
. - דוגמאות:
- משוואת הקפיץ
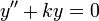 .
. 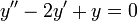 .
.
- משוואת הקפיץ
- ננחש פתרון למד"ר מהצורה
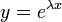 .
. - נציב במד"ר ונקבל
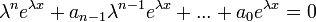 .
. - לכן
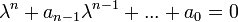 .
. - נגדיר את הפולינום האופייני של המד"ר להיות
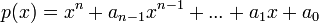 .
. - לכל שורש של הפולינום האופייני, קיבלנו פתרון למד"ר.
- דוגמא:
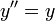
- נעביר אגף ונמצא את הפולינום האופייני:
- לכן השורשים של הפולינום האופייני הם
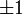 .
. - לכן שני פתרונות למד"ר הם
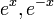 .
. - ראינו שהם בת"ל בעזרת הורונסקיאן ולכן הפתרון הכללי למד"ר ההומוגנית הוא
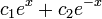 .
.
- נעביר אגף ונמצא את הפולינום האופייני:
- מה קורה כאשר חסרים שורשים (מרוכבים)?
- מה קורה כאשר שורש חוזר על עצמו?
- הפולינום האופייני של המד"ר
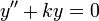 הוא
הוא 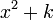 .
. - הפולינום האופייני של המד"ר
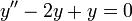 הוא
הוא  .
.
- כאשר השורש הוא מרוכב, נעזר באנליזה מרוכבת:
- ראשית, אם
 שורש של פולינום ממשי גם הצמוד שלו הוא שורש של הפולינום.
שורש של פולינום ממשי גם הצמוד שלו הוא שורש של הפולינום. - נזכר גם כי
- כעת, נניח שיש זוג שורשים מרוכבים
 לכן
לכן 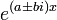 הן פתרונות.
הן פתרונות. - לכן גם צירוף לינארי שלהם הוא פתרון:
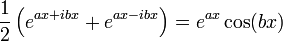
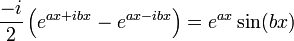
- עבור זוג השורשים המרוכבים הצמודים קיבלנו זוג פתרונות ממשיים בת"ל!
- ראשית, אם
- דוגמא משוואת הקפיץ
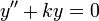 .
.
- הפולינום האופייני הינו
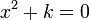 .
. - שורשי הפולינום האופייני הינם
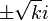 .
. - הפתרונות למד"ר ההומוגנית הם
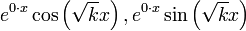 .
.
- הפולינום האופייני הינו
- כעת נטפל במקרה בו שורש חוזר על עצמו:
- ראשית, נביט באופרטור הלינארי
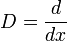 ששולח פונקציה לנגזרת שלה, ונסמן ב
ששולח פונקציה לנגזרת שלה, ונסמן ב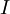 את אופרטור הזהות.
את אופרטור הזהות. - למשל המד"ר
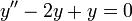 ניתנת להצגה כ
ניתנת להצגה כ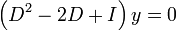 .
. - לכן
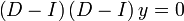 .
. - הפולינום האופייני של המד"ר הוא
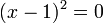 ולכן
ולכן 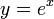 הוא פתרון.
הוא פתרון. - כעת, נראה כי גם
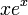 הוא פתרון של המד"ר.
הוא פתרון של המד"ר.
- באופן דומה אפשר להוכיח שאם ריבוי השורש הוא
 אזי לכל
אזי לכל 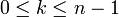 הביטוי
הביטוי 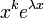 הוא פתרון.
הוא פתרון.
- ראשית, נביט באופרטור הלינארי
סיכום מציאת פתרון כללי למד"ר הומוגנית עם מקדמים קבועים
- מוצאים את הפולינום האופייני, ואת כל השורשים שלו (כולל המרוכבים).
- לכל שורש ממשי
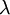 מריבוי
מריבוי  מתאימים הפתרונות
מתאימים הפתרונות 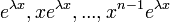 .
. - לכל שורש מרוכב
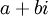 מריבוי
מריבוי  (ידוע שגם הצמוד שלו שורש מאותו ריבוי) מתאימים הפתרונות
(ידוע שגם הצמוד שלו שורש מאותו ריבוי) מתאימים הפתרונות 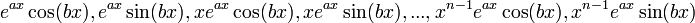
- סה"כ מצאנו למד"ר מסדר n בדיוק n פתרונות.
- הפתרונות הללו בת"ל ולכן הפתרון הכללי הוא צירוף לינארי שלהם.
- נוכיח שהפתרונות בת"ל (מעל המרוכבים).
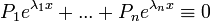 .
.- נניח ש
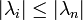 , נחלק ב
, נחלק ב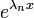 .
. - נציב
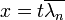 ונשאיף את
ונשאיף את 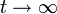 .
. - נקבל כי הפולינום המקדם של האקספוננט הגדול ביותר חייב להיות אפס.
- לכן באינדוקציה כל הפולינומים חייבים להיות אפס, ולכן כל אחד מהקבועים חייב להיות אפס.
- כיוון שהפתרונות בת"ל מעל המרוכבים, אפשר ליצור איתם כל תנאי התחלה, ולקבל פונקציות ממשיות שפותרות אותו.
- דוגמא: מצאו את הפתרון הכללי של המד"ר
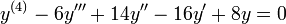 .
.
- ראשית, נמצא את הפולינום האופייני
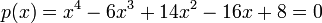 .
. - ננחש ש2 הוא שורש, נבצע חילוק, ננחש שוב את 2 כשורש ונקבל כי
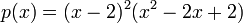 .
. - לכן השורשים של הפולינום האופייני הם 2 מריבוי 2, ו
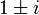 מריבוי 1.
מריבוי 1. - לכן הפתרון הכללי הוא
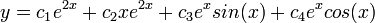 .
.
- ראשית, נמצא את הפולינום האופייני
- דוגמא: מצאו את הפתרון של המד"ר
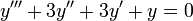 המקיים
המקיים 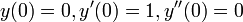 .
.
- הפולינום האופייני הוא
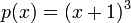 .
. - הפתרון הכללי הוא
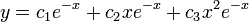 .
. - כעת נמצא את הקבועים:
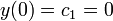 .
.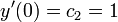 .
.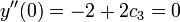 ולכן
ולכן 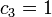 .
.
- סה"כ הפתרון הוא
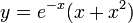 .
.
- הפולינום האופייני הוא
גישה מבוססת אופרטורים
- נציג את המד"ר הלינארית עם מקדמים קבועים באמצעות אופרטור הגזירה:
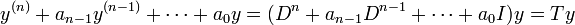
- נגדיר את הפולינום האופייני
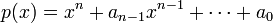
- סה"כ האופרטור של המד"ר הוא
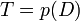
- נפרק את הפולינום האופייני לגורמים לינאריים מעל המרוכבים
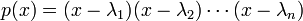
- ונקבל כי
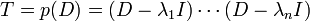
- שימו לב כי מותר לפתוח סוגריים באופן טבעי ואפשר להחליף בין סדר הגורמים כיוון ש
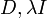 אופרטורים מתחלפים.
אופרטורים מתחלפים.
- שימו לב כי מותר לפתוח סוגריים באופן טבעי ואפשר להחליף בין סדר הגורמים כיוון ש
- כיוון שמותר להחליף את סדר הגורמים נובע כי אם
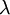 שורש של הפולינום האופייני מריבוי
שורש של הפולינום האופייני מריבוי 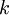 אזי
אזי
בטקסט לעיל, למדנו איך למצוא בסיס לגרעין הזה.
הרצאה 7 מציאת פתרון פרטי למד"ר לינארית לא הומוגנית
- כבר ראינו שעל מנת למצוא פתרון כללי למד"ר לינארית לא הומוגנית, עלינו למצוא פתרון כללי למד"ר ההומוגנית (למדנו כיצד בהרצאה קודמת), ופתרון פרטי כלשהו למד"ר הלא הומוגנית.
- נלמד כיצד למצוא פתרון פרטי.
שיטת הניחוש עבור מד"ר עם מקדמים קבועים
- תהי מד"ר מהצורה
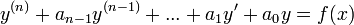 .
.
- אם
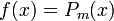 פולינום מדרגה m:
פולינום מדרגה m:
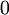 אינו שורש של הפולינום האופייני, ננחש
אינו שורש של הפולינום האופייני, ננחש 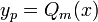 פולינום מדרגה m.
פולינום מדרגה m.- אם
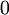 שורש של הפולינום האופייני מריבוי k ננחש
שורש של הפולינום האופייני מריבוי k ננחש  .
.
- אם
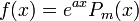 :
:
- אם
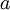 אינו שורש של הפולינום האופייני ננחש
אינו שורש של הפולינום האופייני ננחש 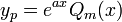 .
. - אם
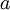 שורש של הפולינום האופייני מריבוי k ננחש
שורש של הפולינום האופייני מריבוי k ננחש 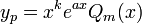 .
.
- אם
- אם
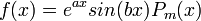 או
או 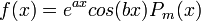 :
:
- אם
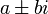 אינם שורשים של הפולינום האופייני ננחש
אינם שורשים של הפולינום האופייני ננחש  (כאשר
(כאשר 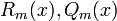 פולינומים מסדר m).
פולינומים מסדר m). - אם
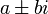 שורשים של הפולינום האופייני מריבוי k כל אחד, ננחש
שורשים של הפולינום האופייני מריבוי k כל אחד, ננחש 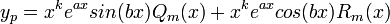 .
.
- אם
- דוגמאות:
- עבור
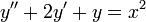 הפולינום האופייני הוא
הפולינום האופייני הוא 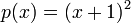 ננחש את הפתרון
ננחש את הפתרון 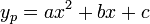 .
. - עבור
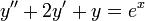 כעת
כעת 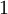 אינו שורש של הפולינום האופייני, ולכן ננחש
אינו שורש של הפולינום האופייני, ולכן ננחש 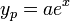 . (שימו לב שהפולינום הוא בעצם מדרגה 0.)
. (שימו לב שהפולינום הוא בעצם מדרגה 0.) - עבור
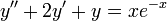 כעת
כעת 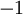 הוא שורש מריבוי 2 ולכן ננחש את הפתרון
הוא שורש מריבוי 2 ולכן ננחש את הפתרון 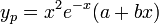 .
. - עבור
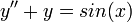 הפולינום האופייני הוא
הפולינום האופייני הוא 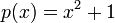 השורש
השורש 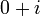 מופיע מריבוי 1 ולכן ננחש
מופיע מריבוי 1 ולכן ננחש 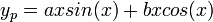 .
.
- עבור
- לאחר הניחוש, נמצא את הקבועים ע"י הצבה. נחשב עבור הדוגמא הראשונה:
- המד"ר
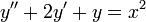 , הניחוש
, הניחוש 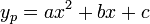 .
.
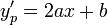 .
.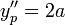 .
.- נציב
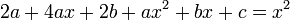 .
. - נבצע השוואת מקדמים:
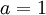 .
.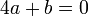 .
.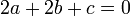 .
.
- לכן הפתרון הפרטי הוא
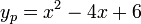 .
. - סה"כ הפתרון הכללי הוא
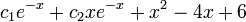 .
.
- המד"ר
וריאצית מקדמים יחד עם שיטת קרמר למד"ר לינארית
- תהי מד"ר לינארית (לאו דווקא עם מקדמים קבועים) מהצורה
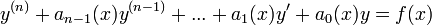 .
. - יהיו
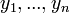 פתרונות בת"ל למד"ר ההומוגנית.
פתרונות בת"ל למד"ר ההומוגנית. - ננחש כי קיים פתרון פרטי מהצורה
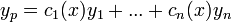 .
.
- טענה - עבור פונקציות
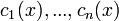 המקיימות את מערכת המשוואות
המקיימות את מערכת המשוואות
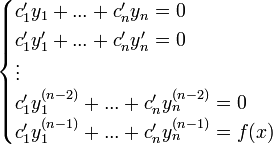
מתקיים כי 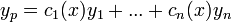 הוא פתרון פרטי של המד"ר.
הוא פתרון פרטי של המד"ר.
- הוכחה:
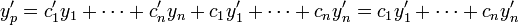 . (לפי המשוואה הראשונה.)
. (לפי המשוואה הראשונה.)- באופן דומה
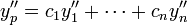 . (לפי המשוואה השנייה.)
. (לפי המשוואה השנייה.) - נמשיך כך עד שנקבל
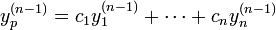
- כעת נגזור ונקבל
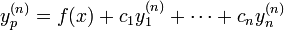 , לפי המשוואה האחרונה.
, לפי המשוואה האחרונה. - נציב במד"ר המקורית:
- כיוון ש
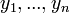 פתרונות למד"ר ההומוגנית הביטויים בסוגריים מתאפסים וסה"כ קיבלנו כי אכן
פתרונות למד"ר ההומוגנית הביטויים בסוגריים מתאפסים וסה"כ קיבלנו כי אכן 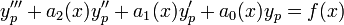 .
.
- נכתוב שוב את ההוכחה, בעזרת סימן הסכימה (עשוי להיות נוח יותר או פחות):
- ראשית, ניתן להוכיח באינדוקציה כי לכל
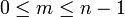 מתקיים כי
מתקיים כי 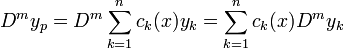
- כעת בעזרת המשוואה האחרונה נקבל כי
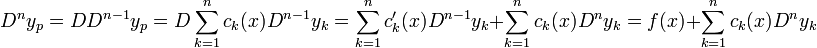
- נציב במד"ר ונקבל
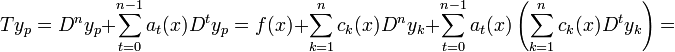
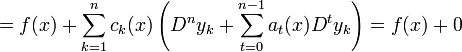
- ראשית, ניתן להוכיח באינדוקציה כי לכל
- כלומר, על מנת למצוא פתרון פרטי, עלינו למצוא פתרון למערכת המשוואות הבאה:
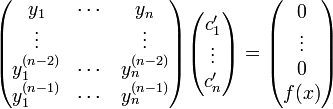
- אבל דטרמיננטת מטריצת המקדמים היא בדיוק הוורונסקיאן!
- כיוון ש
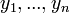 בסיס למרחב הפתרונות, מטריצת המקדמים הפיכה לכל
בסיס למרחב הפתרונות, מטריצת המקדמים הפיכה לכל  ולכן קיים פתרון (יחיד) למערכת.
ולכן קיים פתרון (יחיד) למערכת. - כיצד נמצא את הפתרון? שיטת קרמר.
- לאחר שנמצא את הערכים של
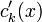 נבצע אינטגרציה ונמצא סה"כ את הפתרון הפרטי.
נבצע אינטגרציה ונמצא סה"כ את הפתרון הפרטי.
- דוגמא - מצאו פתרון כללי למד"ר
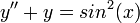 .
.
- פתרון כללי למד"ר ההומוגנית הוא
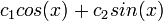 .
. - כעת עלינו למצא פתרון פרטי
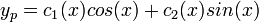 .
. - עלינו למצוא פתרון למערכת
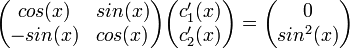
- לכן לפי שיטת קרמר
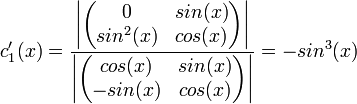
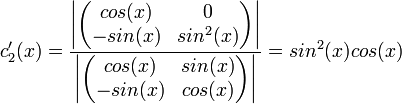
- לכן
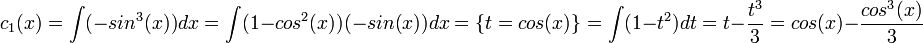
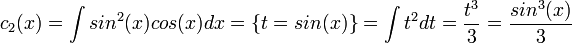
- סה"כ הפתרון הפרטי הוא
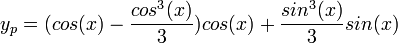 .
.
- פתרון כללי למד"ר ההומוגנית הוא
- דוגמא:
- שימו לב שיכלנו לפתור את השאלה הקודמת בדרך אחרת, קצרה יותר, עם טריק.
- מתקיים כי
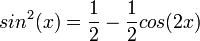 .
. - נמצא פתרון פרטי
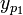 למד"ר
למד"ר 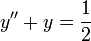 בשיטת הניחוש.
בשיטת הניחוש. - נמצא פתרון פרטי
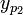 למד"ר
למד"ר 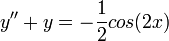 בשיטת הניחוש.
בשיטת הניחוש. - לכן
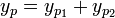 הוא פתרון פרטי למד"ר
הוא פתרון פרטי למד"ר 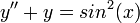 מתוך לינאריות.
מתוך לינאריות.
הרצאה 8 פתרון מד"ר באמצעות טורי טיילור
שימוש בטורי טיילור
- ננחש שהפתרון הוא טור חזקות, ואם אכן יש פתרון כזה, נמצא את המקדמים.
- גם אם לא נוכל למצוא נוסחא פשוטה לפונקציה, עדיין טור החזקות יכול לתת קירוב שלה.
- דוגמא: הזזת אינדקס של טור טיילור.
- הזיזו את האינדקס של הטור
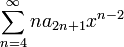 כך שהחזקה תהיה
כך שהחזקה תהיה 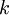 .
. - אנחנו רוצים להציב
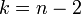 ולכן
ולכן 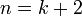 .
. - כיוון ש
 מתחיל מ4, נובע ש
מתחיל מ4, נובע ש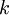 יתחיל מ2.
יתחיל מ2. - סה"כ נקבל כי
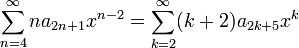 .
.
- הזיזו את האינדקס של הטור
- דוגמא מצאו את הפתרון הכללי למד"ר ההומוגנית
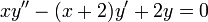 .
. - עבור
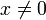 מדובר במד"ר לינארית הומוגנית בעלת שני פתרונות בת"ל.
מדובר במד"ר לינארית הומוגנית בעלת שני פתרונות בת"ל.
- ננחש כי קיים פתרון בצורת טור טיילור
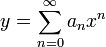 .
. - שימו לב שאנו מניחים שהפונקציה מוגדרת באפס, ייתכן שנרצה לפתח טור טיילור סביב נקודות אחרות באופן כללי.
- נציב במשוואה ונקבל:
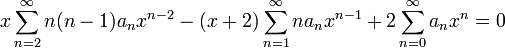
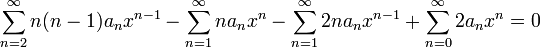
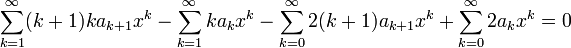
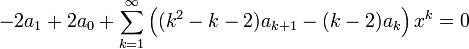
- לכן:
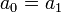
- לכל
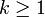 מתקיים
מתקיים 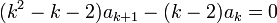 .
.
- עבור
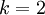 מקבלים
מקבלים 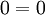 .
. - עבור
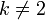 נחלק ב
נחלק ב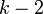 ונקבל
ונקבל 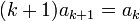 .
.
- עבור
- סה"כ המשוואות שקיבלנו הן
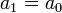
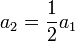
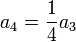
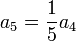
- וכן הלאה.
- נשים לב כי באופן כללי
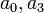 חופשיים.
חופשיים. - עבור הבחירה
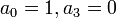 נקבל את הפתרון
נקבל את הפתרון 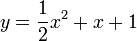 .
. - עבור הבחירה
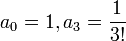 נקבל את הפתרון
נקבל את הפתרון 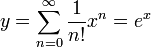 .
.
- נבדוק שהפתרונות בת"ל:
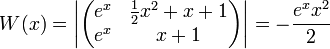
- לכל
 הוורונסיקאן שונה מאפס ולכן הפתרונות בת"ל.
הוורונסיקאן שונה מאפס ולכן הפתרונות בת"ל. - שימו לב שהוורונסיקאן התאפס בנקודה אחת, אבל זה בסדר כי המד"ר היא לינארית עבור
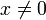 .
. - אכן ב
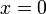 משפט היחידות לא עובד, שני הפתרונות מקיימים
משפט היחידות לא עובד, שני הפתרונות מקיימים 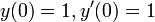 .
.
- סה"כ הפתרון הכללי הינו
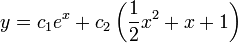
מציאת פתרון פרטי
- דוגמא - מצאו את הפתרון הכללי למד"ר
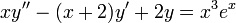 .
. - ראשית נעביר את המד"ר לצורה סטנדרטית
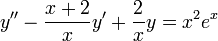
- נשתמש בשיטת וריאצית המקדמים על הפתרון למד"ר ההומוגנית יחד עם כלל קרמר.
- נחפש פתרון מהצורה
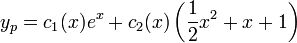 .
. - כעת
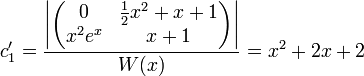
- לכן
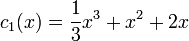 .
. - כמו כן,
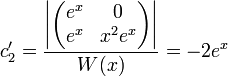
- לכן
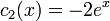 .
.
- נחפש פתרון מהצורה
- סה"כ הפתרון הפרטי הינו
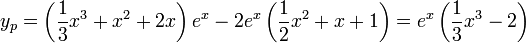
- לכן הפתרון הכללי הינו
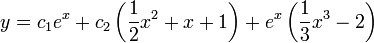
הרצאה 9 מערכות מד"ר
מערכת מד"ר לינארית מסדר ראשון עם מקדמים קבועים
- לעיתים יש לנו מד"ר העוסקות במספר פונקציות שונות.
- נניח שיש לנו סיר מים מתבשל על הגז.
- A היא מסת המים בסיר, וB היא מסת המים שהתאדו אל המכסה.
- נניח שקצב התאדות המים מהסיר אל המכסה הוא
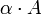 וקצב התעבות המים מהמכסה בחזרה לסיר הוא
וקצב התעבות המים מהמכסה בחזרה לסיר הוא 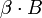 .
. - לכן
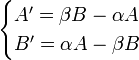
- נסמן את שתי הפונקציות ב
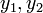 ונניח כי
ונניח כי 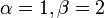 .
. - נקבל את המערכת
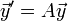 כלומר
כלומר 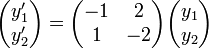
- נראה כיצד לכסון המטריצה A יעזור לנו לפתור את המערכת.
- במקרה בו A אינה לכסינה לא נטפל, אך אפשר לפתור אותו באופן כללי.
- עבור ו"ע מתקיים כי
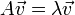 .
. - כיוון שהוקטור
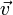 הוא וקטור קבועים,
הוא וקטור קבועים, 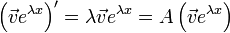 .
. - כלומר,
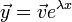 הוא פתרון למערכת.
הוא פתרון למערכת.
- בחזרה לדוגמא:
- הע"ע של
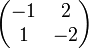 הם
הם 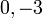 .
. - הו"ע המתאימים הם
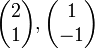
- הפתרון הכללי הוא
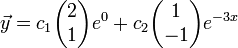
- כלומר
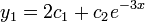 ו
ו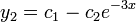
- הע"ע של
- שימו לב שככל שעובר הזמן היחס בין המים בסיר למים על המכסה שואף להיות קבוע.
- שימו לב ש
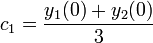 , זה הגיוני כיוון שמסת המים אינה משתנה בתהליך.
, זה הגיוני כיוון שמסת המים אינה משתנה בתהליך.
שתי מסות על קפיץ - מערכת מד"ר מסדר שני
- נביט בשתי מסות המחוברות לשני צידי קפיץ.
- נניח כי
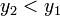 מודדות את מיקום המסות ביחס לנקודת האפס שלהן, וצד ימין הוא הכיוון החיובי בשתיהן.
מודדות את מיקום המסות ביחס לנקודת האפס שלהן, וצד ימין הוא הכיוון החיובי בשתיהן. - נניח כי כאשר כל אחת מהמסות במקום אפס, אזי הקפיץ במנוחה.
- נניח כי המסות זהות בגודלן, ושוות אחד.
- לכן מתקבלת מערכת המד"ר
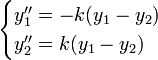
- שימו לב שכאשר הקפיץ מתוח הוא מושך את שתי המסות למרכז, כלומר את המסה הראשונה (הימנית) הוא מושך שמאלה (בכיוון השלילי), ואת המסה השנייה (השמאלית) הוא מושך ימינה (בכיוון החיובי)
- נסמן
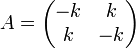 , ולכן
, ולכן 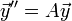 .
.
- הע"ע של A הינם
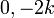 .
. - עבור הו"ע
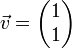 המתאים לע"ע
המתאים לע"ע 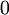 מתקיים כי
מתקיים כי 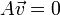 .
.
- לכן אם נבחר
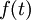 כך ש
כך ש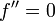 , ונבחר
, ונבחר 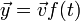 אזי נקבל
אזי נקבל 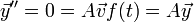 .
. - כלומר
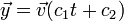 הוא פתרון למערכת.
הוא פתרון למערכת.
- לכן אם נבחר
- עבור הו"ע
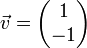 המתאים לע"ע
המתאים לע"ע 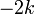 מתקיים כי
מתקיים כי 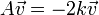 .
.
- לכן אם נבחר
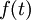 כך ש
כך ש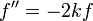 ונבחר
ונבחר 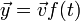 אזי נקבל
אזי נקבל 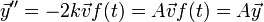 .
. - לכן
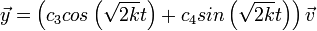 הוא פתרון למשוואה.
הוא פתרון למשוואה.
- לכן אם נבחר
- ביחד קיבלנו פתרון כללי
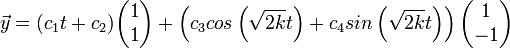
- תנאי ההתחלה הם המיקומים והמהירויות של כל אחת מהמסות.
קשר בין מד"ר מסדר גבוה למערכת מד"ר מסדר ראשון
- נביט במד"ר
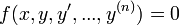 .
. - נסמן
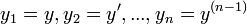 .
. - לכן המד"ר שקולה למערכת מסדר ראשון
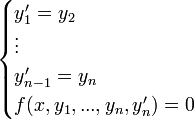 .
.
- בפרט, המד"ר הלינארית
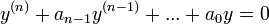 שקולה למערכת
שקולה למערכת 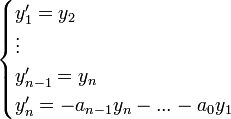
- בכתיב מטריצות קיבלנו את המערכת
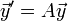 כאשר:
כאשר:
- הפולינום האופייני של
 הוא:
הוא:

- ניתן להוכיח באינדוקציה כי
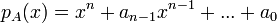 , בדיוק הפולינום האופייני של המד"ר המקורית, לא במפתיע.
, בדיוק הפולינום האופייני של המד"ר המקורית, לא במפתיע.
הרצאה 10 התמרת לפלס
- התמרת לפלס היא העתקה לינארית בין מרחבי פונקציות.
- עבור הפונקציה
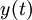 המוגדרת בקטע
המוגדרת בקטע 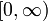 נגדיר את התמרת הלפלס
נגדיר את התמרת הלפלס 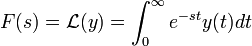 .
. - שימו לב שנהוג לסמן את הפונקציה לפני ההתמרה עם המשתנים x או t, ולאחר ההתמרה נהוג להתמש במשתנה s.
- אם מתקיים כי
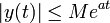 אזי ההתמרה מתכנסת לכל
אזי ההתמרה מתכנסת לכל 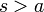 .
.
![\left|\int_0^\infty e^{-st}y(t)dt\right|\leq \int_0^\infty\left|e^{-st}y(t)\right|dt\leq \int_0^\infty Me^{(a-s)t}dt=\left[M\frac{e^{(a-s)t}}{a-s}\right]_0^\infty](/images/math/3/d/3/3d3c599d2ede1aa6403f3d6d8a9bb8a0.png)
- הביטוי האחרון מתכנס לכל
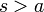 .
.
- נניח כי כל הפונקציות שאנו עוסקים בהן חסומות על ידי אקספוננט באופן דומה.
- דוגמא - נחשב את ההתמרה של הפונקציה
 .
.
- בויקיפדיה ניתן למצוא טבלה של התמרות לפלס שימושיות.
- שימו לב לשימוש בפונקצית המדרגה
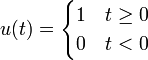 שמאפסת את כל החלק השלילי של ציר הx.
שמאפסת את כל החלק השלילי של ציר הx.
- הפונקציה
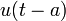 מאפסת את ציר הx בקטע
מאפסת את ציר הx בקטע 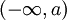 .
.
- הפונקציה
תכונות התמרת לפלס
- יחידות:
- אם
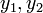 רציפות, ו
רציפות, ו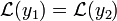 אזי
אזי 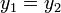 .
. - הוכחה
- אם
- לינאריות:
- התמרת הנגזרת הראשונה:
- התמרת נגזרת כללית:
- הזזה של המשתנה s:
- אם
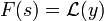 אזי
אזי 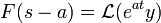
- אם
- הזזה של המשתנה t:
- אם
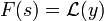 אזי
אזי 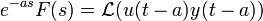
- אם
- תכונות נוספות:
- אם
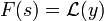 אזי
אזי 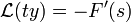
- אם
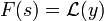 אזי
אזי 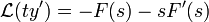
- אם
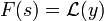 אזי
אזי 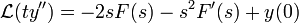
- אם
- נוכיח חלק מהתכונות לעיל כעת ובהרצאה הבאה.
- נוכיח עבור y החסומה ע"י אקספוננט כי
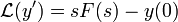
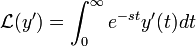
- נבצע אינטגרציה בחלקים
![\int_0^\infty e^{-st}y'(t)dt=\left[e^{-st}y(t)\right]_0^\infty+s\int_0^\infty e^{-st}y(t)dt = -y(0)+sF(s)](/images/math/d/6/5/d65a06fd18c4af6f615d6e143fa6e7f4.png)
- כעת
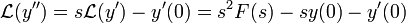 .
. - וכן הלאה, עבור נגזרות מסדר גבוה.
דוגמאות
- דוגמא - נמצא את ההתמרה של האקספוננט
- נציב בנוסחא
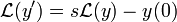 את
את 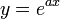
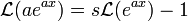
- סה"כ נקבל כי
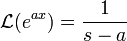
- דוגמא - נמצא פתרון למד"ר
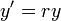 .
. - נבצע התמרת לפלס:
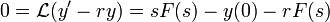
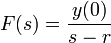
- לכן
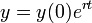
- דוגמא - נמצא את ההתמרה של סינוס וקוסינוס
- נסמן
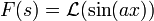 ,
, 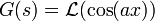
- נציב בנוסחא
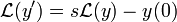 :
:
- נציב
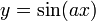 ונקבל
ונקבל 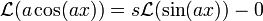 כלומר
כלומר 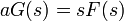
- נציב
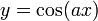 ונקבל
ונקבל 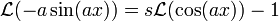 כלומר
כלומר 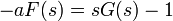
- נציב
- נקבל סה"כ כי
הרצאה 11 - המשך התמרת לפלס
- נוכיח כי
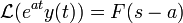
- נפתור את המד"ר
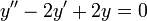 עם תנאי ההתחלה
עם תנאי ההתחלה 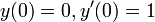 .
. - שימו לב שכבר למדנו איך לפתור מד"ר זו - למצוא פתרון כללי ולהציב תנאי ההתחלה.
- התמרת לפלס עשוייה לחסוך לנו קצת זמן.
- נבצע התמרת לפלס:
- ידוע ש
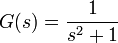 הינה ההתמרה של
הינה ההתמרה של 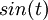 .
. - לכן
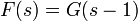 הינה ההתמרה של
הינה ההתמרה של 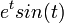 , וזהו פתרון המד"ר.
, וזהו פתרון המד"ר.
- נוכיח כי אם
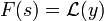 אזי
אזי 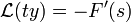
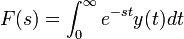 .
.- נגזור את שני הצדדים לפי
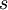 ונקבל כי
ונקבל כי
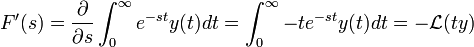
- את העובדה שגזרנו בתוך האינטגרל לא נצדיק כאן, היא נכונה עבור פונקציות שחסומות על ידי אקספוננט.
- לכן,
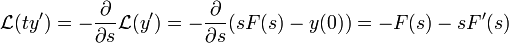
- כמו כן,
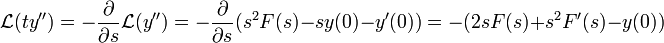
- דוגמא - נחשב את
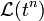 .
.
- ידוע כי
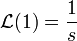
- לכן
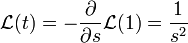
- לכן
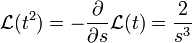
- לכן
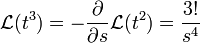
- ובאופן כללי
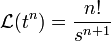
- ידוע כי
דוגמא
- נפתור את המד"ר
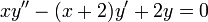 .
. - נבצע התמרת לפלס:
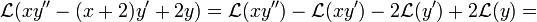
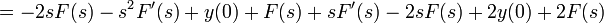
- לכן קבלנו את המשוואה
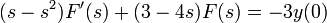
- קיבלנו מד"ר לינארית.
- לצורך הנוחות, נחליף זמנית את הסימון ונפתור את
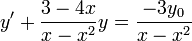
- נסמן
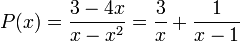 , ו
, ו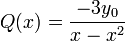
- לכן
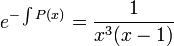 .
. - כמו כן
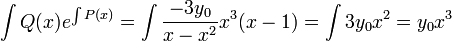
- סה"כ הפתרון למד"ר הלינארית הוא
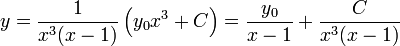
- נסמן
- נחזור לסימון התמרת הלפלס:
- נבצע התמרה הפוכה על מנת לקבל את הפתרון למשוואה המקורית:
דוגמא
- נמצא פתרון למד"ר
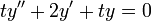 המקיים
המקיים 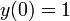 .
.
- נבצע התמרת לפלס
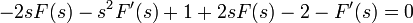 .
. - לכן
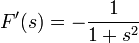
- לכן
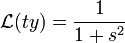
- לכן
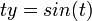
- לכן
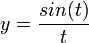
- נבצע התמרת לפלס
- הערות:
- הפונקציה שקיבלנו רציפה אם נגדיר אותה ב0 להיות 1, ואכן מקיימת את תנאי ההתחלה.
- מצאנו רק פתרון אחד, כיוון שלפתרון השני
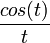 אין התמרת לפלס (האינטגרל לא מתכנס באיזור 0).
אין התמרת לפלס (האינטגרל לא מתכנס באיזור 0).
הרצאה 12 - הדלתא של דירק
הדלתא של דירק
- נתחיל ונאמר כי ישנן מספר גישות אל הדלתא של דירק, אנחנו נציג גישה אחת שרלוונטית אלינו.
- הדלתא של דירק אינה פונקציה, אלא מייצגת תהליך.
- למרות האמור, אנחנו נתייחס לתוצאה הסופית של התהליך, כאילו היה מדובר בפונקציה ממש.
- מטרה עיקרית: 'פונקצית הדלתא' מקיימת את התכונה
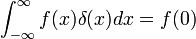 לכל פונקציה
לכל פונקציה 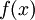 הרציפה ב
הרציפה ב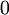 .
. - כמו כן,
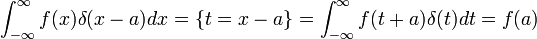 לכל פונקציה הרציפה בa.
לכל פונקציה הרציפה בa.
- בצורה מדוייקת יותר, נביט בסדרת הפונקציות
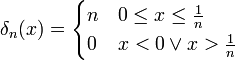
- כאשר
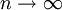 לכל
לכל 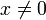 מתקיים כי
מתקיים כי 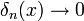 ועבור
ועבור 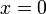 מקבלים כי
מקבלים כי 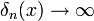 .
. - לכל
 מתקיים כי
מתקיים כי 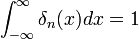 .
. - עקרונית הסדרה מייצגת פונקציות בעלות שטח אחד, ההולך ומתרכז בנקודה אפס.
- עבור
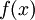 הרציפה בסביבה של
הרציפה בסביבה של  מתקיים כי:
מתקיים כי:
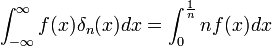
- לפי משפט ערך הממוצע האינטגרלי
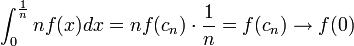
- נגדיר את
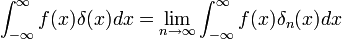
- נשים לב כי לפי גישה זו
 ו
ו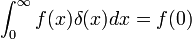 .
.
- נחשב את התמרת הלפלס של הדלתא של דירק:
- לכל
 מתקיים
מתקיים 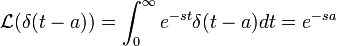
- בפרט
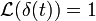
תגובת הלם
- נביט במערכת של מסה המחוברת לקפיץ, המתחילה במנוחה.
- נניח שברגע
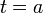 מישהו נתן 'פליק' למסה.
מישהו נתן 'פליק' למסה. - הדרך שלנו לבטא כוח נקודתי שכזה היא הדלתא של דירק, המכונה גם 'פונקצית הלם'.
- כלומר הכוח החיצוני על המערכת הוא
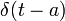 , בנוסף לכוח המופעל על ידי הקפיץ.
, בנוסף לכוח המופעל על ידי הקפיץ. - למעשה אנו מעוניינים בפתרון למד"ר
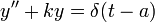
- באופן דומה להגדרת האינטגרל, ניתן לחשוב על הפתרון כגבול הפתרונות למערכות המקורבות
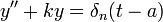 .
. - על מנת שיהיה פתרון למד"ר עלינו לבחור הפעם סדרה של פונקציות גזירות ב
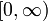 כמו
כמו 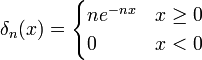
- נוכיח כעת את הנוסחא
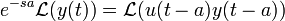 עבור
עבור 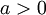 :
:
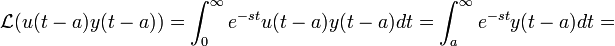
- נבצע את ההצבה
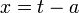 ונקבל:
ונקבל: 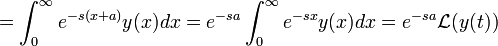 .
.
- נפתור את המערכת עם התמרת לפלס:
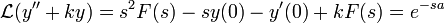 .
.- כיוון שהמערכת התחילה במנוחה,
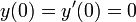 .
. - לכן
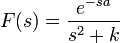 .
. - ולכן
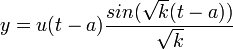 .
. - (הרי
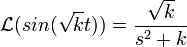 ).
).
- אכן, עד רגע
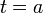 המערכת במנוחה
המערכת במנוחה 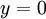 .
. - לאחר מכן, אנו מקבלים את הפתרון המקיים
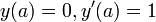 .
. - כלומר ה'הלם' תפקד במקרה זה כמו תנאי התחלה על המהירות - זה בדיוק ה'פליק' שהכנו במסה.
- נפתור את המערכת
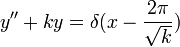 עם תנאי ההתחלה
עם תנאי ההתחלה 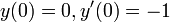 .
.
- נפעיל התמרת לפלס
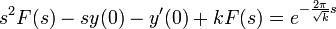
- לכן
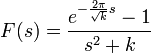
- לכן
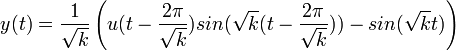
- לכן
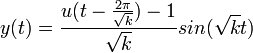
- כלומר בזמן
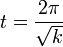 ההלם עוצר את התנועה במערכת, והפתרון מתאפס.
ההלם עוצר את התנועה במערכת, והפתרון מתאפס.
- נפעיל התמרת לפלס
- דוגמא - נפתור את המד"ר
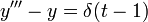 עבור תנאי ההתחלה
עבור תנאי ההתחלה 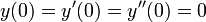 .
.
- נבצע התמרת לפלס ונקבל כי
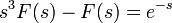 .
. - לכן
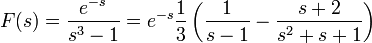
- ראשית נמצא את ההתמרה ההפוכה
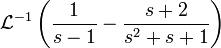 :
:
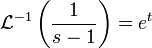
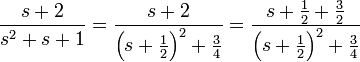
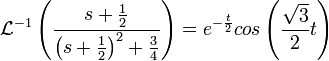
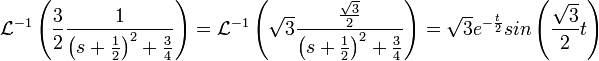
- לכן
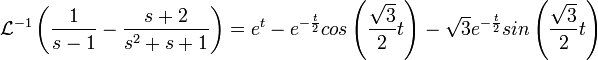
- ולכן סה"כ הפתרון למד"ר הינו
![y=\frac{u(t-1)}{3}\left[
e^{t-1}-e^{-\frac{t-1}{2}}cos\left(\frac{\sqrt{3}}{2}(t-1)\right)-
\sqrt{3}e^{-\frac{t-1}{2}}sin\left(\frac{\sqrt{3}}{2}(t-1)\right)
\right]](/images/math/c/f/c/cfc3bae0cbee45415af682b3785ca7d7.png)
- נבצע התמרת לפלס ונקבל כי
הרצאה 13 - משוואת אוילר
- משוואת אוילר הומוגנית היא משוואה מהצורה:
- נסמן את פונקצית האקפוננט
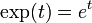
- נפתור את המד"ר ל
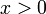
- נגדיר
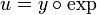 כלומר
כלומר 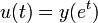 .
. - נקבל כי
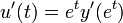
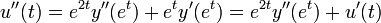
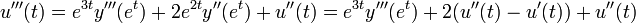
- באופן כללי ניתן להוכיח באינדוקציה כי
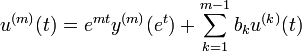 עבור קבועים כלשהם.
עבור קבועים כלשהם.
- נסמן את האופרטור המתאים למד"ר:
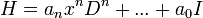
- לכן
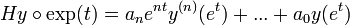
- לפי הפיתוח לעיל, זה שווה ל
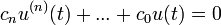 עבור קבועים כלשהם.
עבור קבועים כלשהם.
- נסמן את האופרטור המתאים למד"ר זו ב
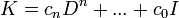
- סה"כ הוכחנו כי
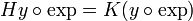
- סה"כ הוכחנו כי
- את הגרעין של
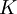 אנחנו יודעים למצוא כיוון שזו מד"ר לינארית הומוגנית עם מקדמים קבועים.
אנחנו יודעים למצוא כיוון שזו מד"ר לינארית הומוגנית עם מקדמים קבועים. - אם
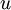 פתרון למד"ר המתאים ל
פתרון למד"ר המתאים ל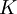 אז עבור
אז עבור 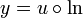 מתקיים כי
מתקיים כי 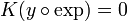
- לכן
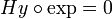 ולכן
ולכן 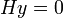 בחיוביים, שהרי זו התמונה של
בחיוביים, שהרי זו התמונה של 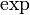 .
.
- אבל איך נמצא את הפתרונות ל
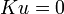 ? צריך למצוא את הפולינום האופייני.
? צריך למצוא את הפולינום האופייני. - עבור
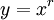 נקבל כי
נקבל כי 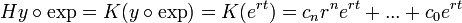
- אם נחלק ב
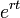 נקבל את הפולינום האופייני של המד"ר
נקבל את הפולינום האופייני של המד"ר 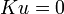 , זו נקראת המשוואה האינדנציאלית של משוואת האוילר המקורית.
, זו נקראת המשוואה האינדנציאלית של משוואת האוילר המקורית. - במילים פשוטות, על מנת לחשב את המשוואה האינדנציאלית:
- נציב
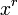 במשוואת האוילר
במשוואת האוילר - נציב
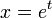 ונחלק ב
ונחלק ב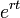 (או בעצם נחלק מראש ב
(או בעצם נחלק מראש ב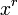 שזה שקול)
שזה שקול)
- נציב
- השורשים של המשוואה האינדנציאלית נותנים לנו את הפתרונות לגרעין של
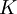 , נרכיב אותם על
, נרכיב אותם על 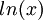 ונקבל את הפתרונות למשוואת האוילר.
ונקבל את הפתרונות למשוואת האוילר.
- סה"כ אם r שורש ממשי מריבוי k של המשוואה האינדנציאלית אזי:
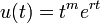 פתרון של המד"ר
פתרון של המד"ר 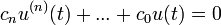 לכל
לכל 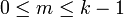 .
.- ולכן
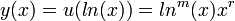 פתרון של משוואת אוילר המקורית, לכל
פתרון של משוואת אוילר המקורית, לכל 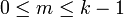 .
.
- אם
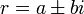 זוג שורשים מרוכבים צמודים מריבוי k כל אחד אזי:
זוג שורשים מרוכבים צמודים מריבוי k כל אחד אזי:
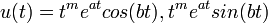 פתרונות של המד"ר
פתרונות של המד"ר 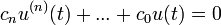 , לכל
, לכל 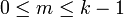 .
.- לכן
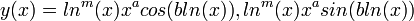 פתרונות של משוואת אוילר המקורית, לכל
פתרונות של משוואת אוילר המקורית, לכל 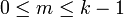 .
.
- דוגמא:
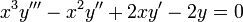
- נציב
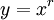 ונקבל את המשוואה האינדנציאלית
ונקבל את המשוואה האינדנציאלית 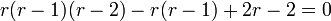 .
. - לכן
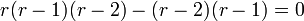 .
. - כלומר
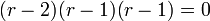 .
. - לכן הפתרון הכללי הינו
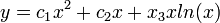
- דוגמא:
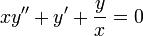
- נעביר לצורה של משוואת אוילר
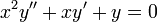 .
. - המשוואה האינדנציאלית היא
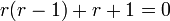 .
. - כלומר
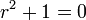 .
. - לכן הפתרון הכללי הינו
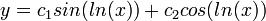
- דוגמא:
- מצאו פתרון כלשהו למד"ר
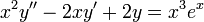
- ראשית נמצא את הפתרונות למד"ר ההומוגנית, שהיא משוואת אוילר.
- לאחר מכן נמצא פתרון פרטי באמצעות וריאצית המקדמים.
- מצאו פתרון כלשהו למד"ר
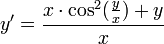
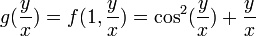
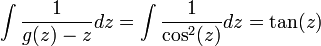
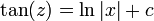
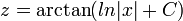
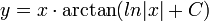
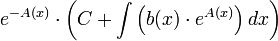
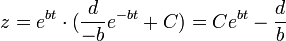
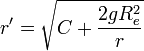
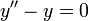
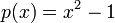
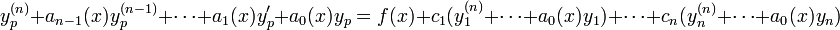
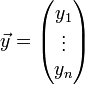
![\mathcal{L}(1)=\int_0^\infty e^{-st}dt = \left[\frac{e^{-st}}{-s}\right]_0^\infty = \frac{1}{s}](/images/math/0/d/5/0d5b86df2fe4fe2619a73fc3c0880199.png)