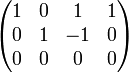הבדלים בין גרסאות בדף "מרחבי המטריצה"
יהודה שמחה (שיחה | תרומות) |
|||
| שורה 1: | שורה 1: | ||
[[קטגוריה:אלגברה לינארית]] | [[קטגוריה:אלגברה לינארית]] | ||
| − | תהי מטריצה <math>A\in\ | + | תהי מטריצה <math>A\in\Bbb{F}^{m\times n}</math> . מגדירים שלושה מרחבים עיקריים: |
| − | *'''מרחב השורות''' של A. זהו המרחב הנפרש על ידי שורות המטריצה | + | *'''מרחב השורות''' של <math>A</math> . זהו המרחב הנפרש על ידי שורות המטריצה. נסמן <math>R(A)=\text{span}\{R_1(A),\ldots,R_m(A)\}\sube\Bbb{F}^n</math> |
| − | *'''מרחב העמודות''' של A. זהו המרחב הנפרש על ידי עמודות המטריצה | + | *'''מרחב העמודות''' של <math>A</math> . זהו המרחב הנפרש על ידי עמודות המטריצה. נסמן <math>C(A)=\text{span}\{C_1(A),\ldots,C_n(A)\}\sube\Bbb{F}^m</math> |
| − | *'''מרחב האפס''' של A. זהו מרחב הפתרונות של המערכת ההומוגנית Ax=0. נסמן <math>N(A)=\{x\in\ | + | *'''מרחב האפס''' של <math>A</math> . זהו מרחב הפתרונות של המערכת ההומוגנית <math>Ax=0</math> . נסמן <math>N(A)=\{x\in\Bbb{F}^n|Ax=0\}\sube\Bbb{F}^n</math> |
| + | הגדרה: '''דרגת''' המטריצה <math>A</math> שווה למספר השורות בצורה המדורגת שלה השונות מאפס. מסומן <math>\text{rank}A</math> . | ||
| − | + | משפט: <math>\text{rank}A=\dim R(A)=\dim C(A)=n-\dim N(A)</math> . אלה שווים למספר המשתנים התלויים, וממד מרחב האפס שווה למספר המשתנים החופשיים. | |
| − | |||
| + | '''דוגמא.''' מצא בסיס למרחב האפס של המטריצה <math>\begin{pmatrix}1&0&1&1\\2&1&1&2\\1&1&0&1\end{pmatrix}</math> | ||
| − | + | ראשית, נדרג קנונית את המטריצה לקבלת | |
| − | + | :<math>\begin{pmatrix}1&0&1&1\\0&1&-1&0\\0&0&0&0\end{pmatrix}</math> | |
| − | + | לפיכך המשתנה השלישי והרביעי הם חופשיים, נציב במקומם פרמטרים <math>t,s</math> והפתרון הכללי הוא מהצורה <math>(-t-s,t,t,s)</math> . תמיד ניתן לפרק את הפתרון הכללי לסכום של וקטורים קבועים כפול הסקלרים שהם הפרמטרים: <math>t(-1,1,1,0)+s(-1,0,0,1)</math> . וקטורים קבועים אלה תמיד מהווים בסיס למרחב הפתרונות: | |
| − | + | *אנו רואים שכל פתרון הוא צירוף לינארי של הוקטורים הללו עם הסקלרים שהם הפרמטרים (במקרה זה <math>t,s</math>) | |
| − | + | ||
| − | <math>\begin{pmatrix}1 & 0 & 1 & 1\\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0\end{pmatrix}</math> | + | |
| − | + | ||
| − | לפיכך המשתנה השלישי והרביעי הם חופשיים, נציב במקומם פרמטרים t,s והפתרון הכללי הוא מהצורה <math>(-t-s,t,t,s)</math>. תמיד ניתן לפרק את הפתרון הכללי לסכום של וקטורים קבועים כפול הסקלרים שהם הפרמטרים: <math>t(-1,1,1,0) +s(-1,0,0,1)</math>. וקטורים קבועים אלה תמיד מהווים בסיס למרחב הפתרונות: | + | |
| − | *אנו רואים שכל פתרון הוא צירוף לינארי של הוקטורים הללו עם הסקלרים שהם הפרמטרים (במקרה זה | + | |
*וקטורים אלה תמיד בת"ל, שכן אם יש צירוף לינארי שלהם שמתאפס, מכיוון שהפרמטרים תמיד מופיעים לבדם בעמודה של המשתנה שלהם, הם חייבים להיות אפס | *וקטורים אלה תמיד בת"ל, שכן אם יש צירוף לינארי שלהם שמתאפס, מכיוון שהפרמטרים תמיד מופיעים לבדם בעמודה של המשתנה שלהם, הם חייבים להיות אפס | ||
| − | + | לכן הבסיס למרחב האפס הנו <math>\bigl\{(-1,0,0,1),(-1,1,1,0)\bigr\}</math> | |
| − | לכן הבסיס למרחב האפס | + | |
===אלגוריתם למציאת '''שלושת''' מרחבי המטריצה=== | ===אלגוריתם למציאת '''שלושת''' מרחבי המטריצה=== | ||
#דרג את המטריצה (ניתן גם לדרג קנונית אך לא חובה) | #דרג את המטריצה (ניתן גם לדרג קנונית אך לא חובה) | ||
#'''השורות השונות מאפס''' מהוות בסיס למרחב השורה | #'''השורות השונות מאפס''' מהוות בסיס למרחב השורה | ||
| − | #'''העמודות במטריצה המקורית''' המהוות עמודות ציר (כלומר יש | + | #'''העמודות במטריצה המקורית''' המהוות עמודות ציר (כלומר יש אבר פותח בעמודה בצורה הקנונית), מהוות בסיס למרחב העמודה |
#הצב פרמטרים במקום המשתנים החופשיים | #הצב פרמטרים במקום המשתנים החופשיים | ||
#מצא את הפתרון הכללי | #מצא את הפתרון הכללי | ||
#פרק את הפתרון הכללי לצירוף לינארי של וקטורים קבועים כפול הפרמטרים | #פרק את הפתרון הכללי לצירוף לינארי של וקטורים קבועים כפול הפרמטרים | ||
#'''הוקטורים הקבועים''' מהווים בסיס למרחב האפס | #'''הוקטורים הקבועים''' מהווים בסיס למרחב האפס | ||
| − | |||
'''שימו לב:''' בהנתן מרחב כלשהו (פולינומים, מטריצות, פונקציות) ניתן לבצע את החישובים על מרחב הקואורדינטות. כפי שראינו בשיעור שעבר, מציאת בסיס למרחבים רבים שקולה למציאת בסיס למרחב האפס של מטריצה מסוימת. | '''שימו לב:''' בהנתן מרחב כלשהו (פולינומים, מטריצות, פונקציות) ניתן לבצע את החישובים על מרחב הקואורדינטות. כפי שראינו בשיעור שעבר, מציאת בסיס למרחבים רבים שקולה למציאת בסיס למרחב האפס של מטריצה מסוימת. | ||
| − | ===סיכום בנושא | + | ===סיכום בנושא ממדי מרחבים המטריצה והדרגה=== |
| − | תהי A מטריצה. המספרים הבאים שווים (זה נובע מהחומר שלמדנו עד עכשיו): | + | תהי <math>A</math> מטריצה. המספרים הבאים שווים (זה נובע מהחומר שלמדנו עד עכשיו): |
*דרגת המטריצה | *דרגת המטריצה | ||
| − | * | + | *ממד מרחב העמודות |
| − | * | + | *ממד מרחב השורות |
*מספר השורות השונות מאפס בצורה הקנונית | *מספר השורות השונות מאפס בצורה הקנונית | ||
| − | *מספר | + | *מספר האברים הפותחים |
*מספר עמודות הציר | *מספר עמודות הציר | ||
*מספר המשתנים התלויים | *מספר המשתנים התלויים | ||
| − | |||
המספרים הבאים שווים: | המספרים הבאים שווים: | ||
*מספר המשתנים החופשיים | *מספר המשתנים החופשיים | ||
| − | * | + | *ממד מרחב הפתרונות של המערכת ההומוגנית |
| − | מכיוון שמספר המשתנים החופשיים ועוד מספר המשתנים התלויים שווה לסך כל המשתנים, וזהו מספר העמודות במטריצה, נובע שדרגת המטריצה ועוד | + | מכיוון שמספר המשתנים החופשיים ועוד מספר המשתנים התלויים שווה לסך כל המשתנים, וזהו מספר העמודות במטריצה, נובע שדרגת המטריצה ועוד ממד מרחב הפתרונות שווים למספר העמודות מ. |
'''תרגיל.''' | '''תרגיל.''' | ||
| − | הוכח כי לכל מטריצה <math>A\in\ | + | הוכח כי לכל מטריצה <math>A\in\R^{m\times n}</math> מתקיים <math>\R^n=R(A)\oplus N(A)</math> |
'''פתרון.''' | '''פתרון.''' | ||
| − | מכיוון שהרגע ראינו כי סכום | + | מכיוון שהרגע ראינו כי סכום הממדים מקיים <math>\dim R(A)+\dim N(A)=n</math> לפי משפט הממדים מספיק להוכיח שהחיתוך בינהם הנו אפס. |
| − | נניח | + | נניח שקיים <math>v</math> השייך למרחב הפתרונות וגם למרחב השורות. מכיוון שהוא שייך למרחב השורות, ניתן להפעיל פעולות שורה על המטריצה כך שאחת משורותיה תהפוך להיות <math>v</math> , בלי הגבלת הכלליות תהא זו השורה הראשונה. |
| − | מכיוון | + | מכיוון ש־<math>v</math> במרחב הפתרונות של <math>A</math> , הוא גם במרחב הפתרונות של המטריצה לאחרת פעולות השורה <math>B</math> , ומתקיים <math>Bv=0</math> . אבל האבר הראשון במכפלה שווה <math>0=R_1(A)v=v^tv</math> וכפי שלמדנו זהו סכום ריבועים שמתאפס ולכן <math>v=0</math> כפי שרצינו. |
גרסה אחרונה מ־14:16, 2 בספטמבר 2018
תהי מטריצה 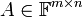 . מגדירים שלושה מרחבים עיקריים:
. מגדירים שלושה מרחבים עיקריים:
- מרחב השורות של
 . זהו המרחב הנפרש על ידי שורות המטריצה. נסמן
. זהו המרחב הנפרש על ידי שורות המטריצה. נסמן 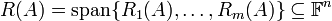
- מרחב העמודות של
 . זהו המרחב הנפרש על ידי עמודות המטריצה. נסמן
. זהו המרחב הנפרש על ידי עמודות המטריצה. נסמן 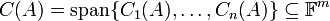
- מרחב האפס של
 . זהו מרחב הפתרונות של המערכת ההומוגנית
. זהו מרחב הפתרונות של המערכת ההומוגנית 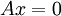 . נסמן
. נסמן 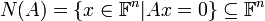
הגדרה: דרגת המטריצה  שווה למספר השורות בצורה המדורגת שלה השונות מאפס. מסומן
שווה למספר השורות בצורה המדורגת שלה השונות מאפס. מסומן 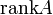 .
.
משפט: 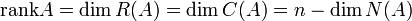 . אלה שווים למספר המשתנים התלויים, וממד מרחב האפס שווה למספר המשתנים החופשיים.
. אלה שווים למספר המשתנים התלויים, וממד מרחב האפס שווה למספר המשתנים החופשיים.
דוגמא. מצא בסיס למרחב האפס של המטריצה 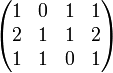
ראשית, נדרג קנונית את המטריצה לקבלת
לפיכך המשתנה השלישי והרביעי הם חופשיים, נציב במקומם פרמטרים 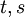 והפתרון הכללי הוא מהצורה
והפתרון הכללי הוא מהצורה 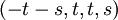 . תמיד ניתן לפרק את הפתרון הכללי לסכום של וקטורים קבועים כפול הסקלרים שהם הפרמטרים:
. תמיד ניתן לפרק את הפתרון הכללי לסכום של וקטורים קבועים כפול הסקלרים שהם הפרמטרים: 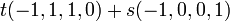 . וקטורים קבועים אלה תמיד מהווים בסיס למרחב הפתרונות:
. וקטורים קבועים אלה תמיד מהווים בסיס למרחב הפתרונות:
- אנו רואים שכל פתרון הוא צירוף לינארי של הוקטורים הללו עם הסקלרים שהם הפרמטרים (במקרה זה
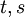 )
) - וקטורים אלה תמיד בת"ל, שכן אם יש צירוף לינארי שלהם שמתאפס, מכיוון שהפרמטרים תמיד מופיעים לבדם בעמודה של המשתנה שלהם, הם חייבים להיות אפס
לכן הבסיס למרחב האפס הנו 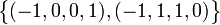
אלגוריתם למציאת שלושת מרחבי המטריצה
- דרג את המטריצה (ניתן גם לדרג קנונית אך לא חובה)
- השורות השונות מאפס מהוות בסיס למרחב השורה
- העמודות במטריצה המקורית המהוות עמודות ציר (כלומר יש אבר פותח בעמודה בצורה הקנונית), מהוות בסיס למרחב העמודה
- הצב פרמטרים במקום המשתנים החופשיים
- מצא את הפתרון הכללי
- פרק את הפתרון הכללי לצירוף לינארי של וקטורים קבועים כפול הפרמטרים
- הוקטורים הקבועים מהווים בסיס למרחב האפס
שימו לב: בהנתן מרחב כלשהו (פולינומים, מטריצות, פונקציות) ניתן לבצע את החישובים על מרחב הקואורדינטות. כפי שראינו בשיעור שעבר, מציאת בסיס למרחבים רבים שקולה למציאת בסיס למרחב האפס של מטריצה מסוימת.
סיכום בנושא ממדי מרחבים המטריצה והדרגה
תהי  מטריצה. המספרים הבאים שווים (זה נובע מהחומר שלמדנו עד עכשיו):
מטריצה. המספרים הבאים שווים (זה נובע מהחומר שלמדנו עד עכשיו):
- דרגת המטריצה
- ממד מרחב העמודות
- ממד מרחב השורות
- מספר השורות השונות מאפס בצורה הקנונית
- מספר האברים הפותחים
- מספר עמודות הציר
- מספר המשתנים התלויים
המספרים הבאים שווים:
- מספר המשתנים החופשיים
- ממד מרחב הפתרונות של המערכת ההומוגנית
מכיוון שמספר המשתנים החופשיים ועוד מספר המשתנים התלויים שווה לסך כל המשתנים, וזהו מספר העמודות במטריצה, נובע שדרגת המטריצה ועוד ממד מרחב הפתרונות שווים למספר העמודות מ.
תרגיל.
הוכח כי לכל מטריצה 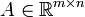 מתקיים
מתקיים 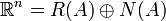
פתרון.
מכיוון שהרגע ראינו כי סכום הממדים מקיים 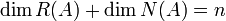 לפי משפט הממדים מספיק להוכיח שהחיתוך בינהם הנו אפס.
לפי משפט הממדים מספיק להוכיח שהחיתוך בינהם הנו אפס.
נניח שקיים 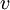 השייך למרחב הפתרונות וגם למרחב השורות. מכיוון שהוא שייך למרחב השורות, ניתן להפעיל פעולות שורה על המטריצה כך שאחת משורותיה תהפוך להיות
השייך למרחב הפתרונות וגם למרחב השורות. מכיוון שהוא שייך למרחב השורות, ניתן להפעיל פעולות שורה על המטריצה כך שאחת משורותיה תהפוך להיות 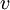 , בלי הגבלת הכלליות תהא זו השורה הראשונה.
, בלי הגבלת הכלליות תהא זו השורה הראשונה.
מכיוון ש־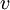 במרחב הפתרונות של
במרחב הפתרונות של  , הוא גם במרחב הפתרונות של המטריצה לאחרת פעולות השורה
, הוא גם במרחב הפתרונות של המטריצה לאחרת פעולות השורה  , ומתקיים
, ומתקיים 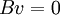 . אבל האבר הראשון במכפלה שווה
. אבל האבר הראשון במכפלה שווה 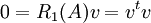 וכפי שלמדנו זהו סכום ריבועים שמתאפס ולכן
וכפי שלמדנו זהו סכום ריבועים שמתאפס ולכן 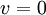 כפי שרצינו.
כפי שרצינו.