משפט בולצאנו-ויירשטראס

משפט בולצאנו ויירשטראס לסדרות

לכל סדרה חסומה יש תת סדרה מתכנסת

הוכחה

ראשית, נזכר בלמה של קנטור. יהי 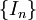$\{I_n\}$ אוסף של קטעים סגורים $I_n=[a_n,b_n]$ כך שכל אחד מוכל בקודמו (כלומר $a_n$ מונוטונית לא יורדת, ו$b_n$ מונוטונית לא עולה). עוד נניח כי אורך הקטעים שואף לאפס, כלומר $\lim_{n\rightarrow\infty}b_n-a_n =0$.

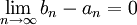אזי קיימת נקודה יחידה השייכת לכל הקטעים. (מתקיים באופן טבעי שנקודה זו שווה לגבול הסדרות 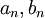$a_n,b_n$.)

נביט כעת בסדרה חסומה 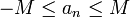$-M\leq a_n \leq M$ (זכרו, הסדרה לא חייבת להיות בכל הקטע הזה, רק לא לצאת ממנו). כיוון שבסדרה ישנם אינסוף איברים, הקטע $I_1:=[-M,M]$ מכיל אינסוף איברים מהסדרה.

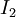נביט כעת בשני חצאי הקטע $[-M,0],[0,M]$. בהכרח אחד מהם לפחות מכיל אינסוף איברים מהסדרה (וזה עיקר הרעיון של ההוכחה). נסמן את חצי הקטע הזה ב $I_2$. נחצה את הקטע הזה לשניים, ונבחר חצי שמכיל אינסוף איברים.

אם כך, קיבלנו סדרה של קטעים 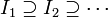$I_1\supseteq I_2 \supseteq \cdots$ המקיימת את התכונות הבאות:

• כל קטע מכיל אינסוף איברים מהסדרה $a_n$

• כל קטע מוכל בקודמו

• אורך כל קטע הוא חצי קודמו. כיוון שאורך הקטע הראשון הינו 2M אורך הקטע 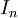$I_n$ שווה ל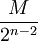$\frac{M}{2^{n-2}}$. ברור שאורך הקטעים שואף לאפס לכן.

לפי הלמה של קנטור, מתקיים כי יש נקודה המוכל בכל הקטעים הללו, נקרא לה L. נוכיח כי L הינו גבול חלקי של $a_n$ ובכך נסיים את ההוכחה (שכן ההגדרה של גבול חלקי הינו קיום תת סדרה השואפת אליו).

• יהי אפסילון גדול מאפס, רוצים להוכיח כי בסביבת אפסילון של L ישנם אינסוף איברים מהסדרה.
• כיוון שאורך הקטעים שבנינו שואפים לאפס, יש קטע שאורכו קטן מאפסילון חלקי 2.
• לפי ההגדרה של L מהלמה של קנטור, L מוכל בכל הקטעים שבנינו ובפרט בקטע הקטן הזה.
• לכן בוודאי הקטע הקטן מוכל בסביבת אפסילון של L.
• אבל אחת התכונות של הקטעים שבנינו היא שהם מכילים אינסוף איברים מהסדרה ולכן קיימים אינסוף איברים מהסדרה בסביבת אפסילון של L.

כפי שרצינו להוכיח.