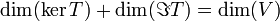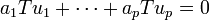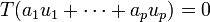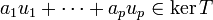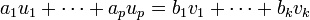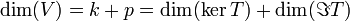הבדלים בין גרסאות בדף "משפט הדרגה"
מתוך Math-Wiki
(יצירת דף עם התוכן "=משפט הדרגה= יהיו V,W מ"ו נוצרים סופית, ותהי העתקה לינארית <math>T:V\rightarrow W</math>. אזי מתקיים: ::<math>di...") |
יהודה שמחה (שיחה | תרומות) |
||
| (5 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | חזרה ל[[משפטים/לינארית|משפטים בלינארית]] | ||
| + | |||
=משפט הדרגה= | =משפט הדרגה= | ||
| − | יהיו V,W מ"ו נוצרים סופית, ותהי העתקה לינארית <math>T:V\ | + | יהיו <math>V,W</math> מ"ו נוצרים סופית, ותהי העתקה לינארית <math>T:V\to W</math> . אזי מתקיים: |
| − | + | :<math>\dim(\ker T)+\dim(\Im T)=\dim(V)</math> | |
| − | + | ||
=הוכחה= | =הוכחה= | ||
| + | נסמן את הבסיס לגרעין ב־<math>\{v_1,\ldots,v_k\}</math> . | ||
| + | |||
| + | נשלים את הבסיס הזה לבסיס ל־<math>V</math> , נסמנו <math>\{v_1,\ldots,v_k,u_1,\ldots,u_p\}</math> . | ||
| + | |||
| + | נוכיח כי <math>E=\{Tu_1,\ldots,Tu_p\}</math> בסיס לתמונה, ומכאן נסיק בקלות את המשפט. | ||
| + | |||
| + | ===E פורש את ImT=== | ||
| + | כיוון שכל וקטור ב־<math>V</math> הנו צירוף לינארי של אברי הבסיס, <math>T</math> שולחת כל וקטור לצירוף לינארי של תמונות אברי הבסיס. | ||
| + | |||
| + | לכן, באופן כללי, בהנתן בסיס ל־<math>V</math> התמונות של אברי הבסיס '''פורשות''' (אך לא בהכרח בסיס) לתמונה של <math>T</math> . | ||
| + | |||
| + | כלומר <math>\Im T=\text{span}\{Tv_1,\ldots,Tv_k,Tu_1,\ldots,Tu_p\}</math> . | ||
| + | |||
| + | |||
| + | ברור כי <math>Tv_1=\cdots=Tv_k=0</math> (הרי בחרנו את <math>v_1,\ldots,v_k</math> להיות בסיס לגרעין). | ||
| + | |||
| + | לכן מתקיים <math>\Im T=\text{span}\{Tu_1,\ldots,Tu_p\}</math> . | ||
| + | |||
| + | ===E בת"ל=== | ||
| + | ניקח צירוף לינארי מתאפס של אברי <math>E</math> : | ||
| + | :<math>a_1Tu_1+\cdots+a_pTu_p=0</math> | ||
| + | לכן | ||
| + | :<math>T(a_1u_1+\cdots+a_pu_p)=0</math> | ||
| + | לכן | ||
| + | :<math>a_1u_1+\cdots+a_pu_p\in\ker T</math> | ||
| + | ולכן קיים צירוף לינארי של אברי הבסיס לגרעין עבורו | ||
| + | :<math>a_1u_1+\cdots+a_pu_p=b_1v_1+\cdots+b_kv_k</math> | ||
| + | נעביר אגף לקבל צירוף לינארי מתאפס של אברי הבסיס של <math>V</math> , ולכן כל המקדמים הם 0. | ||
| + | |||
| + | לכן <math>E</math> בת"ל. | ||
| + | |||
| + | ===ספירת ממדים וסיכום=== | ||
| + | הוכחנו אפוא, כי <math>E</math> הנו בסיס לתמונה, ולכן יש לנו בסיסים וממדים לכל תת־המרחבים המעורבים בעניין. | ||
| + | :<math>\dim(V)=k+p=\dim(\ker T)+\dim(\Im T)</math> | ||
| + | |||
| + | [[קטגוריה:אלגברה לינארית]] | ||
גרסה אחרונה מ־14:09, 2 בספטמבר 2018
חזרה למשפטים בלינארית
תוכן עניינים
משפט הדרגה
יהיו 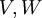 מ"ו נוצרים סופית, ותהי העתקה לינארית
מ"ו נוצרים סופית, ותהי העתקה לינארית 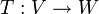 . אזי מתקיים:
. אזי מתקיים:
הוכחה
נסמן את הבסיס לגרעין ב־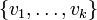 .
.
נשלים את הבסיס הזה לבסיס ל־ , נסמנו
, נסמנו 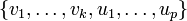 .
.
נוכיח כי 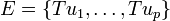 בסיס לתמונה, ומכאן נסיק בקלות את המשפט.
בסיס לתמונה, ומכאן נסיק בקלות את המשפט.
E פורש את ImT
כיוון שכל וקטור ב־ הנו צירוף לינארי של אברי הבסיס,
הנו צירוף לינארי של אברי הבסיס,  שולחת כל וקטור לצירוף לינארי של תמונות אברי הבסיס.
שולחת כל וקטור לצירוף לינארי של תמונות אברי הבסיס.
לכן, באופן כללי, בהנתן בסיס ל־ התמונות של אברי הבסיס פורשות (אך לא בהכרח בסיס) לתמונה של
התמונות של אברי הבסיס פורשות (אך לא בהכרח בסיס) לתמונה של  .
.
כלומר 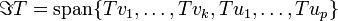 .
.
ברור כי 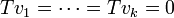 (הרי בחרנו את
(הרי בחרנו את 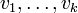 להיות בסיס לגרעין).
להיות בסיס לגרעין).
לכן מתקיים 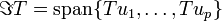 .
.
E בת"ל
ניקח צירוף לינארי מתאפס של אברי  :
:
לכן
לכן
ולכן קיים צירוף לינארי של אברי הבסיס לגרעין עבורו
נעביר אגף לקבל צירוף לינארי מתאפס של אברי הבסיס של  , ולכן כל המקדמים הם 0.
, ולכן כל המקדמים הם 0.
לכן  בת"ל.
בת"ל.
ספירת ממדים וסיכום
הוכחנו אפוא, כי  הנו בסיס לתמונה, ולכן יש לנו בסיסים וממדים לכל תת־המרחבים המעורבים בעניין.
הנו בסיס לתמונה, ולכן יש לנו בסיסים וממדים לכל תת־המרחבים המעורבים בעניין.