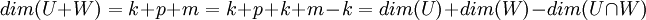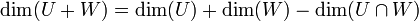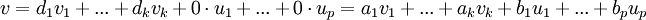הבדלים בין גרסאות בדף "משפט המימדים"
יהודה שמחה (שיחה | תרומות) מ |
|||
| שורה 2: | שורה 2: | ||
=משפט המימדים= | =משפט המימדים= | ||
| − | יהי V מ"ו נוצר סופית ויהיו U,W תתי מרחב של V. אזי: | + | יהי <math>V</math> מ"ו נוצר סופית ויהיו <math>U,W</math> תתי-מרחב של <math>V</math> . אזי: |
| − | :<math>dim(U+W)=dim(U)+dim(W)-dim(U\cap W)</math> | + | :<math>\dim(U+W)=\dim(U)+\dim(W)-\dim(U\cap W)</math> |
=הוכחה= | =הוכחה= | ||
| + | נסמן את הבסיס ל- <math>U\cap W</math> ב- <math>\{v_1,v_2,\dots,v_k\}</math> . | ||
| − | + | כיון ש- <math>U\cap W\subseteq U,W</math> , ניתן להשלים את בסיס החיתוך לבסיס ל- <math>U</math> ובאופן דומה לבסיס ל- <math>W</math> . | |
| − | + | נסמן את הבסיסים ב- <math>\{v_1,\dots,v_k,u_1,\dots,u_p\},\{v_1,\dots,v_k,w_1,\dots,w_m\}</math> . | |
| − | נסמן את הבסיסים ב <math>\{v_1, | + | נסמן את איחוד הבסיסים ב- <math>B=\{v_1,\dots,v_k,u_1,\dots,u_p,w_1,\dots,w_m\}</math> , ונוכיח כי <math>B</math> הנו בסיס ל- <math>U+W</math> . |
| − | + | ===<math>B</math> פורש את <math>U+W</math>=== | |
| − | + | יהי <math>u+w\in U+W</math> . אזי נציג את הוקטורים כצירוף לינארי של הבסיסים, <math>u+w=a_1v_1+\cdots+a_kv_k+b_1u_1+\cdots+b_pu_p+c_1v_1+\cdots+c_kv_k+d_1w_1+\cdots+d_mw_m</math>. | |
| − | + | ||
| − | + | ||
| − | יהי <math>u+w\in U+W</math>. אזי נציג את הוקטורים כצירוף לינארי של הבסיסים, <math>u+w=a_1v_1+ | + | |
ברור אם כך כי <math>u+w\in span(B)</math> | ברור אם כך כי <math>u+w\in span(B)</math> | ||
| − | ===B בת"ל=== | + | ===<math>B</math> בת"ל=== |
| − | + | ||
ניקח צירוף לינארי מתאפס כלשהו של איברי B: | ניקח צירוף לינארי מתאפס כלשהו של איברי B: | ||
גרסה מ־18:02, 27 בפברואר 2016
חזרה למשפטים בלינארית
תוכן עניינים
משפט המימדים
יהי  מ"ו נוצר סופית ויהיו
מ"ו נוצר סופית ויהיו 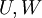 תתי-מרחב של
תתי-מרחב של  . אזי:
. אזי:
הוכחה
נסמן את הבסיס ל- 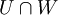 ב-
ב- 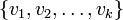 .
.
כיון ש- 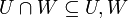 , ניתן להשלים את בסיס החיתוך לבסיס ל-
, ניתן להשלים את בסיס החיתוך לבסיס ל- 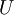 ובאופן דומה לבסיס ל-
ובאופן דומה לבסיס ל- 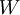 .
.
נסמן את הבסיסים ב- 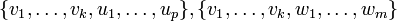 .
.
נסמן את איחוד הבסיסים ב- 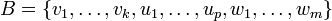 , ונוכיח כי
, ונוכיח כי  הנו בסיס ל-
הנו בסיס ל- 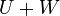 .
.
 פורש את
פורש את 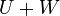
יהי 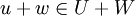 . אזי נציג את הוקטורים כצירוף לינארי של הבסיסים,
. אזי נציג את הוקטורים כצירוף לינארי של הבסיסים, 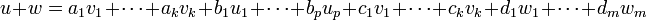 .
.
ברור אם כך כי 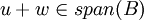
 בת"ל
בת"ל
ניקח צירוף לינארי מתאפס כלשהו של איברי B:
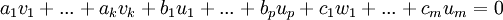 .
.
נסמן 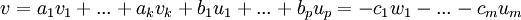
ברור משני אגפי המשוואה כי 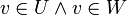 ולכן
ולכן 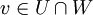
לכן ל-v יש הצגה כצירוף לינארי של איברי הבסיס לחיתוך, 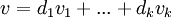 .
.
כמו כן, ל-v יש הצגה יחידה כצירוף לינארי של איברי הבסיס של U ולכן מתקיים:
ולכן 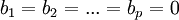 .
.
כעת קיבלנו כי 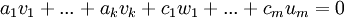 ,
,
אבל זה צירוף לינארי של איברי הבסיס של W ולכן הוא טריוויאלי.
מכאן שהצירוף הלינארי היחיד שמתאפס של איברי B הינו הטריוויאלי ולכן B בת"ל.
ספירת מימדים וסיכום
מצאנו, איפוא, בסיסים לכל תתי המרחבים המוזכרים במשפט, נותר רק לוודא שאכן הנוסחא עובדת: