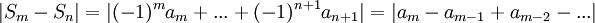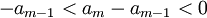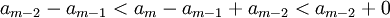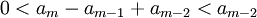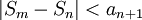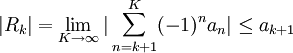הבדלים בין גרסאות בדף "משפט לייבניץ"
מתוך Math-Wiki
(יצירת דף עם התוכן "חזרה למשפטים באינפי ==משפט לייבניץ לטורים עם סימנים מתחלפים== תהי <math>a_n</math>...") |
(←הוכחה) |
||
| שורה 9: | שורה 9: | ||
===הוכחה=== | ===הוכחה=== | ||
| + | נוכיח כי סדרה הסכומים החלקיים של הטור הינה סדרת קושי, ועל כן הטור מתכנס. | ||
| + | |||
| + | יהי אפסילון גדול מאפס, צריך למצוא מקום בסדרה שהחל ממנו והלאה ההפרש בין כל שני איברים קטן מאפסילון. | ||
| + | |||
| + | *<math>|S_m-S_n|=|(-1)^ma_m+...+(-1)^{n+1}a_{n+1}|=|a_m-a_{m-1}+a_{m-2}-...| </math> | ||
| + | |||
| + | נראה כי כל איבר "בולע" את קודמיו, לפי המונוטוניות של הסדרה: | ||
| + | |||
| + | ::<math>-a_{m-1}<a_m-a_{m-1}<0</math> | ||
| + | |||
| + | לכן | ||
| + | |||
| + | ::<math>a_{m-2}-a_{m-1}<a_m-a_{m-1}+a_{m-2}<a_{m-2}+0</math> | ||
| + | |||
| + | כלומר | ||
| + | |||
| + | ::<math>0<a_m-a_{m-1}+a_{m-2}<a_{m-2}</math> | ||
| + | |||
| + | וכן הלאה עד שנקבל | ||
| + | |||
| + | ::<math>|S_m-S_n|<a_{n+1}</math> | ||
| + | |||
| + | |||
| + | וכיוון ש<math>a_n</math> שואפת לאפס, החל ממקום מסויים זה קטן מאפסילון (ללא תלות ב-m). | ||
| + | |||
| + | |||
| + | לפי טיעון דומה, <math>|\sum_{n=k+1}^K (-1)^na_n|=|a_{k+1}-a_{k+2}+a_{k+3}-...|\leq a_{k+1}</math> ולכן | ||
| + | |||
| + | ::<math>|R_k|=\lim_{K\rightarrow \infty}|\sum_{n=k+1}^K (-1)^na_n|\leq a_{k+1}</math> | ||
| + | |||
| + | כפי שרצינו. | ||
גרסה מ־10:37, 2 בפברואר 2012
משפט לייבניץ לטורים עם סימנים מתחלפים
תהי  סדרה חיובית, מונוטונית, השואפת לאפס. אזי:
סדרה חיובית, מונוטונית, השואפת לאפס. אזי:
- הטור
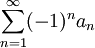 מתכנס
מתכנס - השארית
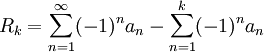 מקיימת
מקיימת 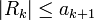
הוכחה
נוכיח כי סדרה הסכומים החלקיים של הטור הינה סדרת קושי, ועל כן הטור מתכנס.
יהי אפסילון גדול מאפס, צריך למצוא מקום בסדרה שהחל ממנו והלאה ההפרש בין כל שני איברים קטן מאפסילון.
נראה כי כל איבר "בולע" את קודמיו, לפי המונוטוניות של הסדרה:
לכן
כלומר
וכן הלאה עד שנקבל
וכיוון ש שואפת לאפס, החל ממקום מסויים זה קטן מאפסילון (ללא תלות ב-m).
שואפת לאפס, החל ממקום מסויים זה קטן מאפסילון (ללא תלות ב-m).
לפי טיעון דומה, 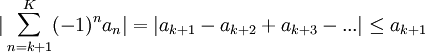 ולכן
ולכן
כפי שרצינו.