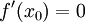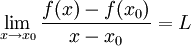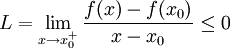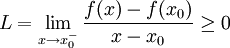|
|
| שורה 40: |
שורה 40: |
| | סה"כ <math>L=0</math> כפי שרצינו. | | סה"כ <math>L=0</math> כפי שרצינו. |
| | | | |
| | + | == ראו גם == |
| | | | |
| − | ==משפט רול==
| + | * [[משפט רול]] |
| − | | + | * [[משפט לגרנאז' (אינפי)|משפט לגרנאז']] |
| − | תהי f רציפה בקטע <math>[a,b]</math> וגזירה בקטע <math>(a,b)</math> כך ש <math>f(a)=f(b)</math>.
| + | |
| − | | + | |
| − | אזי קיימת נקודה <math>c\in (a,b)</math> עבורה מתקיים <math>f'(c)=0</math>
| + | |
| − | | + | |
| − | | + | |
| − | ===הוכחה===
| + | |
| − | נוכיח כי קיימת נקודת קיצון מקומית <math>c\in (a,b)</math> ולכן המשל נובע ממשפט פרמה.
| + | |
| − | | + | |
| − | לפי משפט ויישטראס השני, כיוון שהפונקציה רציפה בקטע סגור היא מקבלת בו מינימום ומקסימום. נניח בשלילה שגם המינימום וגם המקסימום מתקבלים בקצות הקטע a,b. על כן, כיוון ש<math>f(a)=f(b)</math> אנו מקבלים כי המקסימום והמינימום שווים ולכן הפונקציה קבועה בקטע. לכן כל נקודה בקטע היא נקודת קיצון מקומית, וקיבלנו את התוצאה הדרושה.
| + | |
| − | | + | |
| − | אחרת, המינימום או המקסימום מתקבלים בקטע הפתוח <math>(a,b)</math> ולכן הן נקודות קיצון מקומיות, ושוב קיבלנו את התוצאה הדרושה.
| + | |
| − | | + | |
| − | | + | |
| − | ==משפט לגראנז'==
| + | |
| − | תהי f רציפה בקטע <math>[a,b]</math> וגזירה בקטע <math>(a,b)</math>.
| + | |
| − | | + | |
| − | אזי קיימת נקודה <math>c\in (a,b)</math> עבורה מתקיים <math>f'(c)=\frac{f(b)-f(a)}{b-a}</math>
| + | |
| − | | + | |
| − | | + | |
| − | ===הוכחה===
| + | |
| − | | + | |
| − | נחשב את משוואת הישר העובר בין הנקודות <math>(a,f(a)),(b,f(b))</math>:
| + | |
| − | | + | |
| − | ::<math>y-f(a)=\frac{f(b)-f(a)}{b-a}(x-a)</math>
| + | |
| − | | + | |
| − | נחסיר את משוואת הישר הזה מהפונקציה המקורית, ונוכל להפעיל את משפט רול על מנת לקבל את התוצאה הרצוייה.
| + | |
| − | | + | |
| − | | + | |
| − | ::<math>g(x)=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a)</math>
| + | |
| − | | + | |
| − | | + | |
| − | קל לראות כי <math>g(a)=g(b)=0</math> ו-g מקיימת את שאר תנאיי משפט רול. לכן קיימת נקודה <math>c\in (a,b)</math> עבורה מתקיים <math>g'(c)=0</math>. אבל:
| + | |
| − | | + | |
| − | | + | |
| − | ::<math>0=g'(c)=f'(c)-\frac{f(b)-f(a)}{b-a}</math>
| + | |
| − | | + | |
| − | כלומר
| + | |
| − | | + | |
| − | ::<math>f'(c)=\frac{f(b)-f(a)}{b-a}</math>
| + | |
| − | | + | |
| − | כפי שרצינו.
| + | |
| | | | |
| | [[קטגוריה:אינפי]] | | [[קטגוריה:אינפי]] |
גרסה מ־01:01, 15 בפברואר 2012
הגדרת נקודת קיצון מקומית
תהי  מוגדרת בסביבת הנקודה
מוגדרת בסביבת הנקודה  כך שלכל x בסביבה מתקיים:
כך שלכל x בסביבה מתקיים:
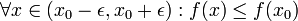 (נקודת מקסימום מקומי)
(נקודת מקסימום מקומי)
או
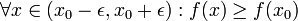 (נקודת מינימום מקומי)
(נקודת מינימום מקומי)
אזי  הינה נקודת קיצון מקומית של
הינה נקודת קיצון מקומית של  .
.
משפט פרמה
תהי  נקודת קיצון מקומית של פונקציה
נקודת קיצון מקומית של פונקציה  . אזי אם
. אזי אם  גזירה ב
גזירה ב מתקיים:
מתקיים:
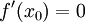
הוכחה
נניח כי f גזירה בנקודת מקסימום מקומי  (ההוכחה עבור מינימום דומה) . אזי לפי הגדרת הנגזרת הגבול הבא קיים:
(ההוכחה עבור מינימום דומה) . אזי לפי הגדרת הנגזרת הגבול הבא קיים:
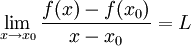
לפי משפט, כיוון שהגבול קיים, הגבולות החד צדדיים ושווים.
לפי הנתון, קיימת סביבה ימנית של  בה מתקיים
בה מתקיים 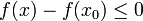 , וכיוון שזו סביבה ימנית מתקיים בה גם
, וכיוון שזו סביבה ימנית מתקיים בה גם 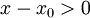 .
.
לכן ביחד, מתקיים כי
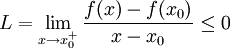
באופן דומה, קיימת סביבה שמאלית של  בה מתקיים
בה מתקיים 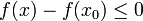 , וכיוון שזו סביבה שמאלית מתקיים בה גם
, וכיוון שזו סביבה שמאלית מתקיים בה גם 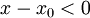 .
.
לכן ביחד, מתקיים כי
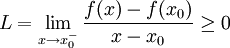
סה"כ 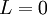 כפי שרצינו.
כפי שרצינו.
ראו גם
 מוגדרת בסביבת הנקודה
מוגדרת בסביבת הנקודה  כך שלכל x בסביבה מתקיים:
כך שלכל x בסביבה מתקיים:
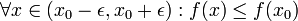 (נקודת מקסימום מקומי)
(נקודת מקסימום מקומי)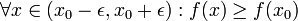 (נקודת מינימום מקומי)
(נקודת מינימום מקומי) הינה נקודת קיצון מקומית של
הינה נקודת קיצון מקומית של  .
.
 נקודת קיצון מקומית של פונקציה
נקודת קיצון מקומית של פונקציה  . אזי אם
. אזי אם  גזירה ב
גזירה ב מתקיים:
מתקיים:
 (ההוכחה עבור מינימום דומה) . אזי לפי הגדרת הנגזרת הגבול הבא קיים:
(ההוכחה עבור מינימום דומה) . אזי לפי הגדרת הנגזרת הגבול הבא קיים:
 בה מתקיים
בה מתקיים 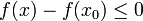 , וכיוון שזו סביבה ימנית מתקיים בה גם
, וכיוון שזו סביבה ימנית מתקיים בה גם 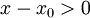 .
.
 בה מתקיים
בה מתקיים 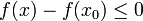 , וכיוון שזו סביבה שמאלית מתקיים בה גם
, וכיוון שזו סביבה שמאלית מתקיים בה גם 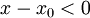 .
.
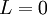 כפי שרצינו.
כפי שרצינו.