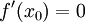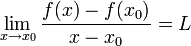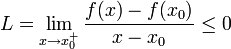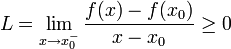הבדלים בין גרסאות בדף "משפט פרמה (אינפי)"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) |
|||
| (3 גרסאות ביניים של 3 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
==הגדרת נקודת קיצון מקומית== | ==הגדרת נקודת קיצון מקומית== | ||
| − | תהי <math>f</math> מוגדרת בסביבת הנקודה <math>x_0</math> כך שלכל | + | תהי <math>f</math> מוגדרת בסביבת הנקודה <math>x_0</math> כך שלכל <math>x</math> בסביבה מתקיים: |
| − | + | ||
| − | + | ||
| + | :<math>\forall x\in(x_0-\epsilon,x_0+\epsilon):f(x)\le f(x_0)</math> (נקודת מקסימום מקומי) | ||
'''או''' | '''או''' | ||
| + | :<math>\forall x\in(x_0-\epsilon,x_0+\epsilon):f(x)\ge f(x_0)</math> (נקודת מינימום מקומי) | ||
| − | + | אזי <math>x_0</math> הנה '''נקודת קיצון מקומית''' של <math>f</math> . | |
| − | + | ||
| − | + | ||
| − | אזי <math>x_0</math> | + | |
==משפט פרמה== | ==משפט פרמה== | ||
| − | + | תהי <math>x_0</math> נקודת קיצון מקומית של פונקציה <math>f</math> . אזי אם <math>f</math> גזירה ב- <math>x_0</math> מתקיים: | |
| − | תהי <math>x_0</math> נקודת קיצון מקומית של פונקציה <math>f</math>. אזי אם <math>f</math> גזירה ב<math>x_0</math> מתקיים: | + | :<math>f'(x_0)=0</math> |
| − | + | ||
| − | + | ||
===הוכחה=== | ===הוכחה=== | ||
| + | נניח כי <math>f</math> גזירה בנקודת '''מקסימום''' מקומי <math>x_0</math> (ההוכחה עבור מינימום דומה). אזי לפי הגדרת הנגזרת הגבול הבא קיים: | ||
| + | :<math>\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=L</math> | ||
| − | + | לפי משפט, כיון שהגבול קיים, הגבולות החד-צדדיים ושווים. | |
| − | + | לפי הנתון, קיימת סביבה ימנית של <math>x_0</math> בה מתקיים <math>f(x)-f(x_0)\le 0</math> , וכיון שזו סביבה ימנית מתקיים בה גם <math>x-x_0>0</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | לפי הנתון, קיימת סביבה ימנית של <math>x_0</math> בה מתקיים <math>f(x)-f(x_0)\ | + | |
לכן ביחד, מתקיים כי | לכן ביחד, מתקיים כי | ||
| + | :<math>L=\lim_{x\to x_0^+}\frac{f(x)-f(x_0)}{x-x_0}\le 0</math> | ||
| + | באופן דומה, קיימת סביבה שמאלית של <math>x_0</math> בה מתקיים <math>f(x)-f(x_0)\le 0</math> , וכיון שזו סביבה שמאלית מתקיים בה גם <math>x-x_0<0</math> . | ||
| − | + | לכן ביחד, מתקיים כי | |
| − | + | :<math>L=\lim_{x\to x_0^-}\frac{f(x)-f(x_0)}{x-x_0}\ge 0</math> | |
| − | + | ||
| − | + | ||
| − | לכן ביחד, מתקיים כי | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | סה"כ <math>L=0</math> כפי שרצינו. <math>\blacksquare</math> | |
| − | + | ==ראו גם== | |
| + | *[[משפט רול]] | ||
| + | *[[משפט לגראנז' (אינפי)|משפט לגראנז']] | ||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
גרסה אחרונה מ־11:39, 7 ביוני 2016
תוכן עניינים
הגדרת נקודת קיצון מקומית
תהי  מוגדרת בסביבת הנקודה
מוגדרת בסביבת הנקודה  כך שלכל
כך שלכל  בסביבה מתקיים:
בסביבה מתקיים:
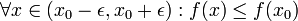 (נקודת מקסימום מקומי)
(נקודת מקסימום מקומי)
או
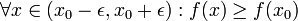 (נקודת מינימום מקומי)
(נקודת מינימום מקומי)
אזי  הנה נקודת קיצון מקומית של
הנה נקודת קיצון מקומית של  .
.
משפט פרמה
תהי  נקודת קיצון מקומית של פונקציה
נקודת קיצון מקומית של פונקציה  . אזי אם
. אזי אם  גזירה ב-
גזירה ב-  מתקיים:
מתקיים:
הוכחה
נניח כי  גזירה בנקודת מקסימום מקומי
גזירה בנקודת מקסימום מקומי  (ההוכחה עבור מינימום דומה). אזי לפי הגדרת הנגזרת הגבול הבא קיים:
(ההוכחה עבור מינימום דומה). אזי לפי הגדרת הנגזרת הגבול הבא קיים:
לפי משפט, כיון שהגבול קיים, הגבולות החד-צדדיים ושווים.
לפי הנתון, קיימת סביבה ימנית של  בה מתקיים
בה מתקיים 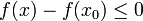 , וכיון שזו סביבה ימנית מתקיים בה גם
, וכיון שזו סביבה ימנית מתקיים בה גם 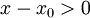 .
.
לכן ביחד, מתקיים כי
באופן דומה, קיימת סביבה שמאלית של  בה מתקיים
בה מתקיים 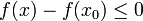 , וכיון שזו סביבה שמאלית מתקיים בה גם
, וכיון שזו סביבה שמאלית מתקיים בה גם 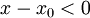 .
.
לכן ביחד, מתקיים כי
סה"כ 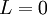 כפי שרצינו.
כפי שרצינו.