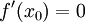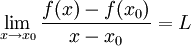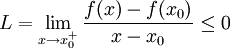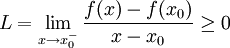משפט פרמה (אינפי)
מתוך Math-Wiki
גרסה מ־08:57, 2 בפברואר 2012 מאת ארז שיינר (שיחה | תרומות) (יצירת דף עם התוכן "חזרה למשפטים באינפי ==הגדרת נקודת קיצון מקומית== תהי <math>f</math> מוגדרת בסביבת ...")
הגדרת נקודת קיצון מקומית
תהי  מוגדרת בסביבת הנקודה
מוגדרת בסביבת הנקודה  כך שלכל x בסביבה מתקיים:
כך שלכל x בסביבה מתקיים:
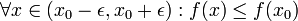 (נקודת מקסימום מקומי)
(נקודת מקסימום מקומי)
או
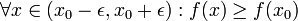 (נקודת מינימום מקומי)
(נקודת מינימום מקומי)
אזי  הינה נקודת קיצון מקומית של
הינה נקודת קיצון מקומית של  .
.
משפט פרמה
תהי  נקודת קיצון מקומית של פונקציה
נקודת קיצון מקומית של פונקציה  . אזי אם
. אזי אם  גזירה ב
גזירה ב מתקיים:
מתקיים:
הוכחה
נניח כי f גזירה בנקודת מקסימום מקומי  (ההוכחה עבור מינימום דומה) . אזי לפי הגדרת הנגזרת הגבול הבא קיים:
(ההוכחה עבור מינימום דומה) . אזי לפי הגדרת הנגזרת הגבול הבא קיים:
לפי משפט, כיוון שהגבול קיים, הגבולות החד צדדיים ושווים.
לפי הנתון, קיימת סביבה ימנית של  בה מתקיים
בה מתקיים 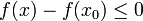 , וכיוון שזו סביבה ימנית מתקיים בה גם
, וכיוון שזו סביבה ימנית מתקיים בה גם 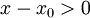 .
.
לכן ביחד, מתקיים כי
באופן דומה, קיימת סביבה שמאלית של  בה מתקיים
בה מתקיים 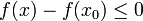 , וכיוון שזו סביבה שמאלית מתקיים בה גם
, וכיוון שזו סביבה שמאלית מתקיים בה גם 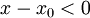 .
.
לכן ביחד, מתקיים כי
סה"כ 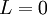 כפי שרצינו.
כפי שרצינו.