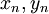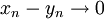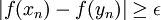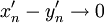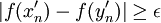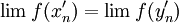הבדלים בין גרסאות בדף "משפט קנטור על רציפות במידה שווה"
מתוך Math-Wiki
(יצירת דף עם התוכן "חזרה למשפטים באינפי ==משפט קנטור לגבי פונקציות רציפות במ"ש== פונקציה רציפה ...") |
(←הוכחה) |
||
| שורה 5: | שורה 5: | ||
==הוכחה== | ==הוכחה== | ||
| + | תהי f רציפה על קטע סגור וסופי <math>[a,b]</math>. נניח בשלילה שהיא '''לא''' רציפה שם במ"ש. לכן קיים אפסילון גדול מאפס, כך שלכל דלתא גדול מאפס, יש שתי נקודות במרחק קטן מדלתא כך שהפרש התמונות שלהן גדול או שווה לאפסילון. ניתן אם כך לבנות סדרה של זוגות של נקודות | ||
| + | |||
| + | ::<math>x_n,y_n</math> | ||
| + | |||
| + | כך שמתקיים | ||
| + | |||
| + | ::<math>x_n-y_n\rightarrow 0</math> | ||
| + | |||
| + | אבל | ||
| + | |||
| + | ::<math>|f(x_n)-f(y_n)|\geq \epsilon</math> | ||
| + | |||
| + | |||
| + | לפי משפט [[משפטים/אינפי/בולצאנו-ויירשטראס|בולצאנו-ויירשטראס לסדרות]], יש ל<math>x_n</math> תת סדרה מתכנסת <math>x_{n_k}</math> (כיוון שהקטע סופי, הסדרה חסומה). | ||
| + | |||
| + | בנוסף, לתת הסדרה <math>y_{n_k}</math> יש תת סדרה מתכנסת. אם כך, בנינו זוג סדרות '''מתכנסות''' המקיימות את התנאים: | ||
| + | |||
| + | ::<math>x'_n-y'_n\rightarrow 0</math> | ||
| + | |||
| + | ::<math>|f(x'_n)-f(y'_n)|\geq \epsilon</math> | ||
| + | |||
| + | |||
| + | אבל '''כיוון שזה קטע סגור''', נקודת הגבול של הסדרות המתכנסות שייכת לקטע (נקודת הגבול בינהן זהה כי המרחק בינהן שואף לאפס). לכן, לפי רציפות, | ||
| + | |||
| + | ::<math>\lim f(x'_n)=\lim f(y'_n)</math> | ||
| + | |||
| + | בסתירה. | ||
גרסה מ־10:47, 10 בינואר 2012
חזרה למשפטים באינפי
משפט קנטור לגבי פונקציות רציפות במ"ש
פונקציה רציפה בקטע סגור וסופי, רציפה שם במ"ש
הוכחה
תהי f רציפה על קטע סגור וסופי ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נניח בשלילה שהיא לא רציפה שם במ"ש. לכן קיים אפסילון גדול מאפס, כך שלכל דלתא גדול מאפס, יש שתי נקודות במרחק קטן מדלתא כך שהפרש התמונות שלהן גדול או שווה לאפסילון. ניתן אם כך לבנות סדרה של זוגות של נקודות
. נניח בשלילה שהיא לא רציפה שם במ"ש. לכן קיים אפסילון גדול מאפס, כך שלכל דלתא גדול מאפס, יש שתי נקודות במרחק קטן מדלתא כך שהפרש התמונות שלהן גדול או שווה לאפסילון. ניתן אם כך לבנות סדרה של זוגות של נקודות
כך שמתקיים
אבל
לפי משפט בולצאנו-ויירשטראס לסדרות, יש ל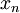 תת סדרה מתכנסת
תת סדרה מתכנסת 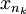 (כיוון שהקטע סופי, הסדרה חסומה).
(כיוון שהקטע סופי, הסדרה חסומה).
בנוסף, לתת הסדרה 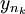 יש תת סדרה מתכנסת. אם כך, בנינו זוג סדרות מתכנסות המקיימות את התנאים:
יש תת סדרה מתכנסת. אם כך, בנינו זוג סדרות מתכנסות המקיימות את התנאים:
אבל כיוון שזה קטע סגור, נקודת הגבול של הסדרות המתכנסות שייכת לקטע (נקודת הגבול בינהן זהה כי המרחק בינהן שואף לאפס). לכן, לפי רציפות,
בסתירה.