הבדלים בין גרסאות בדף "משפט רול"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) |
|||
| (3 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
==משפט רול== | ==משפט רול== | ||
| + | תהי <math>f</math> פונקציה רציפה בקטע <math>[a,b]</math> וגזירה בקטע <math>(a,b)</math> כך ש- <math>f(a)=f(b)</math> . | ||
| − | + | אזי קיימת נקודה <math>c\in (a,b)</math> עבורה מתקיים <math>f'(c)=0</math> . | |
| − | + | ===הוכחה=== | |
| + | נוכיח כי קיימת נקודת קיצון מקומית <math>c\in (a,b)</math> ולכן המשל נובע [[משפט פרמה (אינפי)|ממשפט פרמה]]. | ||
| + | לפי משפט ויירשטראס השני, כיון שהפונקציה רציפה בקטע סגור היא מקבלת בו מינימום ומקסימום. | ||
| − | + | נחלק לשני מקרים: נניח המינימום וגם המקסימום מתקבלים בקצות הקטע <math>[a,b]</math> . על כן, כיון ש- <math>f(a)=f(b)</math> אנו מקבלים כי המקסימום והמינימום שווים ולכן הפונקציה קבועה בקטע. לכן כל נקודה בקטע היא נקודת קיצון מקומית, וקיבלנו את התוצאה הדרושה. | |
| − | + | ||
| − | + | ||
| − | + | ||
אחרת, המינימום או המקסימום מתקבלים בקטע הפתוח <math>(a,b)</math> ולכן הן נקודות קיצון מקומיות, ושוב קיבלנו את התוצאה הדרושה. | אחרת, המינימום או המקסימום מתקבלים בקטע הפתוח <math>(a,b)</math> ולכן הן נקודות קיצון מקומיות, ושוב קיבלנו את התוצאה הדרושה. | ||
| − | + | ==ראו גם== | |
| − | == ראו גם == | + | *[[משפט פרמה (אינפי)|משפט פרמה]] |
| − | + | *[[משפט לגראנז' (אינפי)|משפט לגראנז']] | |
| − | * [[משפט פרמה (אינפי)|משפט פרמה]] | + | |
| − | * [[משפט לגראנז' (אינפי)|משפט לגראנז']] | + | |
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
גרסה אחרונה מ־09:59, 13 באוקטובר 2016
משפט רול
תהי  פונקציה רציפה בקטע
פונקציה רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וגזירה בקטע
וגזירה בקטע 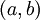 כך ש-
כך ש- 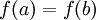 .
.
אזי קיימת נקודה 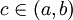 עבורה מתקיים
עבורה מתקיים 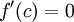 .
.
הוכחה
נוכיח כי קיימת נקודת קיצון מקומית 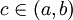 ולכן המשל נובע ממשפט פרמה.
ולכן המשל נובע ממשפט פרמה.
לפי משפט ויירשטראס השני, כיון שהפונקציה רציפה בקטע סגור היא מקבלת בו מינימום ומקסימום.
נחלק לשני מקרים: נניח המינימום וגם המקסימום מתקבלים בקצות הקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . על כן, כיון ש-
. על כן, כיון ש- 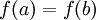 אנו מקבלים כי המקסימום והמינימום שווים ולכן הפונקציה קבועה בקטע. לכן כל נקודה בקטע היא נקודת קיצון מקומית, וקיבלנו את התוצאה הדרושה.
אנו מקבלים כי המקסימום והמינימום שווים ולכן הפונקציה קבועה בקטע. לכן כל נקודה בקטע היא נקודת קיצון מקומית, וקיבלנו את התוצאה הדרושה.
אחרת, המינימום או המקסימום מתקבלים בקטע הפתוח 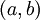 ולכן הן נקודות קיצון מקומיות, ושוב קיבלנו את התוצאה הדרושה.
ולכן הן נקודות קיצון מקומיות, ושוב קיבלנו את התוצאה הדרושה.