משתמש:אור שחף/133 - הרצאה/1.5.11
את משפט 10 לא סיימנו בשיעור הקודם ולכן השלמנו זאת ב־1.5.11. חלק זה מופיע בסיכום השיעור הקודם ולא בדף הנוכחי.
תוכן עניינים
אינטגרל לא אמיתי, סוג I (המשך)
תזכורת: עד כאן דיברנו רק על אינטגרלים מהסוג 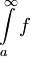 . כמובן שיש מקבילה גמורה לאינטגרלים האלה:
. כמובן שיש מקבילה גמורה לאינטגרלים האלה: 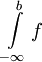 , ושאפשר לתרגם את כל המשפטים שלנו למקרה זה.
, ושאפשר לתרגם את כל המשפטים שלנו למקרה זה.
הגדרה: תהי f מוגדרת בכל 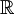 . נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית בכל קטע סופי
. נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית בכל קטע סופי ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . למשל, אם f רציפה למקוטעין ב-
. למשל, אם f רציפה למקוטעין ב-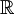 אז היא אינטגרבילית מקומית.
אז היא אינטגרבילית מקומית.
תזכורת: תהי f מוגדרת ואינטגרבילית מקומית. הגדרנו 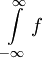 להיות
להיות 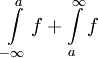 בתנאי ששני האינטגרלים התכנסים. אם אפילו אחד מהם מתבדר נאמר ש-
בתנאי ששני האינטגרלים התכנסים. אם אפילו אחד מהם מתבדר נאמר ש-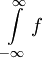 מתבדר. נבדוק שההגדרה בלתי תלוייה ב-a. ובכן בה"כ נבחר
מתבדר. נבדוק שההגדרה בלתי תלוייה ב-a. ובכן בה"כ נבחר 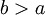 ונבדוק את שתי הטענות הבאות:
ונבדוק את שתי הטענות הבאות:
- שני האינטגרלים
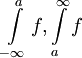 מתכנסים אם"ם שני האינטגרלים
מתכנסים אם"ם שני האינטגרלים 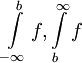 מתכנסים.
מתכנסים.
- עפ"י משפט 2,
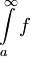 מתכנס אם"ם
מתכנס אם"ם 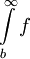 מתכנס. באותו אופן
מתכנס. באותו אופן 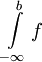 מתכנס אם"ם
מתכנס אם"ם 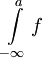 מתכנס, לכן הטענה מתקיימת.
מתכנס, לכן הטענה מתקיימת.
- עפ"י משפט 2,
- נוכיח שבמקרה שהאינטגרלים
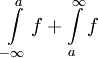 מתכנסים אז הם שווים ל-
מתכנסים אז הם שווים ל-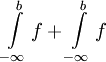 .
.
- ובכן עפ"י משפט 2,
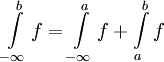 וגם
וגם 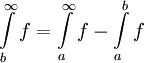 . נחבר את התוצאות ונקבל את הטענה.
. נחבר את התוצאות ונקבל את הטענה.
- ובכן עפ"י משפט 2,
אינטגרל לא אמיתי, סוג II
מדובר באינטגרל על קטע סגור של פונקציה לא חסומה.
הגדרה: תהי f מוגדרת בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . נאמר ש-f אינטגרבילית מקומית בקטע זה אם לכל c כך ש-
. נאמר ש-f אינטגרבילית מקומית בקטע זה אם לכל c כך ש-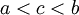 f אינטגרבילית בקטע
f אינטגרבילית בקטע ![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) (למשל, אם f רציפה למקוטעין ב-
(למשל, אם f רציפה למקוטעין ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) ). לכן נגדיר
). לכן נגדיר 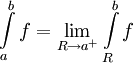 אם הגבול קיים. אם כן אומרים שהאינטגרל
אם הגבול קיים. אם כן אומרים שהאינטגרל  מתכנס או ש-f אינטגרבילית בקטע
מתכנס או ש-f אינטגרבילית בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אם אין גבול אומרים ש-
. אם אין גבול אומרים ש- מתבדר.
מתבדר.
דוגמאות
- נקח
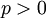 ונתבונן באינטגרל הלא אמיתי
ונתבונן באינטגרל הלא אמיתי 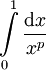 . עבור
. עבור 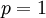 נקבל
נקבל ![\lim_{R\to0^+}\int\limits_R^1\frac{\mathrm dx}x=\lim_{R\to0^+}[\ln|x|]_{x=R}^1=\lim_{R\to0^+}-\ln(R)=\infty](/images/math/8/4/f/84f0f5b33d7cac024684511ba00aacf9.png) והאינטגרל מתבדר. עבור
והאינטגרל מתבדר. עבור 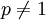 נקבל
נקבל ![\lim_{R\to0^+}\int\limits_R^1\frac{\mathrm dx}{x^p}=\lim_{R\to0^+}\left[\frac{x^{-p+1}}{-p+1}\right]_{x=R}^1=\lim_{R\to0^+}\frac1{1-p}-\frac{R^{-p+1}}{-p+1}=\begin{cases}\frac1{1-p}&p<1\\\infty&\text{else}\end{cases}](/images/math/b/b/4/bb4e14f5edcdeff1f83cdb03b0a23d6b.png) .
. -
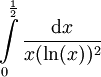 . נציב
. נציב 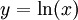 וכן
וכן 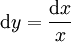 לקבל
לקבל 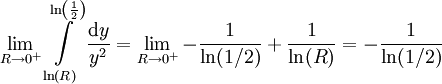 , ובפרט מתכנס.
, ובפרט מתכנס. - דרך כתיבה מקוצרת:
![\int\limits_0^1\frac{\mathrm dx}{\sqrt x}=\int\limits_0^1 x^{-\frac12}\mathrm dx=\left[\frac{x^{1/2}}{1/2}\right]_{x=0}^1=2](/images/math/8/e/8/8e823ef98f103798fd143c7935c8698b.png) .
.
לגבי משפטי התכנסות יש אנלוגיות למשפטים שהוכחנו עבור אינטגרל לא אמיתי מסוג ראשון. נרשום אותם ללא הוכחה.
הנחה קבועה: למעט במשפטים 1,3 הפונקציות f,g אינטגרביליות מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) .
.
משפט 1
אם f ו-g אינטגרביליות ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) ואם c קבוע אז
ואם c קבוע אז 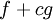 אינטגרבילית בקטע
אינטגרבילית בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) ומתקיים
ומתקיים 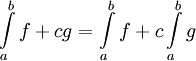 .
.
משפט 2
עבור 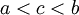 f אינטגרבילית בקטע
f אינטגרבילית בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) אם"ם היא אינטגרבילית בקטע
אם"ם היא אינטגרבילית בקטע ![(a,c]](/images/math/0/4/2/0425cdec60417e93bfbb1720291ef9f4.png) ואם כן
ואם כן 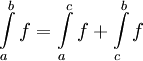 .
.
משפט 3
תהי f מוגדרת ומונוטונית בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אזי
. אזי 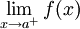 קיים אם"ם f חסומה בקטע
קיים אם"ם f חסומה בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) .
.
משפט 4
אם 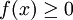 אז האינטגרל
אז האינטגרל  מתכנס אם"ם האינטגרלים החלקיים
מתכנס אם"ם האינטגרלים החלקיים 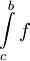 חסומים כאשר
חסומים כאשר 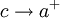 .
.
משפט 5 (מבחן ההשוואה)
נניח שב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) מתקיים
מתקיים 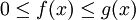 .
.
- אם
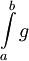 מתכנס אז
מתכנס אז  מתכנס.
מתכנס. - אם
 מתבדר אז
מתבדר אז 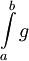 מתבדר.
מתבדר.
את ההמשך עשינו בשיעור שאחריו:
משפט 6 (מבחן ההשוואה הגבולי)
נניח ש-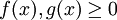 ונניח שקיים ממש
ונניח שקיים ממש 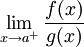 . אם
. אם 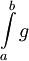 מתכנס אז
מתכנס אז  מתכנס.
מתכנס.
מסקנה
אם בפרט 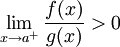 אז
אז 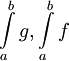 מתכנסים ומתבדרים יחדיו.
מתכנסים ומתבדרים יחדיו.
משפט 7
האינטגרל  מתכנס אם"ם הוא מקיים את תנאי קושי:
מתכנס אם"ם הוא מקיים את תנאי קושי: 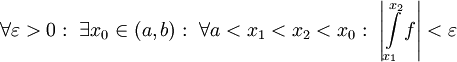
משפט 8
אם  מתכנס בהחלט אז
מתכנס בהחלט אז  מתכנס.
מתכנס.
באופן דומה יש אנלוגיות לכל המשפטים האלה עבור קטעים מהצורה 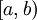 (ז"א הפונקציה לא חסומה בסביבת b במקום בסביבת a. במקרה כזה מגדירים
(ז"א הפונקציה לא חסומה בסביבת b במקום בסביבת a. במקרה כזה מגדירים 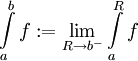 ). כמו כן, אם f מוגדרת ב-
). כמו כן, אם f מוגדרת ב-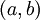 ולא חסומה בסביבת שני הקצוות מגדירים
ולא חסומה בסביבת שני הקצוות מגדירים 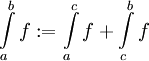 עבור
עבור 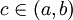 כלשהו ונאמר ש-
כלשהו ונאמר ש- מתכנס אם"ם שני האינטגרלים
מתכנס אם"ם שני האינטגרלים 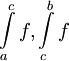 מתכנסים.
מתכנסים.
אם f מוגדרת ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) למעט איזו נקודת בייניים
למעט איזו נקודת בייניים 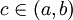 שסביבה f אינה חסומה, אז נגדיר
שסביבה f אינה חסומה, אז נגדיר 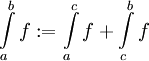 כך ששני האינטגרלים באגף ימין מתכנסים.
כך ששני האינטגרלים באגף ימין מתכנסים.