משתמש:אור שחף/133 - הרצאה/27.2.11
תוכן עניינים
האינטגרל לפי דרבו (המשך)
משפט 8
נניח ש-f מוגדרת וחסומה בקטע ![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png) ונניח ש-
ונניח ש-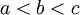 . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וב-
וב-![[b,c]](/images/math/2/3/8/238bb374974bd3b5bf3b51c245fb1bdc.png) אם"ם היא אינטגרבילית ב-
אם"ם היא אינטגרבילית ב-![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png) , ואם כן מתקיים
, ואם כן מתקיים 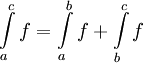 .
.
הוכחה
 : נתונה f אינטגרבילית ב-
: נתונה f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וב-
וב-![[b,c]](/images/math/2/3/8/238bb374974bd3b5bf3b51c245fb1bdc.png) . נקח חלוקה כלשהי P של
. נקח חלוקה כלשהי P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וחלוקה Q של
וחלוקה Q של ![[b,c]](/images/math/2/3/8/238bb374974bd3b5bf3b51c245fb1bdc.png) ונגדיר
ונגדיר 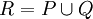 (כלומר R חלוקה של
(כלומר R חלוקה של ![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png) ). לכן מתקיים
). לכן מתקיים 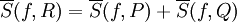 . נשאיף
. נשאיף 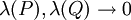 . לפי הנתון
. לפי הנתון 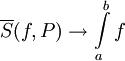 וגם
וגם 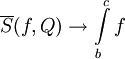 , לכן
, לכן 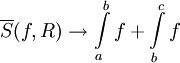 . באותו אופן נקבל
. באותו אופן נקבל 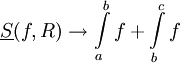 . הראנו ש-
. הראנו ש-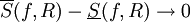 ולכן f אינטגרבילית ב-
ולכן f אינטגרבילית ב-![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png) . ע"פ משפט 4 נסיק
. ע"פ משפט 4 נסיק 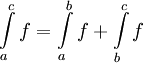 .
.
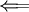 : נבחר חלוקות P,Q,R כמו בחלק הקודם, ושוב
: נבחר חלוקות P,Q,R כמו בחלק הקודם, ושוב 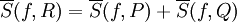 ו-
ו-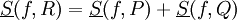 . נחסיר ונקבל:
. נחסיר ונקבל: 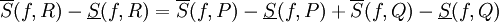 . כעת, אם
. כעת, אם  , האינטגרביליות של f על
, האינטגרביליות של f על ![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png) גוררת שעבור
גוררת שעבור 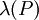 ו-
ו-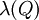 מספיק קטנים
מספיק קטנים 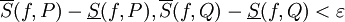 . קיום חלוקה P כזאת לכל
. קיום חלוקה P כזאת לכל  מוכיח ש-f אינטגרבילית ב-
מוכיח ש-f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וקיום חלוקה Q - ב-
וקיום חלוקה Q - ב-![[b,c]](/images/math/2/3/8/238bb374974bd3b5bf3b51c245fb1bdc.png) . השיוויון
. השיוויון 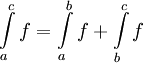 נובע מהחלק הקודם.
נובע מהחלק הקודם. 
הכללה
אם 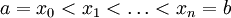 ואם f אינטגרבילית ב-
ואם f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 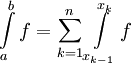 . ההוכחה באינדוקציה.
. ההוכחה באינדוקציה.
מוסכמות:
-
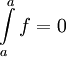
- אם
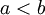 ואם f אינטגרבילית ב-
ואם f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נרשום
נרשום 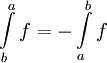
(אלה מוסכמות ולא משפטים כי באופן שבו הגדרנו את האינטגרל עד עכשיו, 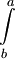 לא מוגדר עבור
לא מוגדר עבור 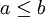 )
)
עם מוסכמות אלה יתקיים:
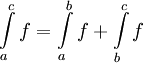 באופן בלתי תלוי בסדר של המספרים a,b,c. למשל, אם
באופן בלתי תלוי בסדר של המספרים a,b,c. למשל, אם 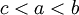 אז לפי משפט 8
אז לפי משפט 8 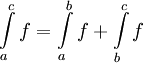 . נבדוק:
. נבדוק: 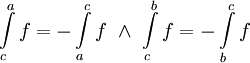 ולכן
ולכן 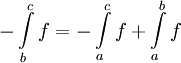 , מה שגורר
, מה שגורר 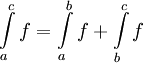 .
.
משפט 9
תהי f מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . עוד נניח ש-f רציפה ב-
. עוד נניח ש-f רציפה ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
יהי נתון. נגדיר
נתון. נגדיר 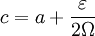 . לפי הנתון f רציפה ב-
. לפי הנתון f רציפה ב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) , אזי ממשפט 6 היא אינטגרבילית ב-
, אזי ממשפט 6 היא אינטגרבילית ב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) , לכן נוכל לבחור חלוקה P של
, לכן נוכל לבחור חלוקה P של ![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) כך ש-
כך ש-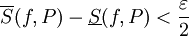 . כעת נגדיר חלוקה Q של
. כעת נגדיר חלוקה Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ע"י
ע"י 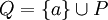 . עוד נגדיר
. עוד נגדיר 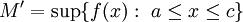 וכן
וכן 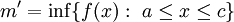 . נובע כי
. נובע כי 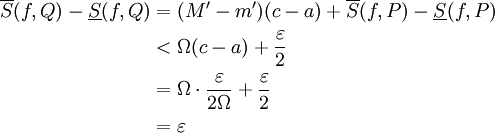
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 
מסקנה 1
המשפט נכון אם f חסומה ורציפה ב-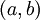 .
.
מסקנה 2
נניח ש-f חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ורציפה שם פרט למספר סופי של נקודות
ורציפה שם פרט למספר סופי של נקודות 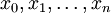 כך ש-
כך ש-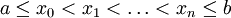 . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
עבור כל k נקבל ש-f חסומה ב-![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) ורציפה ב-
ורציפה ב-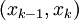 . לפי מסקנה 1, f אינטגרבילית ב-
. לפי מסקנה 1, f אינטגרבילית ב-![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) . נסתמך על ההכללה למשפט 8 לומר ש-f אינטגרבילית ב-
. נסתמך על ההכללה למשפט 8 לומר ש-f אינטגרבילית ב-![[a,b]=\bigcup_{k=1}^n [x_{k-1},x_k]](/images/math/8/0/d/80d3c82e91b924c56d753760172fe8d6.png) .
. 
הגדרה: אומרים ש-f "רציפה למקוטעין" ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון.
אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון.
נובע ממסקנה 2 שכל פונקציה רציפה למקוטעין ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אינטגרבילית שם. באופן דומה אפשר להוכיח שאם f מוגדרת ו"מונוטונית למקוטעין" ב-
אינטגרבילית שם. באופן דומה אפשר להוכיח שאם f מוגדרת ו"מונוטונית למקוטעין" ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז היא אינטגרבילית שם.
אז היא אינטגרבילית שם.
האינטגרל לפי רימן
הקדמה - הגישה של רימן
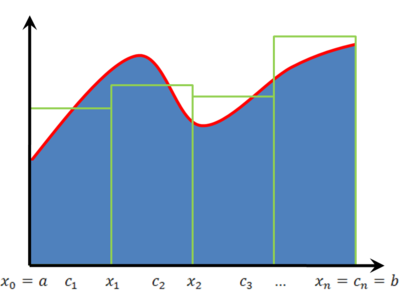
נניח ש-f מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נבחר חלוקה P של
. נבחר חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: 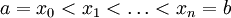 . עוד נבחר לכל k מספר
. עוד נבחר לכל k מספר ![c_k\in[x_{k-1},x_k]](/images/math/c/b/b/cbbb2a7a61cd7e98c21895f0cabd6417.png) ונכנה כ-P' את התת חלוקה
ונכנה כ-P' את התת חלוקה 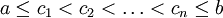 . ז"א
. ז"א 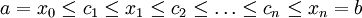 . בהתאם לכך נבנה סכום רימן
. בהתאם לכך נבנה סכום רימן 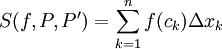 כאשר לכל k מתקיים
כאשר לכל k מתקיים 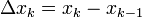 .
.
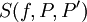 מקרב את השטח שמתחת לגרף, אך לא ידוע אם הוא גדול, קטן או שווה לו.
מקרב את השטח שמתחת לגרף, אך לא ידוע אם הוא גדול, קטן או שווה לו.
נעיר שעל חלוקה אחת P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אפשר לבנות אינסוף סכומי רימן
אפשר לבנות אינסוף סכומי רימן 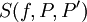 . עם זאת, יתקיים תמיד
. עם זאת, יתקיים תמיד 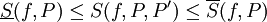 . יתר על כן,
. יתר על כן, 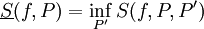 ו-
ו-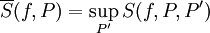 .
.
הגדרת האינטגרל לפי רימן: תהי f מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נאמר ש-f אינטגרבילית ב-
. נאמר ש-f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם כאשר
אם כאשר 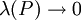 כל סכומי רימן
כל סכומי רימן 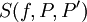 שואפים לגבול אחד, שיסומן
שואפים לגבול אחד, שיסומן  .
.
משפט 10
תהי f מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי f אינטגרבילית שם לפי רימן אם"ם f אינטגרבילית שם לפי דרבו, ואם כן אז
. אזי f אינטגרבילית שם לפי רימן אם"ם f אינטגרבילית שם לפי דרבו, ואם כן אז 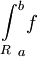 (לפי רימן)
(לפי רימן) 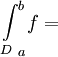 (לפי דרבו).
(לפי דרבו).
הוכחה
תחילה נניח ש-f אינטגרבילית לפי דרבו. נעיר שלכל חלוקה P ותת חלוקה P' של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
:
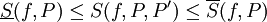 . כעת נשאיף
. כעת נשאיף 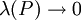 . כיוון ש-f אינטגרבילית דרבו,
. כיוון ש-f אינטגרבילית דרבו, 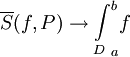 וכן
וכן 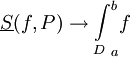 לכן משפט הסנדויץ' מבטיח ש-
לכן משפט הסנדויץ' מבטיח ש-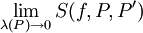 קיים ושווה ל-
קיים ושווה ל-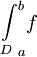 . ז"א f אינטגרבילית רימן ומתקיים
. ז"א f אינטגרבילית רימן ומתקיים 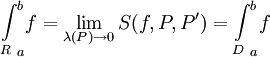 .
.
לצד השני, נניח ש-f אינטגרבילית רימן. אזי מתקיים 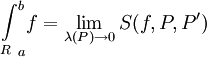 . אם כן הוא גם שווה ל-
. אם כן הוא גם שווה ל-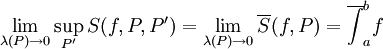 ,ובאופן דומה עבור אינטגרל תחתון (לפי דרבו, כמובן). מצאנו
,ובאופן דומה עבור אינטגרל תחתון (לפי דרבו, כמובן). מצאנו 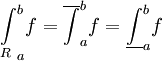 . עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם הוכחנו ש-
. עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם הוכחנו ש-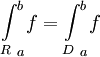 .
. 
משפט 11 (תכונות האינטגרל)
נניח ש-f ו-g מוגדרות ואינטגרביליות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ונניח ש-c קבוע כלשהו. אזי:
, ונניח ש-c קבוע כלשהו. אזי:
- (לינאריות):
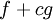 אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ומתקיים
ומתקיים 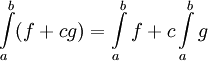 .
. - (מונוטוניות): אם
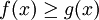 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) אז
אז 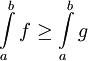 . (חיוביות): בפרט, אם
. (חיוביות): בפרט, אם ![\forall x\in[a,b]:\ f(x)\ge0](/images/math/2/8/6/286bfa2f0ea6e33a9691152f7160ba89.png) אז
אז 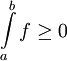 .
. - (הכללה לאי-שיוויון המשולש): |f| אינטגרבילית ב-
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וגם
וגם 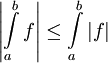 .
. - אם
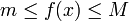 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 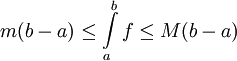 ואם
ואם 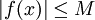 בקטע זה אז אז
בקטע זה אז אז 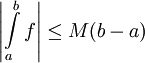 .
. - אם
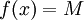 (פונקציה קבועה) אז
(פונקציה קבועה) אז 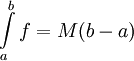 .
.
הוכחה
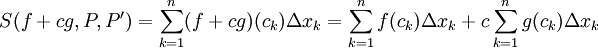 . נשאיף
. נשאיף 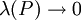 . כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א
. כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א 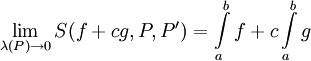 . עצם קיום הגבול אומר ש-
. עצם קיום הגבול אומר ש-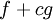 אינטגרבילית ולפי ערך הגבול נסיק
אינטגרבילית ולפי ערך הגבול נסיק 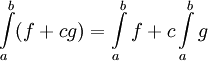 .
. 
את ההמשך עשינו בשיעור שאחריו:
- נתבונן בסכום רימן כלשהו עבור g:
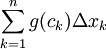 . לפי הנתון הוא קטן או שווה ל-
. לפי הנתון הוא קטן או שווה ל- 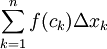 . נשאיף
. נשאיף 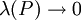 . סכומים אלה שואפים לאינטגרלים של f ו-g ונסיק
. סכומים אלה שואפים לאינטגרלים של f ו-g ונסיק 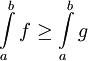 .
. 
- נעיר ש-
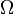 היא בעצם
היא בעצם ![\Omega(f)=\sup\{|f(x)-f(y)|:\ x,y\in[a,b]\}](/images/math/d/5/5/d55228526171b8599af0542a0d8414c0.png) . כזכור, אי שיוויון המשולש גורר ש-
. כזכור, אי שיוויון המשולש גורר ש-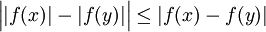 . לכן
. לכן ![\Omega(|f|)=\sup_{x,y\in[a,b]}\Big||f(x)|-|f(y)|\Big|\le\sup_{x,y\in[a,b]}|f(x)-f(y)|=\Omega(f)](/images/math/2/1/1/211c5c4e01f8709b2e1d106f0077d183.png) . כעת תהי P חלוקה כלשהי של
. כעת תהי P חלוקה כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ואז
ואז 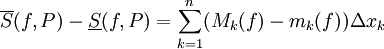 . נעיר שלכל f,
. נעיר שלכל f, 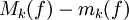 היא התנודה של f בקטע
היא התנודה של f בקטע ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) ולפי מה שהוכחנו זה גדול או שווה לתנודה של |f| באותו קטע: כעת נוכיח ש-|f| אינטגרבילית. לצורך זה יהי
ולפי מה שהוכחנו זה גדול או שווה לתנודה של |f| באותו קטע: כעת נוכיח ש-|f| אינטגרבילית. לצורך זה יהי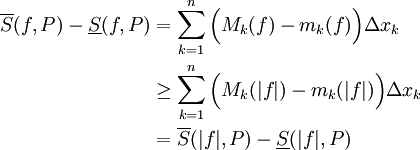
 נתון. כיוון ש-f אינטגרבילית (נתון) קיימת חלוקה P של
נתון. כיוון ש-f אינטגרבילית (נתון) קיימת חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-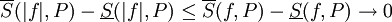 ונובע ממשפט 5 ש-|f| אינטגרבילית. נותר להוכיח את אי-השיוויון
ונובע ממשפט 5 ש-|f| אינטגרבילית. נותר להוכיח את אי-השיוויון 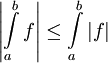 . לפי אי-שיוויון המשולש, לכל סכום רימן של f מתקיים
. לפי אי-שיוויון המשולש, לכל סכום רימן של f מתקיים 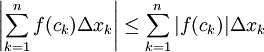 . נשאיף
. נשאיף 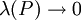 ונקבל ש-
ונקבל ש-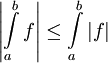 .
. 
- נתון
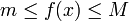 . לפי משפט 1, לכל חלוקה P של
. לפי משפט 1, לכל חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) מתקיים
מתקיים 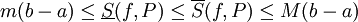 . נשאיף את
. נשאיף את 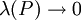 כדי להסיק
כדי להסיק 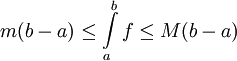 . אם נתון
. אם נתון 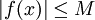 אז נוכל להסתמך על סעיף 3 ומה שהוכחנו הרגע לומר
אז נוכל להסתמך על סעיף 3 ומה שהוכחנו הרגע לומר 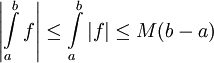 .
. 
- לפי הנתון
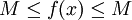 . לכן, עפ"י סעיף 4
. לכן, עפ"י סעיף 4 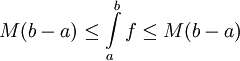 ויש שיוויון.
ויש שיוויון.