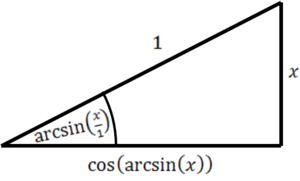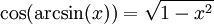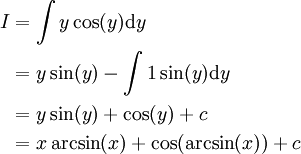משתמש:אור שחף/133 - הרצאה/6.3.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
תוכן עניינים
האינטגרל הלא מסויים
הגדרה: אינטגרל מסויים הוא אינטגרל עם גבולות  שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות -
שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות - 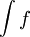 , שפתרונו פשוט
, שפתרונו פשוט 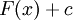 עבור F פונקציה קדומה ל-f וקבוע c.
עבור F פונקציה קדומה ל-f וקבוע c.
אינטגרלים פשוטים
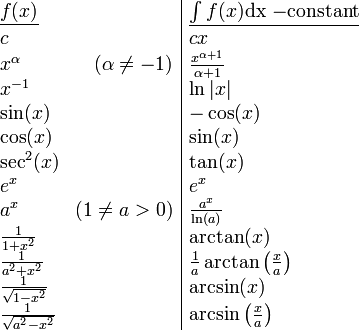
בדיקות
- נבדוק
 (עבור
(עבור  ): לפי ההגדרה
): לפי ההגדרה 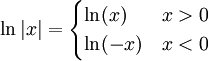 . לכן עבור
. לכן עבור 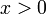 מתקיים
מתקיים
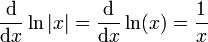 ועבור
ועבור 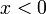 ,
, 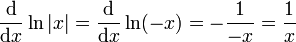 .
. 
-
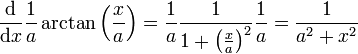 .
. 
-
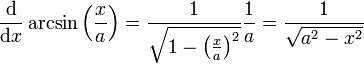 .
. 
דוגמאות חישוב
-
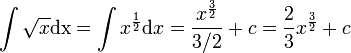
-
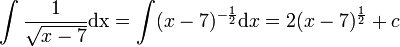
-
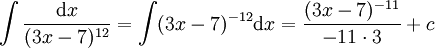 (מהפיכת כלל השרשרת)
(מהפיכת כלל השרשרת) -
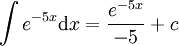
-
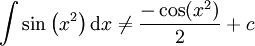 (למעשה, האינטגרל הזה לא אלמנטרי)
(למעשה, האינטגרל הזה לא אלמנטרי) -
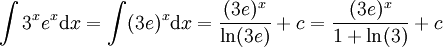
-
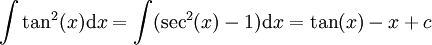
-
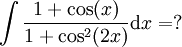 (הפונקציה אלמנטרית אבל האינטגרל לא ידוע לנו. המסר הוא שהאינטגרציה קשה)
(הפונקציה אלמנטרית אבל האינטגרל לא ידוע לנו. המסר הוא שהאינטגרציה קשה) -
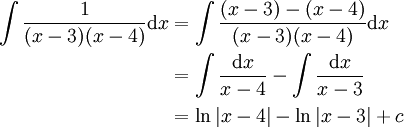
כלל פשוט: האינטגרל לינארי, כלומר 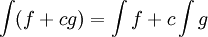 .
.
אינטגרציה בחלקים
כזכור, אם f ו-g פונקציות גזירות אז 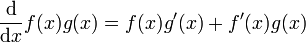 . אם f' ו-g' רציפות נוכל להפוך את זה לנוסחת אינטגרציה:
. אם f' ו-g' רציפות נוכל להפוך את זה לנוסחת אינטגרציה:
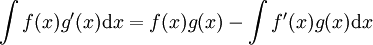 .
.
דוגמאות חישוב
-
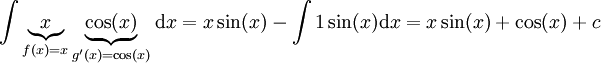 . אם ננסה לפתור אינטגרל זה בדרך הפוכה נקבל
. אם ננסה לפתור אינטגרל זה בדרך הפוכה נקבל 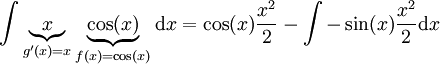 , ואינטגרל זה יותר קשה מהאינטגרל המקורי.
, ואינטגרל זה יותר קשה מהאינטגרל המקורי. -
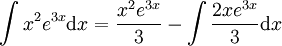 . נעשה שוב אינטגרציה בחלקים:
. נעשה שוב אינטגרציה בחלקים: 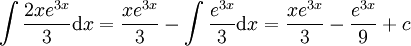 ובסה"כ
ובסה"כ 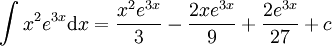 .
. -
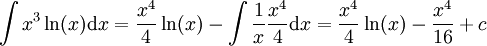 .
. -
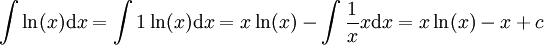 .
. -
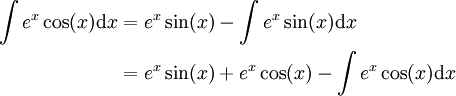 ולכן
ולכן 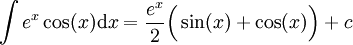 .
.
שיטת ההצבה/שינוי משתנים
נתחיל עם כלל השרשרת: 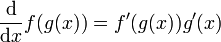 . לכן אם F קדומה ל-f אז
. לכן אם F קדומה ל-f אז 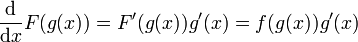 ולפיכך
ולפיכך 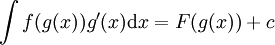 .
.
דרך פורמלית וכללית לפתרון: נתון 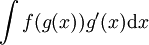 . ע"י הגדרה
. ע"י הגדרה 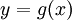 נקבל
נקבל 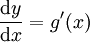 . נעביר אגף:
. נעביר אגף: 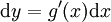 , נחזור לאינטגרל ונקבל
, נחזור לאינטגרל ונקבל 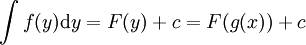 .
.
דוגמאות חישוב
בכל אחת מהדוגמאות הבאות נסמן את האינטגרל שיש לחשב כ-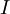 :
:
-
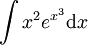 : נציב
: נציב 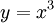 ולכן
ולכן 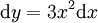 ולפיכך
ולפיכך 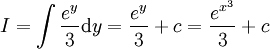 .
. -
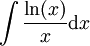 : נציב
: נציב 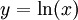 ואז
ואז 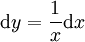 ונובע ש-
ונובע ש-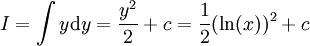 .
. -
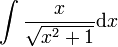 : נציב
: נציב 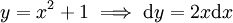 ולכן
ולכן 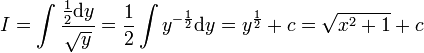 .
. -
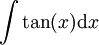 : עבור
: עבור 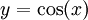 נקבל
נקבל 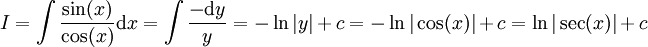 .
. -
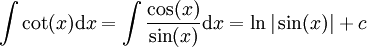 .
. 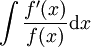 : נציב
: נציב 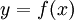 ונקבל
ונקבל 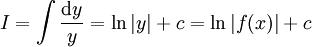 .
.
לכן ניתן להוכיח שוב את סעיף 4: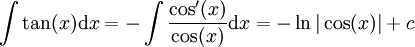 .
.-
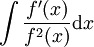 : נציב
: נציב 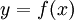 ונקבל
ונקבל 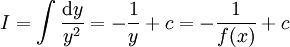 .
. -
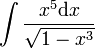 : נציב
: נציב 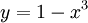 ואז
ואז 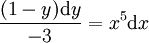 . מכאן ש-
. מכאן ש-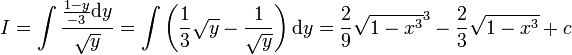 .
. -
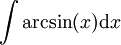 : נציב
: נציב 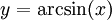 ומכאן ש-
ומכאן ש-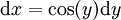 . לבסוף, ולכן
. לבסוף, ולכן 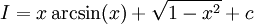 .
.
דרך אחרת: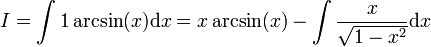 . נגדיר
. נגדיר 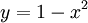 ושוב נקבל
ושוב נקבל 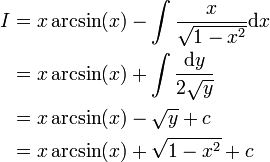
-
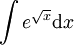 : נציב
: נציב 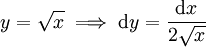 ולכן
ולכן 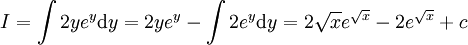 .
. -
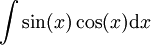 : נבחר
: נבחר 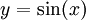 כדי לקבל
כדי לקבל 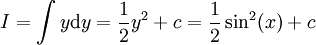 .
.
שיטה אחרת: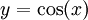 ואז
ואז 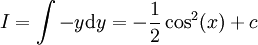 .
.
שיטה אחרונה: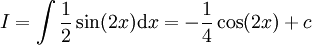 .
.
קיבלנו 3 תשובות שונות באותו תרגיל, אך אין סתירה כי ההפרש בין כל שתי תשובות הוא גודל קבוע. למשל: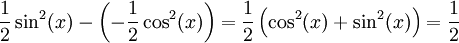 .
.