הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/22.5.11"
מ (←מבחן ה-M של ווירשטראס) |
|||
| שורה 1: | שורה 1: | ||
=התכנסות במ"ש {{הערה|(המשך)}}= | =התכנסות במ"ש {{הערה|(המשך)}}= | ||
==משפט דיני== | ==משפט דיני== | ||
| − | + | <math>f_n</math> סדרת פונקציות רציפה המוגדרת בקטע <math>[a,b]</math> ומתכנסת נקודתית בקטע זה לפונקציה רציפה f. בנוסף <math>\{f_n(x)\}</math> סדרה עולה לכל <math>x\in[a,b]</math>. אזי <math>f_n</math> מתכנסת במ"ש ב-<math>[a,b]</math>. | |
===דוגמה 1=== | ===דוגמה 1=== | ||
בדוק הכנסות עבור הסדרה <math>f_n(x)=\sqrt[n]{\sin(x)}</math> בקטע | בדוק הכנסות עבור הסדרה <math>f_n(x)=\sqrt[n]{\sin(x)}</math> בקטע | ||
| − | + | <ol><li><math>\left[\tfrac\pi4,\tfrac34\pi\right]</math> | |
====פתרון==== | ====פתרון==== | ||
| − | + | נשים לב שעבור x בקטע <math>\sin(x)>0</math>. קל לראות גם שפונקצית הגבול היא <math>\lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}\sqrt[n]{\sin(x)}=1</math>, שרציפה. כמו כן ברור כי <math>f_n</math> רציפות ובקטע מתקיים <math>\sqrt[n+1]{\sin(x)}\ge\sqrt[n]{\sin(x)}</math>. לכן מתקיימים תנאי משפט דיני, ומכאן שההתכנסות במ"ש. {{משל}}</li> | |
| − | + | <li><math>(0,\pi)</math> | |
====פתרון==== | ====פתרון==== | ||
| − | נשים לב שנתון קטע פתוח, לכן לא ניתן להשתמש בתנאי דיני. ברור לנו שפונקצית הגבול <math>f(x)=1</math> ומכיוון ש-<math>\sup_{x\in(0,\pi)}\left|1-\sqrt[n]{\sin(x)}\right|=1\ne0</math>. {{משל}} | + | נשים לב שנתון קטע פתוח, לכן לא ניתן להשתמש בתנאי דיני. ברור לנו שפונקצית הגבול <math>f(x)=1</math> ומכיוון ש-<math>\sup_{x\in(0,\pi)}\left|1-\sqrt[n]{\sin(x)}\right|=1\ne0</math> ההתכנסות אינה במ"ש. {{משל}} |
| + | </li></ol> | ||
==דוגמה 2== | ==דוגמה 2== | ||
| − | קבעו אם הטור <math>\sum_{n=1}^\infty x^{2n}</math> מתכנס ב-<math>\left[-\ | + | קבעו אם הטור <math>\sum_{n=1}^\infty x^{2n}</math> מתכנס ב-<math>\left[-\tfrac34,\tfrac34\right]</math>. |
===פתרון=== | ===פתרון=== | ||
| − | נשתמש | + | נשתמש בנוסחאת הסכום לטור הנדסי: <math>\sum_{n=1}^\infty x^{2n}=\sum_{n=1}^\infty \left(x^2\right)^n=\frac{x^2}{1-x^2}</math>. לכן יש התכנסות לפונקציה רציפה בקטע. ברור שאיברי הטור פונקציות רציפות ואי שליליות (ולכן מתקיימת מונוטוניות). לפי משפט דיני ההתכנסות במ"ש. {{משל}} |
| − | ==דוגמה 3 | + | ==דוגמה 3== |
הוכח או הפרך: אם <math>f_n:[a,b]\to[c,d]</math> סדרת פונקציות המתכנסת במ"ש לפונקצית הגבול f וכן <math>g:[c,d]\to\mathbb R</math> פונקציה רציפה אז <math>g\circ f_n</math> היא סדרת פונקציות המתכנסות במ"ש לפונקצית הגבול <math>g\circ f</math>. | הוכח או הפרך: אם <math>f_n:[a,b]\to[c,d]</math> סדרת פונקציות המתכנסת במ"ש לפונקצית הגבול f וכן <math>g:[c,d]\to\mathbb R</math> פונקציה רציפה אז <math>g\circ f_n</math> היא סדרת פונקציות המתכנסות במ"ש לפונקצית הגבול <math>g\circ f</math>. | ||
===פתרון=== | ===פתרון=== | ||
| − | נשים לב כי g רציפה בקטע סגור ולכן רציפה במ"ש. כלומר לכל <math>\varepsilon>0</math> יש <math>\delta>0</math> כך שאם <math>|y_1-y_2|<\delta</math> אז <math>|g(y_1)-g(y_2)|<\varepsilon</math>. בנוסף נתון ש-<math>f_n</math> מתכנסת במ"ש ולכן יש N כך שלכל <math>n>N</math> מתקיים <math>|f_n(x)-f(x)|<\delta</math> (בפרט אפשר לבחור <math>\varepsilon=\delta</math>. | + | נשים לב כי g רציפה בקטע סגור ולכן רציפה במ"ש. כלומר לכל <math>\varepsilon>0</math> יש <math>\delta>0</math> כך שאם <math>|y_1-y_2|<\delta</math> אז <math>|g(y_1)-g(y_2)|<\varepsilon</math>. בנוסף נתון ש-<math>f_n</math> מתכנסת במ"ש ולכן יש N כך שלכל <math>n>N</math> מתקיים <math>|f_n(x)-f(x)|<\delta</math> (בפרט אפשר לבחור <math>\varepsilon=\delta</math>). |
| − | נשים לב ש-<math>g\circ f_n</math> מוגדרת היטב | + | נשים לב ש-<math>g\circ f_n</math> מוגדרת היטב לכל <math>a\le x\le b</math> ועבור <math>n>N</math> מתקיים <math>|g(f_n(x))-g(f(x))|<\varepsilon</math>. מכאן ש-<math>g\circ f_n\to g\circ f</math> במ"ש. {{משל}} |
==מבחן ה-M של ווירשטראס== | ==מבחן ה-M של ווירשטראס== | ||
| שורה 25: | שורה 26: | ||
==דוגמה 4== | ==דוגמה 4== | ||
הוכח כי <math>\sum_{n=1}^\infty x^n(1-x)^n</math> מתכנס במ"ש ב-<math>[0,1]</math>. | הוכח כי <math>\sum_{n=1}^\infty x^n(1-x)^n</math> מתכנס במ"ש ב-<math>[0,1]</math>. | ||
| + | |||
===פתרון=== | ===פתרון=== | ||
| − | נרשום את הטור כ-<math>\sum_{n=1}^\infty (x(1-x))^n</math> נסמן <math>f(x)=x(1-x)</math> ונחסום אותה: <math>f(x)=x-x^2\implies f'(x)=1-2x</math> | + | נרשום את הטור כ-<math>\sum_{n=1}^\infty (x(1-x))^n</math> נסמן <math>f(x)=x(1-x)</math> ונחסום אותה: <math>f(x)=x-x^2\implies f'(x)=1-2x</math> ולכן <math>f'(x)=0\iff x=\frac12</math>, שהיא מקסימום כי <math>f''(1/2)=-2<0</math>. נותר לבדוק את קצוות הקטע: <math>f(0)=f(1)=0</math>. נסיק ש-<math>x=\frac12</math> היא נקודת קיצון גלובלית וכן-<math>f(1/2)=\frac14\implies f_n(x)=(x(1-x))^n\le\left(\frac14\right)^n</math>. <math>\sum_{n=1}^\infty\frac1{4^n}</math> מתכנס (זהו טור הנדסי) ולכן, לפי מבחן ה-M של וירשטרס, הטור <math>\sum_{n=1}^\infty x^n(1-x)^n</math> מתכנס במ"ש. {{משל}} |
| − | + | ||
| − | + | ==אינטגרציה איבר-איבר בסדרות== | |
| + | תהי <math>f_n</math> סדרת פונקציות רציפות המתכנסות במ"ש לפונקציות f בקטע I. אזי f אינטגרבילית בקטע ומתקיים <math>\lim_{n\to\infty}\int\limits_a^b f_n=\int\limits_a^b\lim_{n\to\infty}f_n=\int\limits_a^b f</math>. | ||
===דוגמה 5=== | ===דוגמה 5=== | ||
| − | קבע האם <math>\lim_{n\to\infty}\int\limits_0^1 f_n</math> מתכנס כאשר | + | קבע האם <math>\lim_{n\to\infty}\int\limits_0^1 f_n</math> מתכנס כאשר <math>f_n(x)=nxe^{-nx^2}</math> ב-<math>[0,1]</math>, והאם <math>f_n\to f</math> במ"ש. |
| + | ====פתרון==== | ||
| + | נציב <math>y=x^2</math> ואז <math>\int\limits_0^1 f_n=\frac n2\int\limits_0^1e^{-ny}\mathrm dy=\frac n2\left[\frac{e^{-ny}}{-n}\right]_{y=0}^1=-\frac12e^{-n}+\frac12\to\frac12</math>, כלומר <math>\lim_{n\to\infty}\int\limits_0^1 f_n</math> אכן מתכנס. נותר לבדוק אם <math>\{f_n\}</math> מתכנסת במ"ש: | ||
| + | ''דרך 1:'' <math>f(x)=\lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}\frac{nx}{e^{nx^2}}=0</math> (השיוויון האחרון לפי לופיטל). נניח בשלילה שההתכנסות במ"ש, אבל <math>\lim_{n\to\infty}\int\limits_0^1 nxe^{-nx^2}\mathrm dx=\frac12\ne 0=\int\limits_0^1 f</math> ולכן קיבלנו סתירה. לפיכך ההתכנסות אינה במ"ש. {{משל}} | ||
| − | + | ''דרך 2:'' הראנו כבר כי פונקצית הגבול היא 0. נחפש מקסימום ל-<math>f_n(x)</math>: <math>0=f_n'(x)=-2n^2x^2e^{-nx^2}+ne^{-nx^2}=ne^{-nx^2}(-2x^2n+1)</math> ונקבל <math>x=\frac1\sqrt{2n}</math>. לכן <math>\sup\left|f_n(x)-f(x)\right|=\frac n\sqrt{2n}e^{-\frac n{2n}}-0=\sqrt\frac n2e^{-\frac 1{2}}\to\infty\ne0</math> ומכאן שההתכנסות אינה במ"ש. {{משל}} | |
| − | + | ||
| − | + | ||
גרסה מ־14:14, 28 ביוני 2011
תוכן עניינים
התכנסות במ"ש (המשך)
משפט דיני
 סדרת פונקציות רציפה המוגדרת בקטע
סדרת פונקציות רציפה המוגדרת בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ומתכנסת נקודתית בקטע זה לפונקציה רציפה f. בנוסף
ומתכנסת נקודתית בקטע זה לפונקציה רציפה f. בנוסף 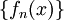 סדרה עולה לכל
סדרה עולה לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . אזי
. אזי  מתכנסת במ"ש ב-
מתכנסת במ"ש ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
דוגמה 1
בדוק הכנסות עבור הסדרה ![f_n(x)=\sqrt[n]{\sin(x)}](/images/math/6/1/5/615da40819a44ed7f00931c4a693c793.png) בקטע
בקטע
![\left[\tfrac\pi4,\tfrac34\pi\right]](/images/math/7/e/d/7ed79addfe9fd78f8d2fdc485c481801.png)
פתרון
נשים לב שעבור x בקטע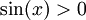 . קל לראות גם שפונקצית הגבול היא
. קל לראות גם שפונקצית הגבול היא ![\lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}\sqrt[n]{\sin(x)}=1](/images/math/e/9/f/e9fa75dca80bd3466f49d47d789843b1.png) , שרציפה. כמו כן ברור כי
, שרציפה. כמו כן ברור כי  רציפות ובקטע מתקיים
רציפות ובקטע מתקיים ![\sqrt[n+1]{\sin(x)}\ge\sqrt[n]{\sin(x)}](/images/math/2/c/3/2c3528b548e323548058668b8d613d35.png) . לכן מתקיימים תנאי משפט דיני, ומכאן שההתכנסות במ"ש.
. לכן מתקיימים תנאי משפט דיני, ומכאן שההתכנסות במ"ש. 
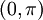
פתרון
נשים לב שנתון קטע פתוח, לכן לא ניתן להשתמש בתנאי דיני. ברור לנו שפונקצית הגבול
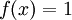 ומכיוון ש-
ומכיוון ש-![\sup_{x\in(0,\pi)}\left|1-\sqrt[n]{\sin(x)}\right|=1\ne0](/images/math/a/c/5/ac57619d7616844ec4df52447554b9ce.png) ההתכנסות אינה במ"ש.
ההתכנסות אינה במ"ש. 
דוגמה 2
קבעו אם הטור 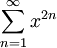 מתכנס ב-
מתכנס ב-![\left[-\tfrac34,\tfrac34\right]](/images/math/5/6/3/563bc3d4c74385f4de5fe276c9443916.png) .
.
פתרון
נשתמש בנוסחאת הסכום לטור הנדסי: 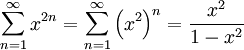 . לכן יש התכנסות לפונקציה רציפה בקטע. ברור שאיברי הטור פונקציות רציפות ואי שליליות (ולכן מתקיימת מונוטוניות). לפי משפט דיני ההתכנסות במ"ש.
. לכן יש התכנסות לפונקציה רציפה בקטע. ברור שאיברי הטור פונקציות רציפות ואי שליליות (ולכן מתקיימת מונוטוניות). לפי משפט דיני ההתכנסות במ"ש. 
דוגמה 3
הוכח או הפרך: אם ![f_n:[a,b]\to[c,d]](/images/math/4/a/9/4a9541b49b92a67090b89ac221d9bcd5.png) סדרת פונקציות המתכנסת במ"ש לפונקצית הגבול f וכן
סדרת פונקציות המתכנסת במ"ש לפונקצית הגבול f וכן ![g:[c,d]\to\mathbb R](/images/math/4/7/e/47e54f5c5ac4f2174d7fe3833509cbd4.png) פונקציה רציפה אז
פונקציה רציפה אז 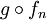 היא סדרת פונקציות המתכנסות במ"ש לפונקצית הגבול
היא סדרת פונקציות המתכנסות במ"ש לפונקצית הגבול 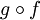 .
.
פתרון
נשים לב כי g רציפה בקטע סגור ולכן רציפה במ"ש. כלומר לכל  יש
יש 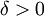 כך שאם
כך שאם 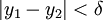 אז
אז 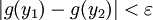 . בנוסף נתון ש-
. בנוסף נתון ש- מתכנסת במ"ש ולכן יש N כך שלכל
מתכנסת במ"ש ולכן יש N כך שלכל 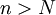 מתקיים
מתקיים 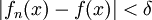 (בפרט אפשר לבחור
(בפרט אפשר לבחור 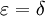 ).
נשים לב ש-
).
נשים לב ש-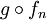 מוגדרת היטב לכל
מוגדרת היטב לכל 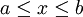 ועבור
ועבור 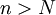 מתקיים
מתקיים 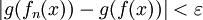 . מכאן ש-
. מכאן ש-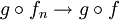 במ"ש.
במ"ש. 
מבחן ה-M של ווירשטראס
יהי 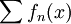 טור פונקציות בקטע I. אם קיים טור מתכנס של מספרים חיוביים
טור פונקציות בקטע I. אם קיים טור מתכנס של מספרים חיוביים 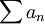 כך שלכל n גדול מספיק ולכל
כך שלכל n גדול מספיק ולכל 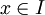 מתקיים
מתקיים 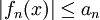 אז
אז 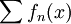 מתכנס במ"ש ב-I.
מתכנס במ"ש ב-I.
דוגמה 4
הוכח כי 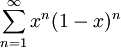 מתכנס במ"ש ב-
מתכנס במ"ש ב-![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
פתרון
נרשום את הטור כ-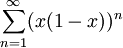 נסמן
נסמן 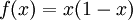 ונחסום אותה:
ונחסום אותה: 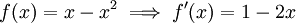 ולכן
ולכן 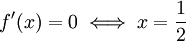 , שהיא מקסימום כי
, שהיא מקסימום כי 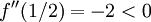 . נותר לבדוק את קצוות הקטע:
. נותר לבדוק את קצוות הקטע: 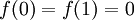 . נסיק ש-
. נסיק ש-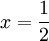 היא נקודת קיצון גלובלית וכן-
היא נקודת קיצון גלובלית וכן-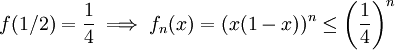 .
. 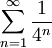 מתכנס (זהו טור הנדסי) ולכן, לפי מבחן ה-M של וירשטרס, הטור
מתכנס (זהו טור הנדסי) ולכן, לפי מבחן ה-M של וירשטרס, הטור 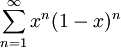 מתכנס במ"ש.
מתכנס במ"ש. 
אינטגרציה איבר-איבר בסדרות
תהי  סדרת פונקציות רציפות המתכנסות במ"ש לפונקציות f בקטע I. אזי f אינטגרבילית בקטע ומתקיים
סדרת פונקציות רציפות המתכנסות במ"ש לפונקציות f בקטע I. אזי f אינטגרבילית בקטע ומתקיים 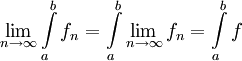 .
.
דוגמה 5
קבע האם 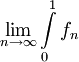 מתכנס כאשר
מתכנס כאשר 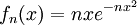 ב-
ב-![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , והאם
, והאם 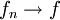 במ"ש.
במ"ש.
פתרון
נציב 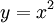 ואז
ואז ![\int\limits_0^1 f_n=\frac n2\int\limits_0^1e^{-ny}\mathrm dy=\frac n2\left[\frac{e^{-ny}}{-n}\right]_{y=0}^1=-\frac12e^{-n}+\frac12\to\frac12](/images/math/c/b/6/cb6da3cb5f1b1d6055385c717fe225aa.png) , כלומר
, כלומר 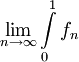 אכן מתכנס. נותר לבדוק אם
אכן מתכנס. נותר לבדוק אם 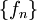 מתכנסת במ"ש:
דרך 1:
מתכנסת במ"ש:
דרך 1: 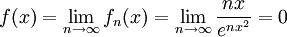 (השיוויון האחרון לפי לופיטל). נניח בשלילה שההתכנסות במ"ש, אבל
(השיוויון האחרון לפי לופיטל). נניח בשלילה שההתכנסות במ"ש, אבל 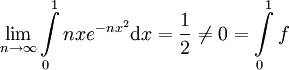 ולכן קיבלנו סתירה. לפיכך ההתכנסות אינה במ"ש.
ולכן קיבלנו סתירה. לפיכך ההתכנסות אינה במ"ש. 
דרך 2: הראנו כבר כי פונקצית הגבול היא 0. נחפש מקסימום ל-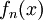 :
: 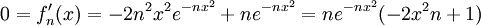 ונקבל
ונקבל 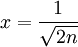 . לכן
. לכן 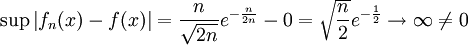 ומכאן שההתכנסות אינה במ"ש.
ומכאן שההתכנסות אינה במ"ש. 