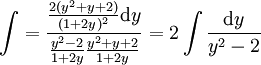משתמש:אור שחף/133 - תרגול/27.3.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - תרגול
גרסה מ־17:01, 27 במרץ 2011 מאת אור שחף (שיחה | תרומות) (יצירת דף עם התוכן "=אינטגרציה {{הערה|(המשך)}}= עד כה דיברנו על אינטגרלים של פונקציות רציונליות (בפרט פולינומים), ...")
תוכן עניינים
אינטגרציה (המשך)
עד כה דיברנו על אינטגרלים של פונקציות רציונליות (בפרט פולינומים), פונקציות טריגונומטריות וכו'.
עתה נדבר על פונקציות לא רציונליות.
דוגמה 1
חשב
-
![\int\frac{\mathrm dx}{x\left(\sqrt x+\sqrt[5]{x^2}\right)}](/images/math/2/1/b/21bab81c3d7cdfcb273267192541db00.png) . ====פתרון==== נרשום את האינטגרל כ-
. ====פתרון==== נרשום את האינטגרל כ-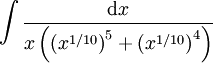 . מתבקשת ההצבה
. מתבקשת ההצבה 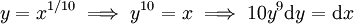 ולכן נקבל
ולכן נקבל 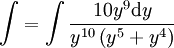 ומכאן קל למצוא את הפתרון.
ומכאן קל למצוא את הפתרון. -
![\int\frac{x^2+\sqrt{1+x}}\sqrt[3]{1+x}\mathrm dx](/images/math/e/e/8/ee89f5e5b475d63d79100f0445446117.png) ====פתרון==== נגדיר
====פתרון==== נגדיר 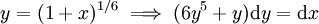 . נקבל
. נקבל 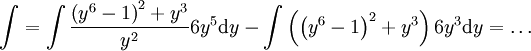
הצבות טריגונומטריות
כאשר יש פונקציה מהצורה 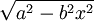 .
.
דוגמה 2
-
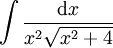 ====פתרון==== נעזר במשלש ישר זווית: גרף (1)
====פתרון==== נעזר במשלש ישר זווית: גרף (1) 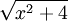 חייב להיות אורך היתר. ההצבה המתבקשת היא
חייב להיות אורך היתר. ההצבה המתבקשת היא 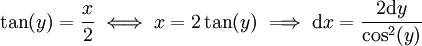 . נקבל
. נקבל 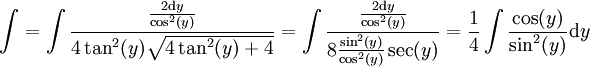 . נציב
. נציב 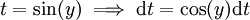 אזי
אזי 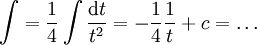
-
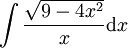 ====פתרון==== שוב נבנה משולש גרף 2. מתבקשת ההצבה
====פתרון==== שוב נבנה משולש גרף 2. מתבקשת ההצבה 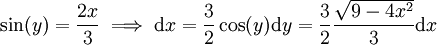 אזי
אזי 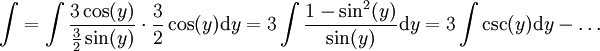 . נותר לפתור
. נותר לפתור 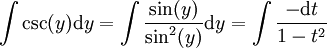 עבור
עבור 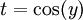 . מכאן נותר רק לפתור בשברים חלקיים.
. מכאן נותר רק לפתור בשברים חלקיים. - עיבוד הנוסחה נכשל (שגיאת תחביר): \int\frac{\mathrm dx}{\left(4(x-3)^2-9\right)^\frac32
====פתרון==== ראשית נציב עיבוד הנוסחה נכשל (שגיאת תחביר): y=x-y\implies \int=\int\frac{\mathrm dy}{\left(y^3-9\right)^\frac32
. נציב 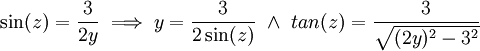 נקבל:
נקבל: 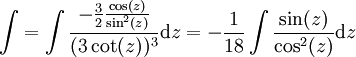 את האינטגרל הנ"ל קל לפתור ע"י הצבה
את האינטגרל הנ"ל קל לפתור ע"י הצבה 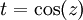 ואז
ואז 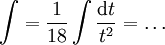
הצבות מיוחדות
ההצבה האוניברסלית: תמיד ניתן להציב 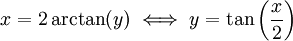 ולכן
ולכן 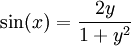 וגם
וגם 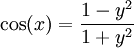 .
.
דוגמה 3
פתור את האינטגרלים הבאים באמצעות ההצבה האוניברסלית:
-
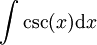 ====פתרון====
====פתרון==== 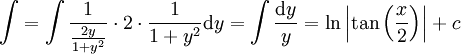
-
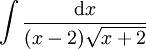 =====פתרון==== נציב
=====פתרון==== נציב 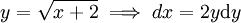 לפיכך
לפיכך 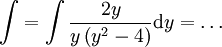 . מסכנה: כאשר יש ביטוי מהצורה
. מסכנה: כאשר יש ביטוי מהצורה ![\sqrt[n]{ax+b}](/images/math/8/1/6/81609a67530c44caab097cbce3373a1d.png) ננסה להציב
ננסה להציב 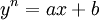 .
.
אם יש ביטוי מהצורה 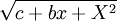 כאשר הפולינום אי פריק נציב
כאשר הפולינום אי פריק נציב 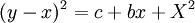 . אם הפולינום בשורש כן פריק ושורשיו
. אם הפולינום בשורש כן פריק ושורשיו 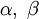 נציב עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): c+bx+X^2=(\beta-x)^2^2
נציב עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): c+bx+X^2=(\beta-x)^2^2
או עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): c+bx+X^2=(\alpha-x)^2^2
דוגמה 4
נחשב 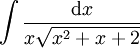 ====פתרון==== הפולינום שבשורש אי פריק, לכן נגדיר y עבורו
====פתרון==== הפולינום שבשורש אי פריק, לכן נגדיר y עבורו 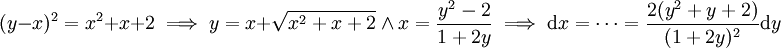 ואז
ואז