משתמש:אור שחף/133 - תרגול/29.5.11
תוכן עניינים
סכומי טורים
תזכורת: (אינטגרציה איבר איבר בסדרות) אם  סדרת פונקציות רציפות המתכנסות במ"ש לפונקציה f ב-
סדרת פונקציות רציפות המתכנסות במ"ש לפונקציה f ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , אז f אינטגרבילית ומתקיים
, אז f אינטגרבילית ומתקיים 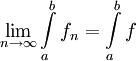 . באופן דומה ננסח עבור גזירה איבר-איבר בסדרות:
. באופן דומה ננסח עבור גזירה איבר-איבר בסדרות:  סדרת פונקציות גזירות ורציפות ב-
סדרת פונקציות גזירות ורציפות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) המתכנסת בנקודה אחת
המתכנסת בנקודה אחת ![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) ל-
ל-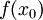 . אם
. אם 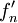 סדרת פונקציות המתכנסות במ"ש ב-
סדרת פונקציות המתכנסות במ"ש ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז  גזירה
גזירה 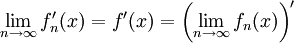 . באופן דומה נגדיר עבור טורים. עבור אינטגרציה לדוגמה: יהי
. באופן דומה נגדיר עבור טורים. עבור אינטגרציה לדוגמה: יהי 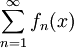 טור של פונקציות רציפות ב-
טור של פונקציות רציפות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) המתכנס במ"ש בקטע לפונקצית סכום
המתכנס במ"ש בקטע לפונקצית סכום 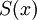 אז טור המספרים מתכנס ומתקיים
אז טור המספרים מתכנס ומתקיים 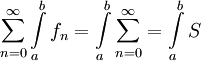 .
.
דוגמה 1
- הוכח שלכל
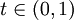 מתקיים
מתקיים 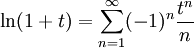 .
. - חשב
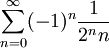 . פתרון: נעזר בתרגיל בטור הנדסי, ידוע ש-
. פתרון: נעזר בתרגיל בטור הנדסי, ידוע ש-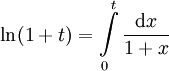 . בנוסף ידוע שמתקיים
. בנוסף ידוע שמתקיים 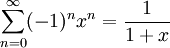 (לפי סדרה הנדסית). מספיק להראות שהטור הנ"ל במ"ש בקטע סגור מהצורה
(לפי סדרה הנדסית). מספיק להראות שהטור הנ"ל במ"ש בקטע סגור מהצורה ![[-a,a]](/images/math/1/8/8/188b8d2ccb3b1d52985a3a3e5cf71fdb.png) . נשתמש במבחן ה-M של וירשטרס
. נשתמש במבחן ה-M של וירשטרס 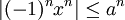 (עבור הקטע הסגור הנ"ל
(עבור הקטע הסגור הנ"ל ![[-a,a]](/images/math/1/8/8/188b8d2ccb3b1d52985a3a3e5cf71fdb.png) ) אם
) אם 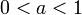 ברור ש-
ברור ש-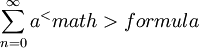 </math> מתכנס ולכן לפי מבחן ה-M הטור המקורי מתכנס במ"ש.
</math> מתכנס ולכן לפי מבחן ה-M הטור המקורי מתכנס במ"ש.
יהי 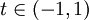 , נסתכל על הקטע מהצורה
, נסתכל על הקטע מהצורה ![[0,t]](/images/math/2/1/b/21b8fce671acf5fa4690193ad7ef3461.png) שם
שם 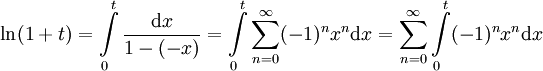 (הראנו שהטור מתכנס במ"ש לפי וירשטרס, נחליף בין האינטגרציה לסכימה). זה שווה ל-
(הראנו שהטור מתכנס במ"ש לפי וירשטרס, נחליף בין האינטגרציה לסכימה). זה שווה ל-![\left[\sum_{n=0}^\infty(-1)^n\frac{x^{n+1}}{n+1}\right]_{x=0}^1=\sum_{n=0}^\infty \frac{(-1)^nt^{n+1}}{n+1}=\sum_{n=1}^\infty\frac{(-1)^{n+1}t^n}n](/images/math/f/e/2/fe2a0d54001c52ad54299694a0a8181d.png)
ב. ברור כי 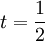 נמצא בקטע, שם יש התכנסות (כי תחום ההתכנסות טור הנדסי)
נמצא בקטע, שם יש התכנסות (כי תחום ההתכנסות טור הנדסי) 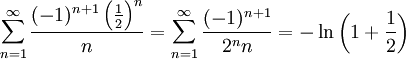
גזירה איבר איבר של טורי פונקציות: יהיו  פונציות גזירות רציפות ב-
פונציות גזירות רציפות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך שהטור
כך שהטור  מתכנס ב-
מתכנס ב-![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) ל-
ל-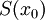 אם טור הנגזרות
אם טור הנגזרות 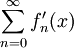 מתכנס במידה שווה בקטע אז מתקיים
מתכנס במידה שווה בקטע אז מתקיים 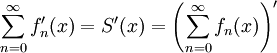 .
.
דוגמה 2
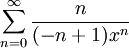 . חשבו את סכום הטור עבור
. חשבו את סכום הטור עבור 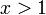 .
.
פתרון
נתייחס לטור הבא 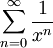 שידוע שמתכנס עבור
שידוע שמתכנס עבור 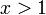 .
.
יש להראות כי הטור מתכנס במ"ש. ברור שע"י הצבה 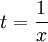 באופן דומה לתרגיל נקבל התכנסות במ"ש.
באופן דומה לתרגיל נקבל התכנסות במ"ש.
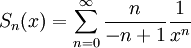 .
.
הראנו בשאלת הכנה כי הטור מתכנס במ"ש, נשאר לעשות אינטגרציה 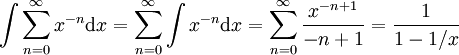 . עד כאן
. עד כאן 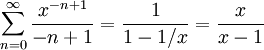 . צריך להגיע לטור המבוקש. ברור כי
. צריך להגיע לטור המבוקש. ברור כי 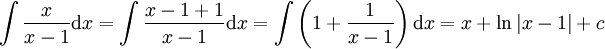 . נשאר לחלק ב-x ואז לגזור.
. נשאר לחלק ב-x ואז לגזור.
דוגמה 2.5 (המטרה להסביר את דוגמה 2)
מהו סכום הטור 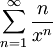 עבור
עבור 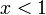 .
.
פתרון
נשים לב שאם נגדיר 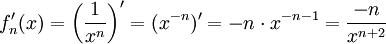 ז"א
ז"א 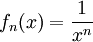 . אם
. אם 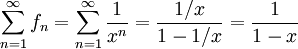 . נבדוק את התנאים למשפט "גזירה איבר-איבר של טור פונקציות". דרוש ש-
. נבדוק את התנאים למשפט "גזירה איבר-איבר של טור פונקציות". דרוש ש-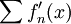 יתכנס במ"ש.
יתכנס במ"ש.
נעזר במבחן ה-M של וירשטרס. אם 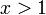 אז יש
אז יש 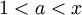 שם מתקיים עיבוד הנוסחה נכשל (שגיאת תחביר): \left|\frac{-n}{x^{n+1}}\right|\le\left|\frac n{a^{n+1}}
. הטור
שם מתקיים עיבוד הנוסחה נכשל (שגיאת תחביר): \left|\frac{-n}{x^{n+1}}\right|\le\left|\frac n{a^{n+1}}
. הטור 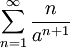 טור מתכנס עפ"י מבחן דלאמר או מבחן השורש).
טור מתכנס עפ"י מבחן דלאמר או מבחן השורש).
נסיק לפי מבחן ה-M של וירשטרס שהטור 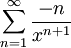 מתכנס במ"ש ולכן אפשר להחליף סדר גזירה.
מתכנס במ"ש ולכן אפשר להחליף סדר גזירה. 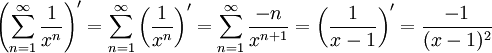 לסיכום
לסיכום 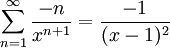 .
.
טור חזקות
רדיוס ההתכנסות של טור חזקות 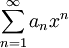 הוא
הוא ![\frac1{\limsup_{n\to\infty}\sqrt[n]{|a_n|}}](/images/math/1/d/b/1dbfb81a91c0c11bf9f2538080189421.png) ןקצוות הטור נבדוק בנפרד.
ןקצוות הטור נבדוק בנפרד.
דוגמה 3
מצא תחום התכנסות של הטור ![\sum_{n=1}^\infty\frac{x^n}\sqrt[3]n](/images/math/0/0/7/00747b6a93f81bbd01d80dda37a6d9d4.png)
פתרון
אכן מדובר על חזקות כי ![\sum=\sum_{n=1}^\infty \frac1\sqrt[3]nx^n](/images/math/0/0/9/009c98f6ba0c93c18358715e1515be76.png) ולכן
ולכן ![a_n=\frac1\sqrt[3]n](/images/math/7/7/1/771016d00f8faecaca4a1ffb64761bb9.png) ואז רדיוס ההתכנסות הוא
ואז רדיוס ההתכנסות הוא ![R=\frac1{\limsup_{n\to\infty}\sqrt[n]\frac1\sqrt[3]n}=1](/images/math/f/c/2/fc2bc1e38a30433ba3ba3ee00788d842.png) . ז"א
. ז"א 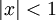 נשאר לבדוק האם יש התכנסות בקצוות
נשאר לבדוק האם יש התכנסות בקצוות 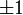 . עבור
. עבור 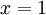 :
: ![\sum_{n=1}^\infty \frac{1^n}\sqrt[3]n](/images/math/d/2/3/d23bec4b81c53df7fc40520549ae1fce.png) שמתבדר כי
שמתבדר כי 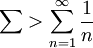 ולכן לפי מבחן ההשוואה מתבדר.
ולכן לפי מבחן ההשוואה מתבדר.
עבור 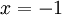 : ברור שהטור מתכנס לפי טור לייבניץ. לסיכום תחום ההתכנסות הוא
: ברור שהטור מתכנס לפי טור לייבניץ. לסיכום תחום ההתכנסות הוא 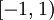 .
.
דוגמה 4
חשבו את תחום ההתכנסות של 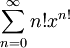 . נשים לב כי הטור הנתון לא טור חזקות. "נתקן" את הטור לטור חזקות. נסתכל קודם על המקור. נסמן
. נשים לב כי הטור הנתון לא טור חזקות. "נתקן" את הטור לטור חזקות. נסתכל קודם על המקור. נסמן 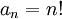 ונגדיר
ונגדיר 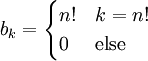 . ברגע זה נקבל את הטור
. ברגע זה נקבל את הטור 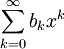 .נשים לב שאכן במקרה הזה נצטרך את ה-
.נשים לב שאכן במקרה הזה נצטרך את ה-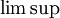 .
.![\limsup_{n\to\infty}\frac1\sqrt[n]{b_k}=\lim_{n\to\infty}\sqrt[n]n=1](/images/math/d/3/8/d383348839a4913473cc4de197ba33e7.png) ולכן רדיוס ההתכנסות הוא 1. נבדוק בקצוות: ב-1 הטור הוא
ולכן רדיוס ההתכנסות הוא 1. נבדוק בקצוות: ב-1 הטור הוא 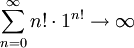 . ועבור
. ועבור 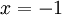 הטור הוא
הטור הוא 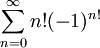 גם אינסוף כי
גם אינסוף כי 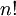 זוגי לכל
זוגי לכל 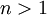 .
.