הבדלים בין גרסאות בדף "ערכים עצמיים ווקטורים עצמיים"
(יצירת דף עם התוכן "'''הערה:''' בסיכום זה, גם אם לא יצויין בכל מקום, <math>V</math> הוא מרחב וקטורי מעל השדה <math>\mathbb{F}</math>...") |
|||
| (13 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | + | חזרה ל[[סיכום הקורס: לינארית 2 (סמסטר א תשעג)]] | |
| + | |||
| + | ''הערה:'' | ||
בסיכום זה, גם אם לא יצויין בכל מקום, <math>V</math> הוא מרחב וקטורי מעל השדה <math>\mathbb{F}</math>, וכן <math>dim V=n</math>. | בסיכום זה, גם אם לא יצויין בכל מקום, <math>V</math> הוא מרחב וקטורי מעל השדה <math>\mathbb{F}</math>, וכן <math>dim V=n</math>. | ||
| + | בנוסף, <math>A\in M_n (\mathbb{F})</math>. | ||
| שורה 11: | שורה 14: | ||
'''הגדרה:''' | '''הגדרה:''' | ||
| − | תהי <math>A\in M_n (\mathbb{F})</math>. אומרים ש-<math>\lambda\in\mathbb{F}</math> הוא ערך עצמי של <math>A</math> אם קיים וקטור <math>0\neq v\in\mathbb{F}^n</math> שעבורו <math>Av=\lambda v</math>. הוקטור <math>v</math> נקרא וקטור עצמי של <math>A</math> הקשור ל-<math>\lambda</math>. | + | תהי <math>A\in M_n (\mathbb{F})</math>. אומרים ש-<math>\lambda\in\mathbb{F}</math> הוא ערך עצמי (ע"ע) של <math>A</math> אם קיים וקטור <math>0\neq v\in\mathbb{F}^n</math> שעבורו <math>Av=\lambda v</math>. הוקטור <math>v</math> נקרא וקטור עצמי (ו"ע) של <math>A</math> הקשור ל-<math>\lambda</math>. |
'''הגדרה:''' | '''הגדרה:''' | ||
| − | אוסף כל | + | אוסף כל הע"ע של <math>A</math> נקרא הספקטרום של <math>A</math>, ומסומן <math>spec(A)</math>. |
| + | |||
| + | ''הערה:'' | ||
| + | יכול להיות המצב <math>spec(A)=\varnothing</math>. | ||
| + | |||
| + | |||
| + | '''משפט:''' | ||
| + | |||
| + | <math>\lambda=0</math> הוא ע"ע של <math>A</math> אם ורק אם <math>A</math> אינה הפיכה. | ||
| + | |||
| + | ''הערה:'' | ||
| + | <math>A</math> אינה הפיכה אם ורק אם <math>det(A)=0</math>. | ||
| + | |||
| + | |||
| + | '''משפט:''' | ||
| + | |||
| + | <math>\lambda\in\mathbb{F}</math> הוא ע"ע של מטריצה <math>A\in M_n (\mathbb{F})</math> אם ורק אם <math>det(\lambda I-A)=0</math>. | ||
| + | |||
| + | |||
| + | '''דוגמה למציאת ע"ע:''' | ||
| + | |||
| + | '' <math>A=I_n</math>.'' | ||
| + | |||
| + | שיטה ראשונה: <math>I_n v=\lambda v</math> <math>\Leftarrow</math> <math>v=\lambda v</math> <math>\Leftarrow</math> <math>\lambda=1</math> <math>\Leftarrow</math> <math>spec(A)=\left \{1 \right \}</math>. | ||
| + | |||
| + | שיטה שנייה: לפי המשפט. | ||
| + | <math>\lambda I_n-I_n=\begin{pmatrix} | ||
| + | \lambda-1 & &0 \\ | ||
| + | & \ddots & \\ | ||
| + | 0 & & \lambda-1 | ||
| + | \end{pmatrix}</math>, כלומר <math>det(\lambda I_n-I_n)=(\lambda-1)^n</math>, ומכאן <math>(\lambda-1)^n=0</math> <math>\Leftrightarrow</math> <math>\lambda=1</math>. | ||
| + | |||
| + | |||
| + | '''הגדרה:''' | ||
| + | |||
| + | יהי <math>T:V\rightarrow V</math> אופרטור לינארי. אומרים ש-<math>\lambda\in\mathbb{F}</math> הוא ע"ע של <math>T</math> אם קיים וקטור <math>0\neq v\in\mathbb{F}^n</math> שעבורו <math>Tv=T(v)=\lambda v</math>. הוקטור <math>v</math> נקרא ו"ע של <math>T</math> הקשור ל-<math>\lambda</math>. | ||
| + | |||
| + | |||
| + | '''משפט:''' | ||
| + | |||
| + | יהי <math>T:V\rightarrow V</math> אופרטור לינארי, יהי <math>B</math> בסיס של <math>V</math> ותהי <math>A=[T]_B</math> המטריצה המייצגת של <math>T</math> יחסית לבסיס <math>B</math>. אזי אם <math>\lambda\in\mathbb{F}</math> הוא ע"ע של <math>T</math>, אז <math>\lambda</math> הוא גם ע"ע של <math>A</math>. | ||
| + | |||
| + | |||
| + | '''אלגוריתם לחיפוש ע"ע של אופרטור לינארי <math>T:V\rightarrow V</math>:''' | ||
| + | |||
| + | 1. נבחר בסיס <math>B</math> של <math>V</math>. | ||
| + | |||
| + | 2. נחשב את המטריצה המייצגת <math>A</math>. | ||
| + | |||
| + | 3. נרכיב את המשוואה <math>det(\lambda I-A)=0</math>. זוהי משוואה ממעלה <math>n</math> עם משתנה יחיד <math>\lambda</math>. | ||
| + | |||
| + | 4. נחפש פתרונות <math>\lambda_1,...,\lambda_s</math>, שהם הע"ע של <math>T</math>. | ||
גרסה אחרונה מ־10:39, 5 בינואר 2013
חזרה לסיכום הקורס: לינארית 2 (סמסטר א תשעג)
הערה:
בסיכום זה, גם אם לא יצויין בכל מקום,  הוא מרחב וקטורי מעל השדה
הוא מרחב וקטורי מעל השדה  , וכן
, וכן 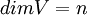 .
בנוסף,
.
בנוסף, 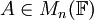 .
.
הגדרה:
העתקה לינארית 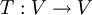 (ממרחב לעצמו) תיקרא אופרטור לינארי.
(ממרחב לעצמו) תיקרא אופרטור לינארי.
הגדרה:
תהי 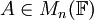 . אומרים ש-
. אומרים ש-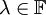 הוא ערך עצמי (ע"ע) של
הוא ערך עצמי (ע"ע) של  אם קיים וקטור
אם קיים וקטור 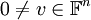 שעבורו
שעבורו 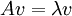 . הוקטור
. הוקטור 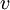 נקרא וקטור עצמי (ו"ע) של
נקרא וקטור עצמי (ו"ע) של  הקשור ל-
הקשור ל- .
.
הגדרה:
אוסף כל הע"ע של  נקרא הספקטרום של
נקרא הספקטרום של  , ומסומן
, ומסומן 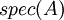 .
.
הערה:
יכול להיות המצב 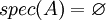 .
.
משפט:
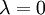 הוא ע"ע של
הוא ע"ע של  אם ורק אם
אם ורק אם  אינה הפיכה.
אינה הפיכה.
הערה:
 אינה הפיכה אם ורק אם
אינה הפיכה אם ורק אם 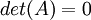 .
.
משפט:
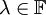 הוא ע"ע של מטריצה
הוא ע"ע של מטריצה 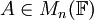 אם ורק אם
אם ורק אם 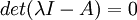 .
.
דוגמה למציאת ע"ע:
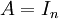 .
.
שיטה ראשונה: 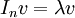
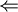
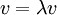
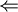
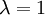
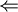
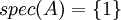 .
.
שיטה שנייה: לפי המשפט.
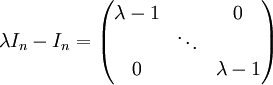 , כלומר
, כלומר 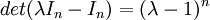 , ומכאן
, ומכאן 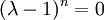
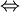
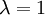 .
.
הגדרה:
יהי 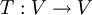 אופרטור לינארי. אומרים ש-
אופרטור לינארי. אומרים ש-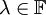 הוא ע"ע של
הוא ע"ע של  אם קיים וקטור
אם קיים וקטור 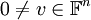 שעבורו
שעבורו 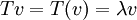 . הוקטור
. הוקטור 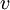 נקרא ו"ע של
נקרא ו"ע של  הקשור ל-
הקשור ל- .
.
משפט:
יהי 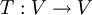 אופרטור לינארי, יהי
אופרטור לינארי, יהי  בסיס של
בסיס של  ותהי
ותהי ![A=[T]_B](/images/math/4/4/f/44f2307ba089fab340788991481d6621.png) המטריצה המייצגת של
המטריצה המייצגת של  יחסית לבסיס
יחסית לבסיס  . אזי אם
. אזי אם 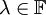 הוא ע"ע של
הוא ע"ע של  , אז
, אז  הוא גם ע"ע של
הוא גם ע"ע של  .
.
אלגוריתם לחיפוש ע"ע של אופרטור לינארי 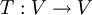 :
:
1. נבחר בסיס  של
של  .
.
2. נחשב את המטריצה המייצגת  .
.
3. נרכיב את המשוואה 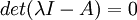 . זוהי משוואה ממעלה
. זוהי משוואה ממעלה  עם משתנה יחיד
עם משתנה יחיד  .
.
4. נחפש פתרונות 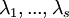 , שהם הע"ע של
, שהם הע"ע של  .
.