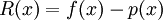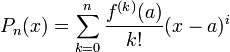הבדלים בין גרסאות בדף "פולינום טיילור"
מתוך Math-Wiki
(←פולינום טיילור) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 1: | שורה 1: | ||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
| − | + | כיון שכפל וחיבור הן פעולות שקל לחשבן, פולינומים הן פונקציות שקל לחשבן את ערכן בכל נקודה. לכן, בהנתן פונקציה כללית <math>f</math> , היינו שמחים למצוא פולינום קרוב אליה. כלומר, היינו רוצים למצוא פולינום <math>p</math> כך שהשארית | |
| − | + | :<math>R(x)=f(x)-p(x)</math> | |
| − | + | תהא "מינימלית". שימו לב כי הגדרת המינימליות תלויה בצורך. לדוגמא, יתכן ונרצה כי השארית תהא חסומה על כל הממשיים או תשאף לאפס בנקודה מסויימת. | |
| − | + | ||
| − | תהא "מינימלית". שימו לב כי הגדרת | + | |
==פולינום טיילור== | ==פולינום טיילור== | ||
| − | + | '''פולינום טיילור סביב נקודה <math>a</math>''' מדרגה <math>n</math> הנו פולינום מהצורה: | |
| − | '''פולינום טיילור סביב נקודה a''' מדרגה n | + | :<math>P_n(x)=\sum_{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a)^i</math> |
| − | + | כאשר <math>f^{(n)}</math> היא הנגזרת ה- <math>n</math> של <math>f</math> . | |
| − | + | ||
| − | + | ||
| − | כאשר <math>f^{(n)}</math> היא הנגזרת ה-n של f | + | |
| − | שימו לב שבאופן ברור מההגדרה קיום פולינום טיילור מדרגה n דורש שהפונקציה תהא גזירה לפחות n פעמים בנקודה a. אנחנו נראה מיד שעל מנת להעריך את השגיאה של הפולינום נדרוש כי הפונקציה תהא גזירה '''לפחות n+1''' פעמים ''' | + | שימו לב שבאופן ברור מההגדרה קיום פולינום טיילור מדרגה <math>n</math> דורש שהפונקציה תהא גזירה לפחות <math>n</math> פעמים בנקודה <math>a</math> . אנחנו נראה מיד שעל-מנת להעריך את השגיאה של הפולינום נדרוש כי הפונקציה תהא גזירה '''לפחות <math>n+1</math>''' פעמים '''באזור''' הנקודה <math>a</math> . |
פולינום טיילור משמש לקירוב פונקציות מסיבות שנראה בהמשך ([[טור חזקות]]), ובזכות [[משפט טיילור עם שארית לגראנז']] | פולינום טיילור משמש לקירוב פונקציות מסיבות שנראה בהמשך ([[טור חזקות]]), ובזכות [[משפט טיילור עם שארית לגראנז']] | ||
גרסה מ־11:55, 7 ביוני 2016
כיון שכפל וחיבור הן פעולות שקל לחשבן, פולינומים הן פונקציות שקל לחשבן את ערכן בכל נקודה. לכן, בהנתן פונקציה כללית 
, היינו שמחים למצוא פולינום קרוב אליה. כלומר, היינו רוצים למצוא פולינום 
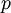כך שהשארית
תהא "מינימלית". שימו לב כי הגדרת המינימליות תלויה בצורך. לדוגמא, יתכן ונרצה כי השארית תהא חסומה על כל הממשיים או תשאף לאפס בנקודה מסויימת.
פולינום טיילור
פולינום טיילור סביב נקודה 
מדרגה 
הנו פולינום מהצורה:
כאשר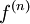 
היא הנגזרת ה- של .
שימו לב שבאופן ברור מההגדרה קיום פולינום טיילור מדרגה דורש שהפונקציה תהא גזירה לפחות פעמים בנקודה . אנחנו נראה מיד שעל-מנת להעריך את השגיאה של הפולינום נדרוש כי הפונקציה תהא גזירה לפחות 
פעמים באזור הנקודה .
פולינום טיילור משמש לקירוב פונקציות מסיבות שנראה בהמשך (טור חזקות), ובזכות משפט טיילור עם שארית לגראנז'
