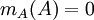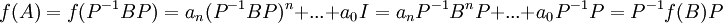הבדלים בין גרסאות בדף "פולינום מינימלי"
מתוך Math-Wiki
(יצירת דף עם התוכן "==הגדרה== תהי A מטריצה ריבועית. אזי הפולינום המינימלי של A, מסומן <math>m_A(x)</math> הוא הפולינום המת...") |
|||
| שורה 11: | שורה 11: | ||
*לפולינום האופייני והפולינום המינימלי בדיוק אותם גורמים אי פריקים. בפרט, השורשים של הפולינום המינימלי הם הערכים העצמיים של המטריצה. | *לפולינום האופייני והפולינום המינימלי בדיוק אותם גורמים אי פריקים. בפרט, השורשים של הפולינום המינימלי הם הערכים העצמיים של המטריצה. | ||
| + | |||
| + | ==תרגילים== | ||
| + | |||
| + | ===א=== | ||
| + | הוכח כי למטריצות דומות אותו פולינום מינימלי | ||
| + | |||
| + | |||
| + | '''הוכחה.''' | ||
| + | |||
| + | ראשית נשים לב לעובדה הבאה- יהי פולינום f ותהיינה מטריצות דומות A,B אזי גם המטריצות <math>f(A),f(B)</math> דומות. | ||
| + | |||
| + | אכן, נסמן <math>f(x)=a_nx^n+...+a_0</math> ונסמן <math>A=P^{-1}BP</math>. לכן: | ||
| + | |||
| + | |||
| + | מסקנה: נניח A,B מטריצות דומות, אזי לכל פולינום f מתקיים <math>f(A)=0</math> אם"ם <math>f(B)=0</math>. | ||
| + | |||
| + | אכן, המטריצה היחידה הדומה למטריצת האפס הינה מטריצת האפס עצמה. כיוון ש<math>f(A),f(B)</math> דומות, המסקנה נובעת. | ||
| + | |||
| + | |||
| + | בסה"כ, כיוון שהפולינומים המאפסים מטריצות דומות הם אותם פולינומים, בפרט המינימלי המתוקן מבינהם הוא אותו אחד. | ||
| + | |||
| + | ===ב=== | ||
| + | ::<math>f(A)=f(P^{-1}BP)=a_n(P^{-1}BP)^n+...+a_0I = a_nP^{-1}B^nP+...+a_0P^{-1}P = P^{-1}f(B)P</math> | ||
| + | |||
| + | |||
| + | |||
| + | [[קטגוריה:אלגברה לינארית]] | ||
גרסה מ־07:02, 13 בנובמבר 2012
הגדרה
תהי A מטריצה ריבועית. אזי הפולינום המינימלי של A, מסומן 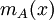 הוא הפולינום המתוקן מהדרגה הנמוכה ביותר המקיים
הוא הפולינום המתוקן מהדרגה הנמוכה ביותר המקיים
הערה: פולינום מתוקן הינו פולינום מהצורה 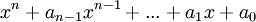 , כלומר המקדם של המונום בעל החזקה הגבוהה ביותר הינו אחד.
, כלומר המקדם של המונום בעל החזקה הגבוהה ביותר הינו אחד.
תכונות
- לכל פולינום f כך ש
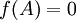 מתקיים
מתקיים 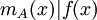 . בפרט ממשפט קיילי-המילטון נובע כי הפולינום המינימלי מחלק את הפולינום האופייני
. בפרט ממשפט קיילי-המילטון נובע כי הפולינום המינימלי מחלק את הפולינום האופייני
- לפולינום האופייני והפולינום המינימלי בדיוק אותם גורמים אי פריקים. בפרט, השורשים של הפולינום המינימלי הם הערכים העצמיים של המטריצה.
תרגילים
א
הוכח כי למטריצות דומות אותו פולינום מינימלי
הוכחה.
ראשית נשים לב לעובדה הבאה- יהי פולינום f ותהיינה מטריצות דומות A,B אזי גם המטריצות 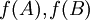 דומות.
דומות.
אכן, נסמן 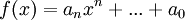 ונסמן
ונסמן 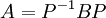 . לכן:
. לכן:
מסקנה: נניח A,B מטריצות דומות, אזי לכל פולינום f מתקיים 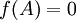 אם"ם
אם"ם 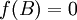 .
.
אכן, המטריצה היחידה הדומה למטריצת האפס הינה מטריצת האפס עצמה. כיוון ש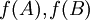 דומות, המסקנה נובעת.
דומות, המסקנה נובעת.
בסה"כ, כיוון שהפולינומים המאפסים מטריצות דומות הם אותם פולינומים, בפרט המינימלי המתוקן מבינהם הוא אותו אחד.