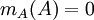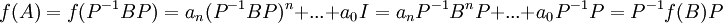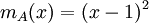הבדלים בין גרסאות בדף "פולינום מינימלי"
(←ב) |
|||
| שורה 38: | שורה 38: | ||
===ב=== | ===ב=== | ||
| + | תהי A ריבועית כך שהפולינום המינמלי שלה הינו | ||
| + | |||
| + | :<math>m_A(x)=(x-1)^2</math> | ||
| + | |||
| + | יהא <math>f(x)=x^2+4x+3</math>, הוכח כי המטריצה <math>f(A)</math> הפיכה. | ||
| + | |||
| + | |||
| + | '''פתרון.''' | ||
| + | |||
| + | <math>f(A)=A^2+4A+3I = (A-I)^2+6A+2I = 6A+2I</math> | ||
| + | |||
| + | |||
| + | כעת, נוכיח כי <math>|f(A)|\neq 0</math> ולכן המטריצה הפיכה. | ||
| + | |||
| + | |||
| + | נניח בשלילה כי <math>|f(A)|= 0</math> לכן <math>|6A+2I|=0</math> ולכן <math>|A-\frac{-2}{6}I|=0</math> | ||
| + | |||
| + | |||
| + | אם כן, <math>\frac{-2}{6}</math> הוא ע"ע של המטריצה A, אבל הוא אינו שורש של הפולינום המינימלי הנתון, בסתירה. | ||
| + | |||
| + | ===ג=== | ||
גרסה מ־07:46, 13 בנובמבר 2012
הגדרה
תהי A מטריצה ריבועית. אזי הפולינום המינימלי של A, מסומן 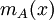 הוא הפולינום המתוקן מהדרגה הנמוכה ביותר המקיים
הוא הפולינום המתוקן מהדרגה הנמוכה ביותר המקיים
הערה: פולינום מתוקן הינו פולינום מהצורה 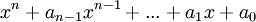 , כלומר המקדם של המונום בעל החזקה הגבוהה ביותר הינו אחד.
, כלומר המקדם של המונום בעל החזקה הגבוהה ביותר הינו אחד.
תכונות
- לכל פולינום f כך ש
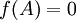 מתקיים
מתקיים 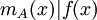 . בפרט ממשפט קיילי-המילטון נובע כי הפולינום המינימלי מחלק את הפולינום האופייני
. בפרט ממשפט קיילי-המילטון נובע כי הפולינום המינימלי מחלק את הפולינום האופייני
- לפולינום האופייני והפולינום המינימלי בדיוק אותם גורמים אי פריקים. בפרט, השורשים של הפולינום המינימלי הם הערכים העצמיים של המטריצה.
- מסקנה: על מנת לחשב את הפולינום האופייני, נמצא את הפולינום המכיל את הגורמים האי פריקים של הפולינום האופייני, בחזקות הכי נמוכות, המאפס את המטריצה
תרגילים
א
הוכח כי למטריצות דומות אותו פולינום מינימלי
הוכחה.
ראשית נשים לב לעובדה הבאה- יהי פולינום f ותהיינה מטריצות דומות A,B אזי גם המטריצות 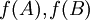 דומות.
דומות.
אכן, נסמן 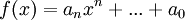 ונסמן
ונסמן 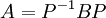 . לכן:
. לכן:
מסקנה: נניח A,B מטריצות דומות, אזי לכל פולינום f מתקיים 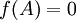 אם"ם
אם"ם 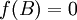 .
.
אכן, המטריצה היחידה הדומה למטריצת האפס הינה מטריצת האפס עצמה. כיוון ש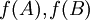 דומות, המסקנה נובעת.
דומות, המסקנה נובעת.
בסה"כ, כיוון שהפולינומים המאפסים מטריצות דומות הם אותם פולינומים, בפרט המינימלי המתוקן מבינהם הוא אותו אחד.
ב
תהי A ריבועית כך שהפולינום המינמלי שלה הינו
יהא 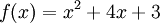 , הוכח כי המטריצה
, הוכח כי המטריצה 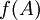 הפיכה.
הפיכה.
פתרון.
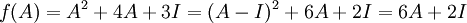
כעת, נוכיח כי 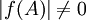 ולכן המטריצה הפיכה.
ולכן המטריצה הפיכה.
נניח בשלילה כי 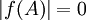 לכן
לכן 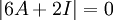 ולכן
ולכן 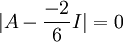
אם כן, 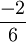 הוא ע"ע של המטריצה A, אבל הוא אינו שורש של הפולינום המינימלי הנתון, בסתירה.
הוא ע"ע של המטריצה A, אבל הוא אינו שורש של הפולינום המינימלי הנתון, בסתירה.