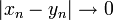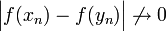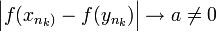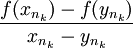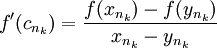הבדלים בין גרסאות בדף "פונקציה רציפה במידה שווה"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) מ |
|||
| שורה 1: | שורה 1: | ||
| − | פונקציה ממשית היא '''רציפה במידה שווה''' בקטע I אם לכל <math> | + | פונקציה ממשית היא '''רציפה במידה שווה''' בקטע I אם לכל <math>\epsilon>0</math> קיים <math>\delta>0</math> כך שלכל <math>x,y</math> בקטע, אם <math>|x-y|<\delta</math> אז <math>\Big|f(x)-f(y)\Big|<\epsilon</math>. תכונה זו גוררת [[פונקציה רציפה|רציפות]] של הפונקציה בכל נקודה, ובדרך כלל היא חזקה יותר. |
| שורה 6: | שורה 6: | ||
===הוכחה=== | ===הוכחה=== | ||
| − | תהי f בעלת נגזרת חסומה בקטע A. נניח בשלילה שהיא אינה רציפה במ"ש לכן קיימות שתי סדרות <math>x_n,y_n</math> בקטע המקיימות | + | תהי <math>f</math> בעלת נגזרת חסומה בקטע <math>A</math> . נניח בשלילה שהיא אינה רציפה במ"ש לכן קיימות שתי סדרות <math>x_n,y_n</math> בקטע המקיימות |
| − | + | :<math>|x_n-y_n|\to 0</math> | |
| − | + | :<math>\Big|f(x_n)-f(y_n)\Big|\not\to 0</math> | |
| − | לכן קיימת תת סדרה כך ש | + | לכן קיימת תת-סדרה כך ש- |
| − | + | :<math>\Big|f(x_{n_k)}-f(y_{n_k})\Big|\to a\ne 0</math> | |
| − | (זוהי תת הסדרה המתכנסת לגבול העליון. אם הגבול העליון היה שווה | + | (זוהי תת-הסדרה המתכנסת לגבול העליון. אם הגבול העליון היה שווה <math>0</math> סדרת הערכים המוחלטים הייתה מתכנסת). |
נובע מכאן כי הסדרה | נובע מכאן כי הסדרה | ||
| − | + | :<math>\frac{f(x_{n_k})-f(y_{n_k})}{x_{n_k}-y_{n_k}}</math> | |
אינה חסומה. | אינה חסומה. | ||
| − | אבל לפי משפט לגראנז, קיימות נקודות <math>c_{n_k}</math> בין <math>x_{n_k},y_{n_k}</math> כך ש | + | אבל לפי משפט לגראנז', קיימות נקודות <math>c_{n_k}</math> בין <math>x_{n_k},y_{n_k}</math> כך ש- |
| − | + | :<math>f'(c_{n_k})=\frac{f(x_{n_k})-f(y_{n_k})}{x_{n_k}-y_{n_k}}</math> | |
ולכן הנגזרת אינה חסומה, בסתירה. | ולכן הנגזרת אינה חסומה, בסתירה. | ||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
גרסה מ־10:14, 8 בפברואר 2016
פונקציה ממשית היא רציפה במידה שווה בקטע I אם לכל 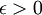 קיים
קיים 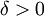 כך שלכל
כך שלכל 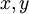 בקטע, אם
בקטע, אם 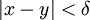 אז
אז 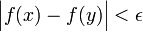 . תכונה זו גוררת רציפות של הפונקציה בכל נקודה, ובדרך כלל היא חזקה יותר.
. תכונה זו גוררת רציפות של הפונקציה בכל נקודה, ובדרך כלל היא חזקה יותר.
משפט
פונקציה בעלת נגזרת חסומה בקטע, רציפה במ"ש באותו קטע
הוכחה
תהי  בעלת נגזרת חסומה בקטע
בעלת נגזרת חסומה בקטע  . נניח בשלילה שהיא אינה רציפה במ"ש לכן קיימות שתי סדרות
. נניח בשלילה שהיא אינה רציפה במ"ש לכן קיימות שתי סדרות 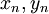 בקטע המקיימות
בקטע המקיימות
לכן קיימת תת-סדרה כך ש-
(זוהי תת-הסדרה המתכנסת לגבול העליון. אם הגבול העליון היה שווה  סדרת הערכים המוחלטים הייתה מתכנסת).
סדרת הערכים המוחלטים הייתה מתכנסת).
נובע מכאן כי הסדרה
אינה חסומה.
אבל לפי משפט לגראנז', קיימות נקודות 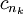 בין
בין 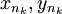 כך ש-
כך ש-
ולכן הנגזרת אינה חסומה, בסתירה.