הבדלים בין גרסאות בדף "פתרון אינפי 1, תש"נ"
מתוך Math-Wiki
| שורה 25: | שורה 25: | ||
==שאלה 3== | ==שאלה 3== | ||
| − | משפט טיילור - תהי <math>f</math> פונקצייה מוגדרת וגזירה <math>n+1</math> פעמים בסביבה <math>S</math> של <math>x_0</math>. אז <math>\forall x \in S: f(x)=P_n(x)+R_n(x)</math>, כאשר <math>P_n(x)=\sum_{k=0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k</math>. | + | א) משפט טיילור - תהי <math>f</math> פונקצייה מוגדרת וגזירה <math>n+1</math> פעמים בסביבה <math>S</math> של <math>x_0</math>. אז <math>\forall x \in S: f(x)=P_n(x)+R_n(x)</math>, כאשר <math>P_n(x)=\sum_{k=0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k</math>. |
| + | ב)תהי <math>f(x)=x^3-4x^2+2x</math>. אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נעשה זאת בכל זאת: | ||
==שאלה 4== | ==שאלה 4== | ||
==שאלה 5== | ==שאלה 5== | ||
גרסה מ־18:09, 4 בפברואר 2012
(המבחן )
שאלה 1
(טענה 7.8 אצל ד"ר שיין:) תהי  פונקצ' המוגדרת בסביבת
פונקצ' המוגדרת בסביבת  . נניח כי
. נניח כי  גזירה ב-
גזירה ב- וגם
וגם 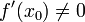 וגם קיימת הפונקצייה ההפוכה
וגם קיימת הפונקצייה ההפוכה 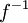 ורציפה בנקודה
ורציפה בנקודה 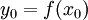 . אזי
. אזי 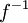 גזירה ב-
גזירה ב-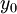 , ונגזרתה שם שווה ל-
, ונגזרתה שם שווה ל- 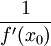 .
.
הוכחה: לפי ההנחה, f גזירה ב- ולכן עפ"י ההגדרה מתקיים
ולכן עפ"י ההגדרה מתקיים 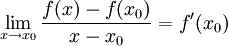 .
.
לפי כללי האריתמטיקה (חשבון) של גבולות, מתקיים: 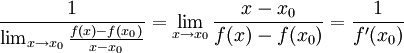 .
.
לפי ההנחות 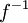 רציפה ב
רציפה ב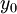 . לכן
. לכן 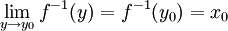 , ובאותו האופן
, ובאותו האופן 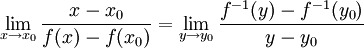 , ולכן בסך הכל קיבלנו ש-
, ולכן בסך הכל קיבלנו ש-
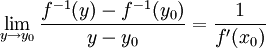 זה נותן את הנדרש עפ"י הגדרת הנגזרת.
זה נותן את הנדרש עפ"י הגדרת הנגזרת.
שאלה 2
נגדיר פונ' 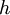 על ידי
על ידי ![\forall x \in [0,2]: h(x)=xf(x)](/images/math/9/e/5/9e532510fcbd6ec9eee7922e0c3be0c6.png) .
h רציפה בקטע הנ"ל כמכפלת 2 פונ' רציפות.
.
h רציפה בקטע הנ"ל כמכפלת 2 פונ' רציפות.
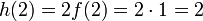 ואילו
ואילו 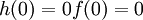 ולכן לפי משפט ערך הביניים
ולכן לפי משפט ערך הביניים ![\exists x_0 \in [0,2]:h(x)=1](/images/math/d/4/6/d46e7a1e6045c35f1d8c07e2050f9339.png) .
.
בנקודה זו מתקיים הדרוש - 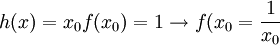 .
.
שאלה 3
א) משפט טיילור - תהי  פונקצייה מוגדרת וגזירה
פונקצייה מוגדרת וגזירה  פעמים בסביבה
פעמים בסביבה 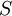 של
של  . אז
. אז 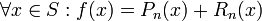 , כאשר
, כאשר 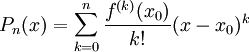 .
.
ב)תהי 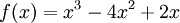 . אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נעשה זאת בכל זאת:
. אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נעשה זאת בכל זאת: