הבדלים בין גרסאות בדף "פתרון אינפי 1, תש"נ"
(←שאלה 5) |
(←שאלה 3) |
||
| שורה 32: | שורה 32: | ||
נחשב נגזרות - <math>f'(x)=(x^3-4x^2+2x)'=3x^2-8x+2</math> | נחשב נגזרות - <math>f'(x)=(x^3-4x^2+2x)'=3x^2-8x+2</math> | ||
| − | <math>f' | + | <math>f''(x)=(3x^2-8x+2)'=6x-8</math> |
| + | <math>f^{(3)}(x)=(6x-8)'=6</math> | ||
| + | <math>f^{(4)}(x)=f^{(5)}(x)=0</math> | ||
| + | |||
| + | <math>P_5(x)=\sum_{k=0}^{5}\frac{f^{(k)}(2)}{k!}(x-2)^k=f(2)+f'(2)(x-2)+f''(2)(x-2)^2+f'''(2)(x-2)^3+0+0</math> | ||
| + | |||
| + | <math>=2^3-4*4+4+(3*4-8*2+2)(x-2)+(12-8)(x-2)^2+6(x-2)^3</math> | ||
| + | |||
| + | <math>P_5(x)=-4-2(x-2)+4(x-2)^2+6(x-2)^3</math>, ועם קצת פתיחת סוגריים ופישוט נקבל את הפולינום שהתחלנו ממנו. מתקיים <math>R_{n+1}(x)=f(x)-P_n(x)</math> ולכן השארית היא 0, כצפוי. | ||
==שאלה 4== | ==שאלה 4== | ||
גרסה מ־19:44, 4 בפברואר 2012
(המבחן )
שאלה 1
(טענה 7.8 אצל ד"ר שיין:) תהי  פונקצ' המוגדרת בסביבת
פונקצ' המוגדרת בסביבת  . נניח כי
. נניח כי  גזירה ב-
גזירה ב- וגם
וגם 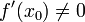 וגם קיימת הפונקצייה ההפוכה
וגם קיימת הפונקצייה ההפוכה 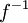 ורציפה בנקודה
ורציפה בנקודה 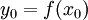 . אזי
. אזי 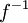 גזירה ב-
גזירה ב-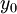 , ונגזרתה שם שווה ל-
, ונגזרתה שם שווה ל- 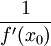 .
.
הוכחה: לפי ההנחה, f גזירה ב- ולכן עפ"י ההגדרה מתקיים
ולכן עפ"י ההגדרה מתקיים 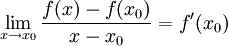 .
.
לפי כללי האריתמטיקה (חשבון) של גבולות, מתקיים: 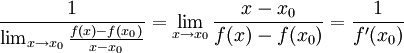 .
.
לפי ההנחות 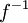 רציפה ב
רציפה ב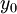 . לכן
. לכן 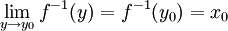 , ובאותו האופן
, ובאותו האופן 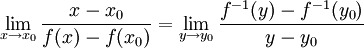 , ולכן בסך הכל קיבלנו ש-
, ולכן בסך הכל קיבלנו ש-
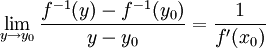 זה נותן את הנדרש עפ"י הגדרת הנגזרת.
זה נותן את הנדרש עפ"י הגדרת הנגזרת.
שאלה 2
נגדיר פונ' 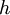 על ידי
על ידי ![\forall x \in [0,2]: h(x)=xf(x)](/images/math/9/e/5/9e532510fcbd6ec9eee7922e0c3be0c6.png) .
h רציפה בקטע הנ"ל כמכפלת 2 פונ' רציפות.
.
h רציפה בקטע הנ"ל כמכפלת 2 פונ' רציפות.
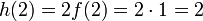 ואילו
ואילו 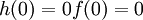 ולכן לפי משפט ערך הביניים
ולכן לפי משפט ערך הביניים ![\exists x_0 \in [0,2]:h(x)=1](/images/math/d/4/6/d46e7a1e6045c35f1d8c07e2050f9339.png) .
.
בנקודה זו מתקיים הדרוש - 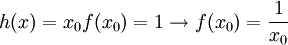 . מש"ל.
. מש"ל.
שאלה 3
א) משפט טיילור - תהי  פונקצייה מוגדרת וגזירה
פונקצייה מוגדרת וגזירה  פעמים בסביבה
פעמים בסביבה 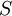 של
של  . אז
. אז 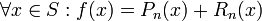 , כאשר
, כאשר 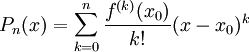 .
.
ב)תהי 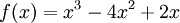 . אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נפתור בכל זאת:
. אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נפתור בכל זאת:
נחשב נגזרות - 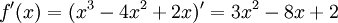
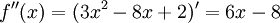
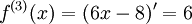
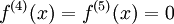
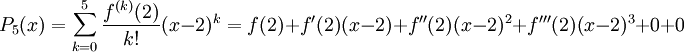
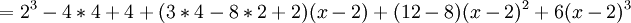
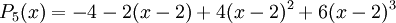 , ועם קצת פתיחת סוגריים ופישוט נקבל את הפולינום שהתחלנו ממנו. מתקיים
, ועם קצת פתיחת סוגריים ופישוט נקבל את הפולינום שהתחלנו ממנו. מתקיים 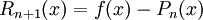 ולכן השארית היא 0, כצפוי.
ולכן השארית היא 0, כצפוי.
שאלה 4
באדיבות וולפראם: קובץ:X+sin2x.pdf
שאלה 5
א) סדרה ממשית 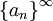 תקרא סדרת קושי אם("ם):
תקרא סדרת קושי אם("ם):
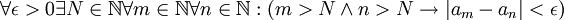
ב)ניקח את הסדרה  שהאיבר ה-
שהאיבר ה- -י בה הוא הקירוב העשרוני עד למקום ה-n של
-י בה הוא הקירוב העשרוני עד למקום ה-n של 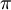 (יותר מגניב משורש 2, אבל פחות נכון כי לך תוכיח שהוא לא רציונלי).
היא של רציונליים, היא מתכנסת מעל הממשיים ולכן היא סדרת קושי, אבל
(יותר מגניב משורש 2, אבל פחות נכון כי לך תוכיח שהוא לא רציונלי).
היא של רציונליים, היא מתכנסת מעל הממשיים ולכן היא סדרת קושי, אבל 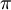 , אם להאמין לספרים, אינו רציונלי.
, אם להאמין לספרים, אינו רציונלי.
שאלה 6
השאלה אמנם לא בחומר, אבל קלה מדי אפילו לבגרות(בהנחה שהבנתי אותה נכון):
המהירות היא 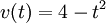 ולכן האינטגרל הוא
ולכן האינטגרל הוא 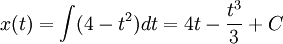 , ועם תנאי ההתחלה
, ועם תנאי ההתחלה 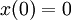 נקבל
נקבל 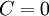 .
.
לכן אנו מעוניינים במקסימום הגלובלי של 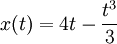 בתחום
בתחום ![[0,3]](/images/math/e/d/9/ed9c05fe24c0f49f5d73f494a921e0c4.png) .
.
הנגזרת שווה למהירות, והיא מתאפסת בתחום הנ"ל בנקודה 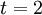 . לכן מספיק למצוא את הערך הגדול ביותר בין הערכים שהפונ' מקבלת בנקודות 2,0,3.
. לכן מספיק למצוא את הערך הגדול ביותר בין הערכים שהפונ' מקבלת בנקודות 2,0,3.
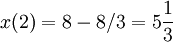 ,
, 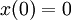 ,
, 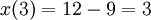 ולכן ההעתק המקסימלי הוא
ולכן ההעתק המקסימלי הוא 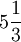 .
.