הבדלים בין גרסאות בדף "פתרון אינפי 1, תש"נ"
מתוך Math-Wiki
(יצירת דף עם התוכן "==שאלה 1== טענה 7.8 אצל ד"ר שיין: תהי <math>f </math> פונקצ' המוגדרת בסביבת <math>x_0</math>. נניח כי <math>f</math> ...") |
|||
| שורה 1: | שורה 1: | ||
| + | ([http://u.cs.biu.ac.il/~sheinee/tests/math/88132/4ef19f65ab044.pdf המבחן] ) | ||
| + | |||
| + | |||
==שאלה 1== | ==שאלה 1== | ||
| − | טענה 7.8 אצל ד"ר שיין: תהי <math>f </math> פונקצ' המוגדרת בסביבת <math>x_0</math>. נניח כי <math>f</math> גזירה ב-<math>x_0</math> וגם <math>f'(x_0) \neq 0</math> וגם קיימת הפונקצייה ההפוכה <math>f^{-1}</math> ורציפה בנקודה <math>y_0=f(x_0)</math>. אזי <math>f^{-1}</math> גזירה ב-<math>y_0 </math>, ונגזרתה שם שווה ל- <math>\frac{1}{f'(x_0)}</math>. | + | (טענה 7.8 אצל ד"ר שיין:) תהי <math>f </math> פונקצ' המוגדרת בסביבת <math>x_0</math>. נניח כי <math>f</math> גזירה ב-<math>x_0</math> וגם <math>f'(x_0) \neq 0</math> וגם קיימת הפונקצייה ההפוכה <math>f^{-1}</math> ורציפה בנקודה <math>y_0=f(x_0)</math>. אזי <math>f^{-1}</math> גזירה ב-<math>y_0 </math>, ונגזרתה שם שווה ל- <math>\frac{1}{f'(x_0)}</math>. |
הוכחה: לפי ההנחה, f גזירה ב-<math>x_0</math> ולכן עפ"י ההגדרה מתקיים <math>\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0)</math>. | הוכחה: לפי ההנחה, f גזירה ב-<math>x_0</math> ולכן עפ"י ההגדרה מתקיים <math>\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0)</math>. | ||
| שורה 7: | שורה 10: | ||
לפי כללי האריתמטיקה (חשבון) של גבולות, מתקיים: <math>\frac{1}{\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}}=\lim_{x\rightarrow x_0}\frac{x-x_0}{f(x)-f(x_0)}=\frac{1}{f'(x_0)}</math>. | לפי כללי האריתמטיקה (חשבון) של גבולות, מתקיים: <math>\frac{1}{\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}}=\lim_{x\rightarrow x_0}\frac{x-x_0}{f(x)-f(x_0)}=\frac{1}{f'(x_0)}</math>. | ||
| − | לפי ההנחות <math>f^{-1}</math> | + | לפי ההנחות <math>f^{-1}</math> רציפה ב<math>y_0</math>. לכן <math>\lim_{y\rightarrow y_0}f^{-1}(y)=f^{-1}(y_0)=x_0</math>, ובאותו האופן <math>\lim_{x\rightarrow x_0}\frac{x-x_0}{f(x)-f(x_0)}=\lim_{y\rightarrow y_0}\frac{f^{-1}(y)-f^{-1}(y_0)}{y-y_0}</math>, ולכן בסך הכל קיבלנו ש- |
| + | |||
| + | <math>\lim_{y\rightarrow y_0}\frac{f^{-1}(y)-f^{-1}(y_0)}{y-y_0}=\frac{1}{f'(x_0)}</math> | ||
| + | זה נותן את הנדרש עפ"י הגדרת הנגזרת. | ||
==שאלה 2== | ==שאלה 2== | ||
| + | |||
| + | נגדיר פונ' <math>h</math> על ידי <math>\forall x \in [0,2]: h(x)=f(x)-\frac{1}{x}</math>. | ||
==שאלה 3== | ==שאלה 3== | ||
גרסה מ־13:09, 3 בפברואר 2012
(המבחן )
שאלה 1
(טענה 7.8 אצל ד"ר שיין:) תהי  פונקצ' המוגדרת בסביבת
פונקצ' המוגדרת בסביבת  . נניח כי
. נניח כי  גזירה ב-
גזירה ב- וגם
וגם 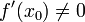 וגם קיימת הפונקצייה ההפוכה
וגם קיימת הפונקצייה ההפוכה 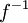 ורציפה בנקודה
ורציפה בנקודה 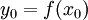 . אזי
. אזי 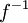 גזירה ב-
גזירה ב-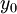 , ונגזרתה שם שווה ל-
, ונגזרתה שם שווה ל- 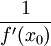 .
.
הוכחה: לפי ההנחה, f גזירה ב- ולכן עפ"י ההגדרה מתקיים
ולכן עפ"י ההגדרה מתקיים 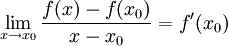 .
.
לפי כללי האריתמטיקה (חשבון) של גבולות, מתקיים: 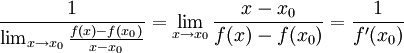 .
.
לפי ההנחות 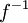 רציפה ב
רציפה ב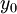 . לכן
. לכן 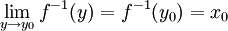 , ובאותו האופן
, ובאותו האופן 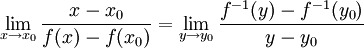 , ולכן בסך הכל קיבלנו ש-
, ולכן בסך הכל קיבלנו ש-
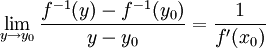 זה נותן את הנדרש עפ"י הגדרת הנגזרת.
זה נותן את הנדרש עפ"י הגדרת הנגזרת.
שאלה 2
נגדיר פונ' 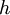 על ידי
על ידי ![\forall x \in [0,2]: h(x)=f(x)-\frac{1}{x}](/images/math/d/e/2/de240f6eefb9356c2d4119ab6a3d415a.png) .
.