הבדלים בין גרסאות בדף "פתרון אינפי 1, תש"נ"
יהודה שמחה (שיחה | תרומות) מ |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 1: | שורה 1: | ||
[[קטגוריה:פתרון מבחנים]][[קטגוריה:אינפי]] | [[קטגוריה:פתרון מבחנים]][[קטגוריה:אינפי]] | ||
([http://u.cs.biu.ac.il/~sheinee/tests/math/88132/4ef19f65ab044.pdf המבחן] ) | ([http://u.cs.biu.ac.il/~sheinee/tests/math/88132/4ef19f65ab044.pdf המבחן] ) | ||
| − | |||
==שאלה 2== | ==שאלה 2== | ||
| − | נגדיר פונקציה <math>h</math> על-ידי <math>\forall x \in [0,2]: h(x)=x\cdot f(x)</math> . | + | נגדיר פונקציה <math>h</math> על-ידי <math>\forall x\in[0,2]:h(x)=x\cdot f(x)</math> . <math>h</math> רציפה בקטע הנ"ל כמכפלת 2 פונקציות רציפות. |
| − | <math>h</math> רציפה בקטע הנ"ל כמכפלת 2 פונקציות רציפות. | + | |
| − | <math>h(2)=2f(2)=2\cdot 1=2</math> ואילו <math>h(0)=0f(0)=0</math> ולכן לפי משפט ערך הביניים <math>\exists x_0 \in [0,2]:h(x)=1</math>. | + | <math>h(2)=2f(2)=2\cdot 1=2</math> ואילו <math>h(0)=0f(0)=0</math> ולכן לפי משפט ערך הביניים <math>\exists x_0\in[0,2]:h(x)=1</math> . |
בנקודה זו מתקיים הדרוש - <math>h(x)=x_0\cdot f(x_0)=1\to f(x_0)=\frac1{x_0}</math> . מש"ל. | בנקודה זו מתקיים הדרוש - <math>h(x)=x_0\cdot f(x_0)=1\to f(x_0)=\frac1{x_0}</math> . מש"ל. | ||
==שאלה 3== | ==שאלה 3== | ||
| − | א) משפט טיילור - תהי <math>f</math> פונקציה מוגדרת וגזירה <math>n+1</math> פעמים בסביבה <math>S</math> של <math>x_0</math> . אז <math>\forall x \in S: f(x)=P_n(x)+R_n(x)</math> , כאשר <math>P_n(x)=\sum\limits_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k</math>. | + | א) משפט טיילור - תהי <math>f</math> פונקציה מוגדרת וגזירה <math>n+1</math> פעמים בסביבה <math>S</math> של <math>x_0</math> . אז <math>\forall x\in S:f(x)=P_n(x)+R_n(x)</math> , כאשר <math>P_n(x)=\sum\limits_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k</math> . |
| − | ב)תהי <math>f(x)=x^3-4x^2+2x</math>. אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נפתור בכל זאת: | + | ב)תהי <math>f(x)=x^3-4x^2+2x</math> . אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נפתור בכל זאת: |
נחשב נגזרות - <math>f'(x)=(x^3-4x^2+2x)'=3x^2-8x+2</math> | נחשב נגזרות - <math>f'(x)=(x^3-4x^2+2x)'=3x^2-8x+2</math> | ||
| שורה 26: | שורה 24: | ||
<math>P_5(x)=\sum_{k=0}^{5}\frac{f^{(k)}(2)}{k!}(x-2)^k=f(2)+f'(2)(x-2)+\frac{f''(2)}{2}(x-2)^2+\frac{f'''(2)}{6}(x-2)^3+0+0=</math> | <math>P_5(x)=\sum_{k=0}^{5}\frac{f^{(k)}(2)}{k!}(x-2)^k=f(2)+f'(2)(x-2)+\frac{f''(2)}{2}(x-2)^2+\frac{f'''(2)}{6}(x-2)^3+0+0=</math> | ||
| − | <math>=2^3-4\ | + | <math>=2^3-4\cdot4+4+(3\cdot4-8\cdot2+2)(x-2)+\frac{(12-8)}{2}(x-2)^2+\frac{6}{6}(x-2)^3</math> |
<math>P_5(x)=-4-2(x-2)+2(x-2)^2+(x-2)^3</math> , | <math>P_5(x)=-4-2(x-2)+2(x-2)^2+(x-2)^3</math> , | ||
| שורה 35: | שורה 33: | ||
==שאלה 4== | ==שאלה 4== | ||
| − | הפונקציה בכל מחזור <math>\pi</math> תעלה בדיוק ב- <math>\pi</math> , ולכן הפונקציה היא אוסף עותקים עולים ('קופצים') ב<math>\pi</math> בכל פעם של קטע בודד באורך <math>\pi</math> שלה. (ראו הגרף) | + | הפונקציה בכל מחזור <math>\pi</math> תעלה בדיוק ב- <math>\pi</math> , ולכן הפונקציה היא אוסף עותקים עולים ('קופצים') ב- <math>\pi</math> בכל פעם של קטע בודד באורך <math>\pi</math> שלה. (ראו הגרף) |
נימוק פורמלי: <math>f(x+\pi)=x+\pi+\sin(2x+2\pi)=x+\sin(2x)+\pi=f(x)+\pi</math> . | נימוק פורמלי: <math>f(x+\pi)=x+\pi+\sin(2x+2\pi)=x+\sin(2x)+\pi=f(x)+\pi</math> . | ||
| שורה 43: | שורה 41: | ||
נגזור: <math>f'(x)=1+2\cos(2x)=0\iff \cos(2x)=-\frac12</math> | נגזור: <math>f'(x)=1+2\cos(2x)=0\iff \cos(2x)=-\frac12</math> | ||
| − | <math>\iff 2x=\frac{2\pi}{3}+2\pi k \ \ | + | <math>\iff 2x=\frac{2\pi}{3}+2\pi k\ \or 2x=-\frac{2\pi}{3}+2\pi k\iff x=\frac{\pi}{3}+\pi k\or x=-\frac{\pi}{3}+\pi k\ (k\in\N)</math> |
זה סיזיפי, אבל מוצאים אילו מהנקודות הנ"ל הן בתחום, מציבים בנגזרת השניה לבדיקת סוג קיצון וכו'. | זה סיזיפי, אבל מוצאים אילו מהנקודות הנ"ל הן בתחום, מציבים בנגזרת השניה לבדיקת סוג קיצון וכו'. | ||
גרסה מ־13:06, 4 בנובמבר 2016
(המבחן )
שאלה 2
נגדיר פונקציה 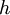 על-ידי
על-ידי ![\forall x\in[0,2]:h(x)=x\cdot f(x)](/images/math/9/6/e/96ef7d073431e82e2662beec4282d710.png) .
. 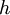 רציפה בקטע הנ"ל כמכפלת 2 פונקציות רציפות.
רציפה בקטע הנ"ל כמכפלת 2 פונקציות רציפות.
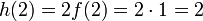 ואילו
ואילו 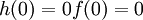 ולכן לפי משפט ערך הביניים
ולכן לפי משפט ערך הביניים ![\exists x_0\in[0,2]:h(x)=1](/images/math/d/4/6/d46e7a1e6045c35f1d8c07e2050f9339.png) .
.
בנקודה זו מתקיים הדרוש - 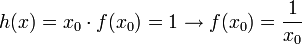 . מש"ל.
. מש"ל.
שאלה 3
א) משפט טיילור - תהי  פונקציה מוגדרת וגזירה
פונקציה מוגדרת וגזירה  פעמים בסביבה
פעמים בסביבה 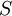 של
של  . אז
. אז 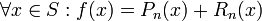 , כאשר
, כאשר 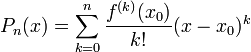 .
.
ב)תהי 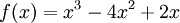 . אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נפתור בכל זאת:
. אנחנו יודעים שפיתוח טיילור של פולינום עבור סדר גדול מדרגתו או שווה לו יהיה שווה לפולינום עצמו, ולכן התרגיל די מיותר, אבל נפתור בכל זאת:
נחשב נגזרות - 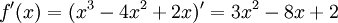
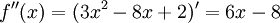
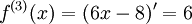
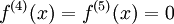
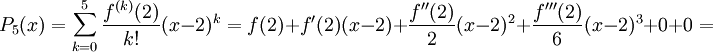
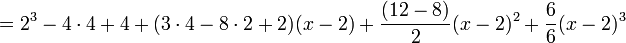
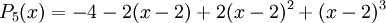 ,
,
ועם קצת פתיחת סוגריים ופישוט נקבל את הפולינום שהתחלנו ממנו.
מתקיים 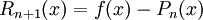 ולכן השארית היא
ולכן השארית היא  , כצפוי.
, כצפוי.
שאלה 4
הפונקציה בכל מחזור 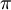 תעלה בדיוק ב-
תעלה בדיוק ב- 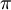 , ולכן הפונקציה היא אוסף עותקים עולים ('קופצים') ב-
, ולכן הפונקציה היא אוסף עותקים עולים ('קופצים') ב- 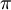 בכל פעם של קטע בודד באורך
בכל פעם של קטע בודד באורך 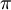 שלה. (ראו הגרף)
שלה. (ראו הגרף)
נימוק פורמלי: 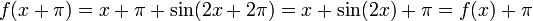 .
.
גם ברור שהיא רציפה כסכום והרכבת רציפות.
נגזור: 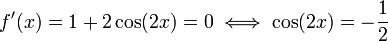
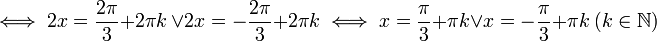
זה סיזיפי, אבל מוצאים אילו מהנקודות הנ"ל הן בתחום, מציבים בנגזרת השניה לבדיקת סוג קיצון וכו'.
גרף באדיבות וולפראם: קובץ:X+sin2x.pdf
שאלה 5
א) סדרה ממשית 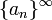 תקרא סדרת קושי אם("ם):
תקרא סדרת קושי אם("ם):
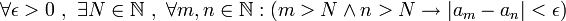
ב) ניקח את הסדרה  שהאיבר ה-
שהאיבר ה-  -י בה הוא הקירוב העשרוני עד למקום ה-
-י בה הוא הקירוב העשרוני עד למקום ה-  של
של 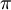 (יותר מגניב משורש 2, אבל פחות נכון כי לך תוכיח שהוא לא-רציונאלי).
היא של רציונאליים, היא מתכנסת מעל הממשיים ולכן היא סדרת קושי, אבל
(יותר מגניב משורש 2, אבל פחות נכון כי לך תוכיח שהוא לא-רציונאלי).
היא של רציונאליים, היא מתכנסת מעל הממשיים ולכן היא סדרת קושי, אבל 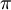 , אם להאמין לספרים, אינו רציונאלי.
, אם להאמין לספרים, אינו רציונאלי.
ג) נשים לב שהטור 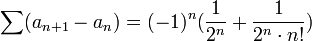
שאלה 6
השאלה אמנם לא בחומר, אבל קלה מדי אפילו לבגרות(בהנחה שהבנתי אותה נכון):
המהירות היא 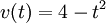 ולכן האינטגרל הוא
ולכן האינטגרל הוא 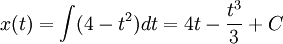 , ועם תנאי ההתחלה
, ועם תנאי ההתחלה 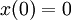 נקבל
נקבל 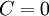 .
.
לכן אנו מעוניינים במקסימום הגלובלי של 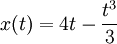 בתחום
בתחום ![[0,3]](/images/math/e/d/9/ed9c05fe24c0f49f5d73f494a921e0c4.png) .
.
הנגזרת שווה למהירות, והיא מתאפסת בתחום הנ"ל בנקודה 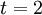 . לכן מספיק למצוא את הערך הגדול ביותר בין הערכים שהפונקציה מקבלת בנקודות 2,0,3.
. לכן מספיק למצוא את הערך הגדול ביותר בין הערכים שהפונקציה מקבלת בנקודות 2,0,3.
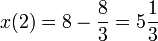 ,
, 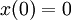 ,
, 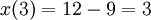 ולכן ההעתק המקסימלי הוא
ולכן ההעתק המקסימלי הוא 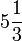 .
.